解答题1:求积分与极限

- 别跳步*,推理思路get
- 积分与求导的联系
- 注意:
注意事项:带有负号的换元积分的变换
10.
12. 注意:当被积函数中存在积分变量与求导变量时,要换元
13. 求驻点,极值点(可不求,因为驻点是所有可能的极值点),求边界点,对比值判断。
15.
17. (不跳步提高做题准确性)
- 收敛设为常数
- 凑积分

分部积分的思路(√)
分析规律(courage)
(1)求递推的关系,找到n和n-1的关系
(2)ing:线索:找到复合函数的原函数的影子。
解答题2:几何运用

- 旋转体体积
(1)(2) again
(慢到你能反应过来的速度)
31.求面积
32. 曲线积分
- 换元积分求导
- 曲线积分公式
- 注意题中的积分上限和y的取值范围不是一回事。
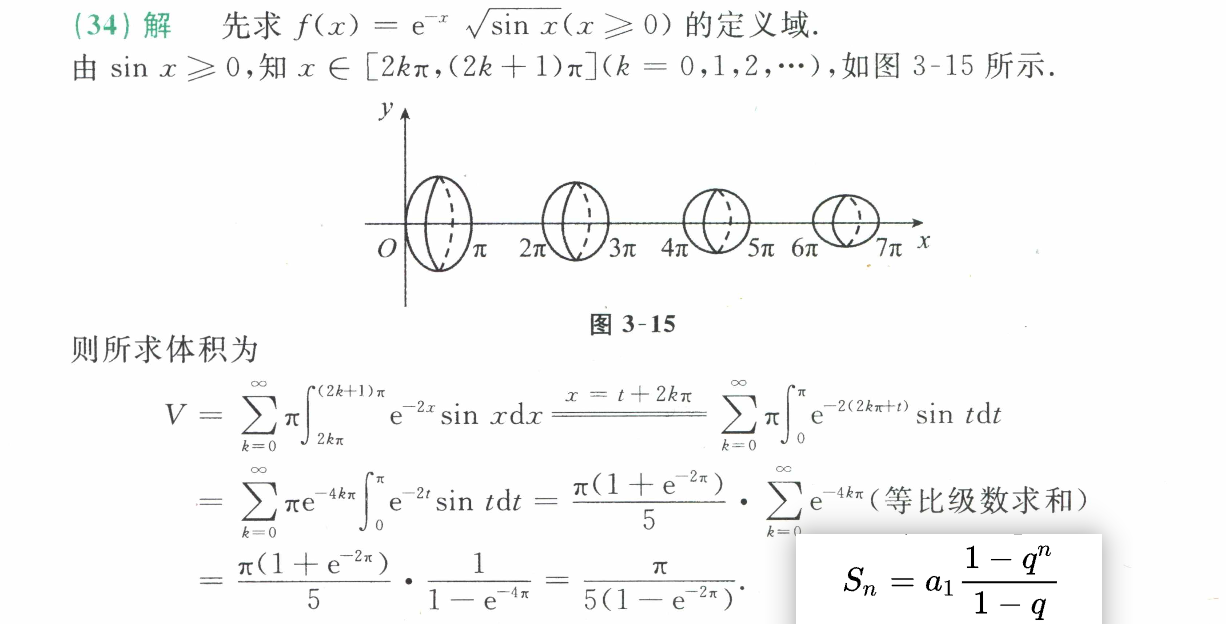
34.旋转体体积
1. e和三角函数,分部积分求两次,即可求出原式
2.等比公式
1.绕x、y轴的体积公式
2.华里士公式,偶数项的公式,奇数项的推导,从2π推导到π/2。
36.
(学会观察)
37.
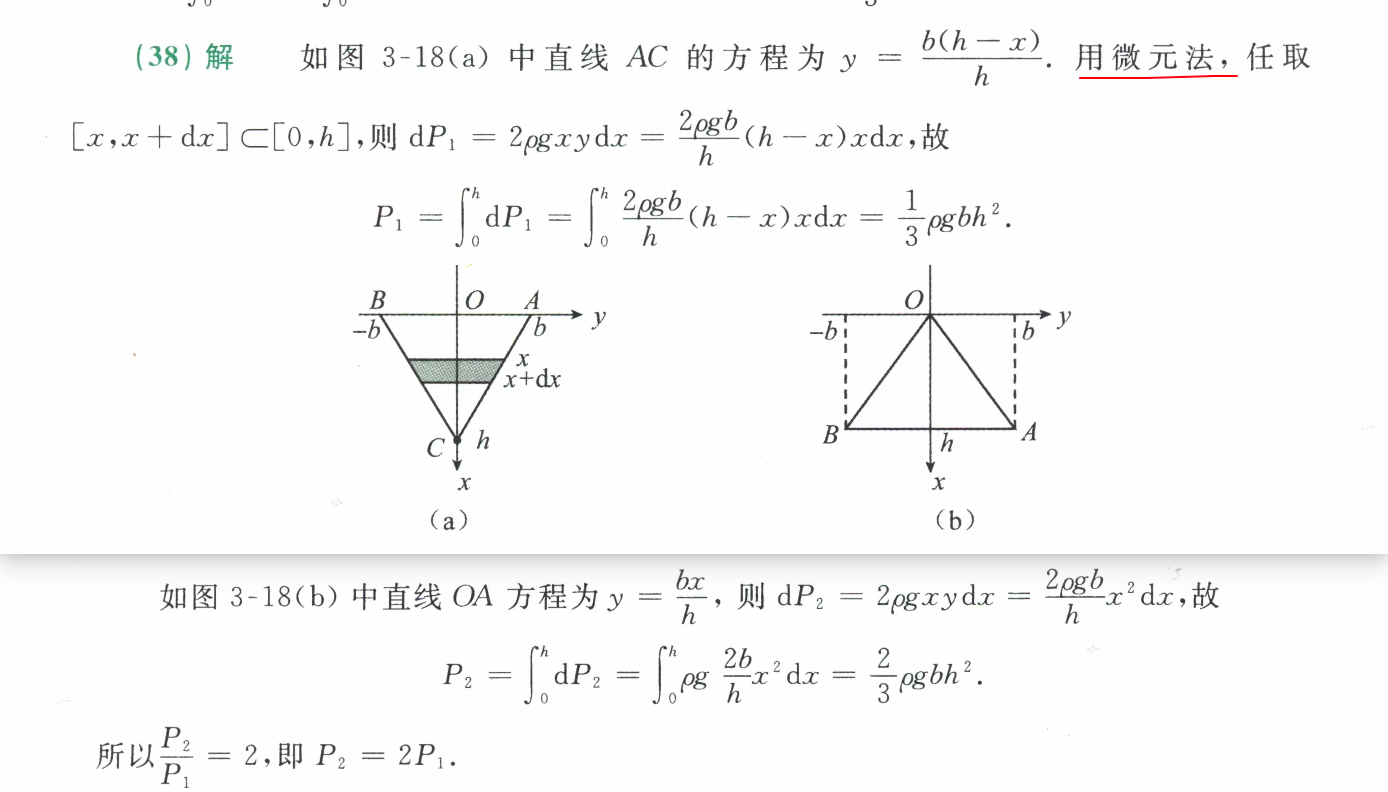
38.对。

极坐标与参数方程的变换
简化的思路:去掉绝对值。
41. 极坐标变参数方程
42.
44.公式计算:华里士公式的特例
46.积分上下限选取的技巧
利用极坐标公式直接求
答案不对?
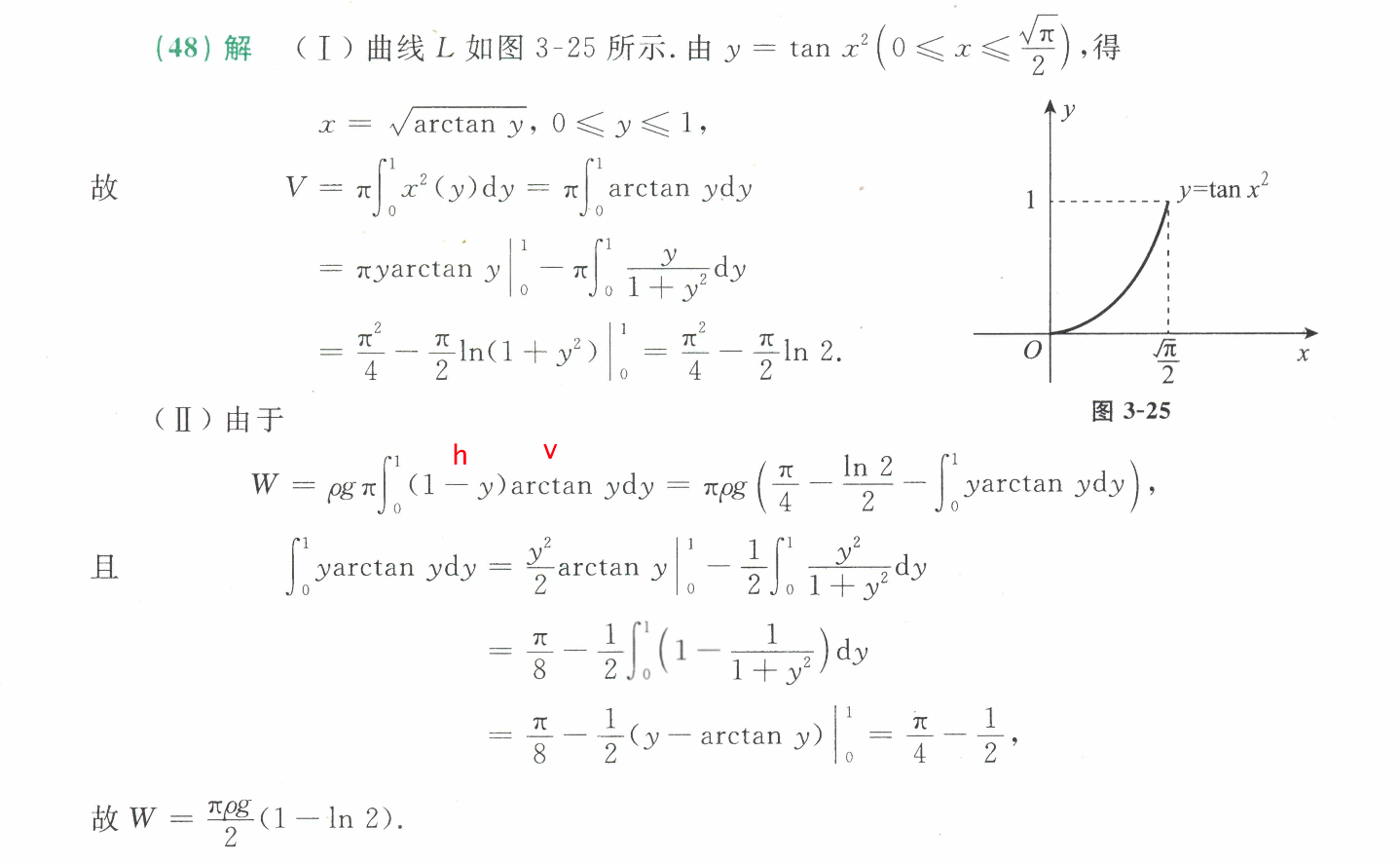
48. again
沿着y积分,简化思路:反函数
拓展题
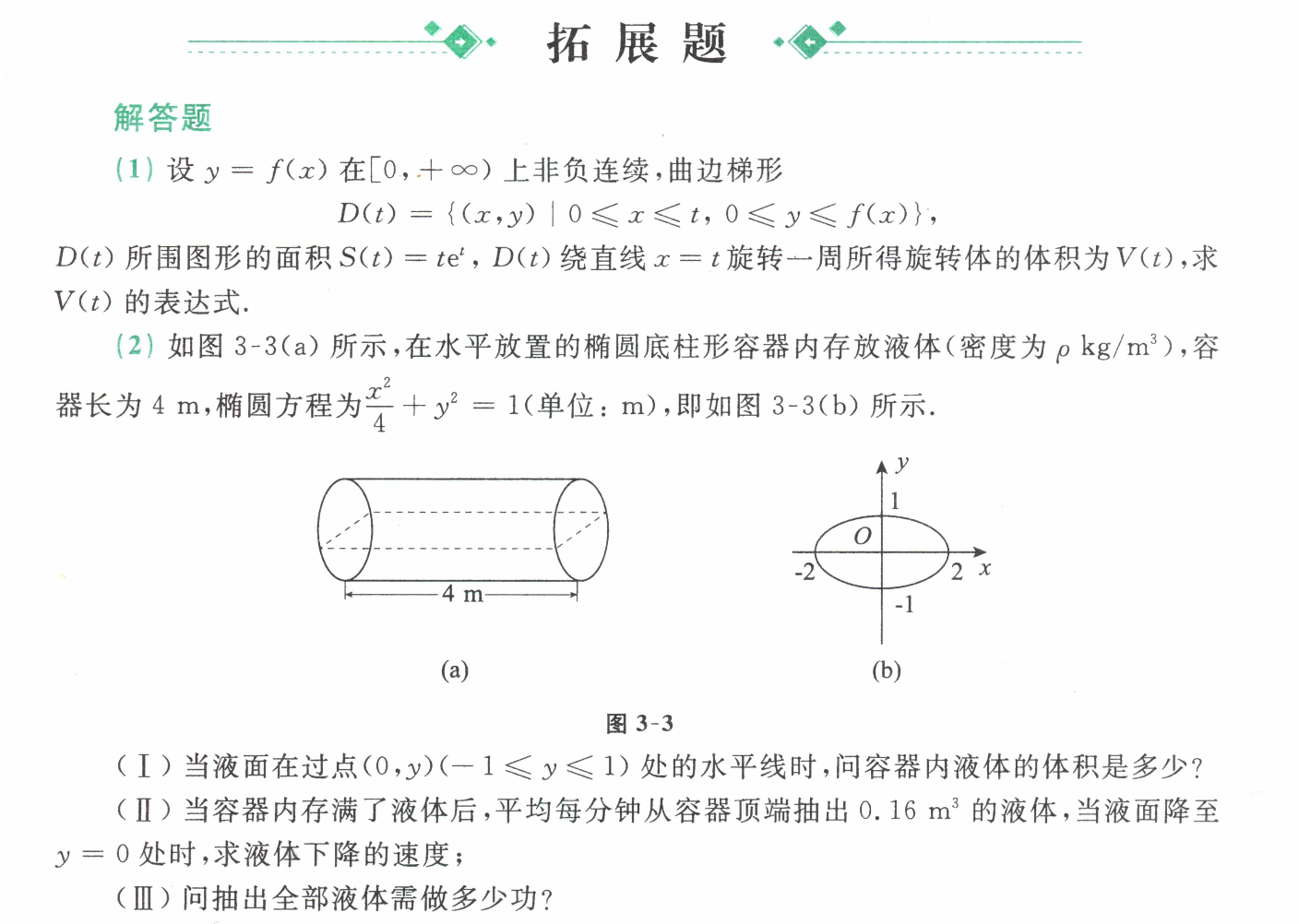
- 求体积
(1):选y为积分方向,简化积分
(2):先按照定义求速度,然后再复合函数求导
(3)选y为积分方向。
得分注意事项
- 计算不跳步
- 公式、解题方法总结。




















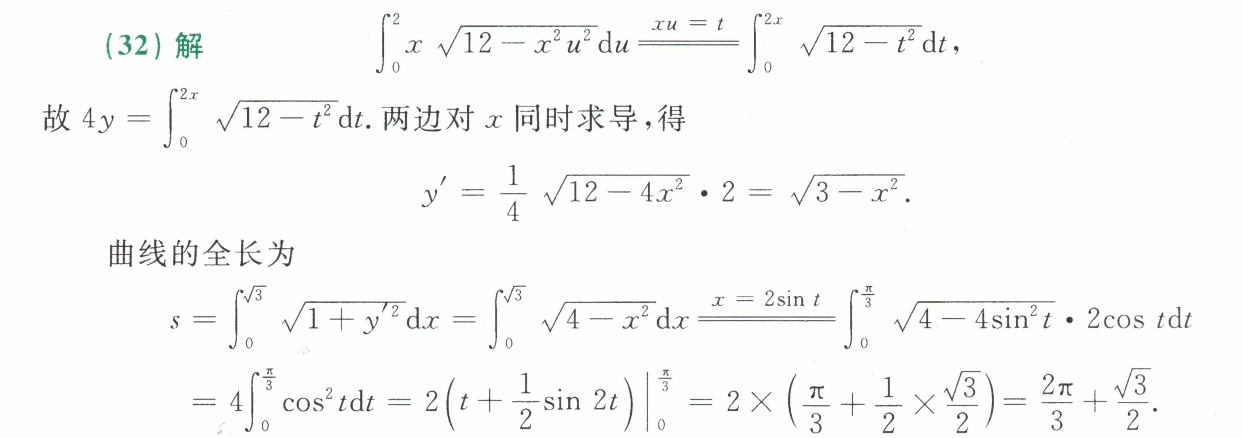







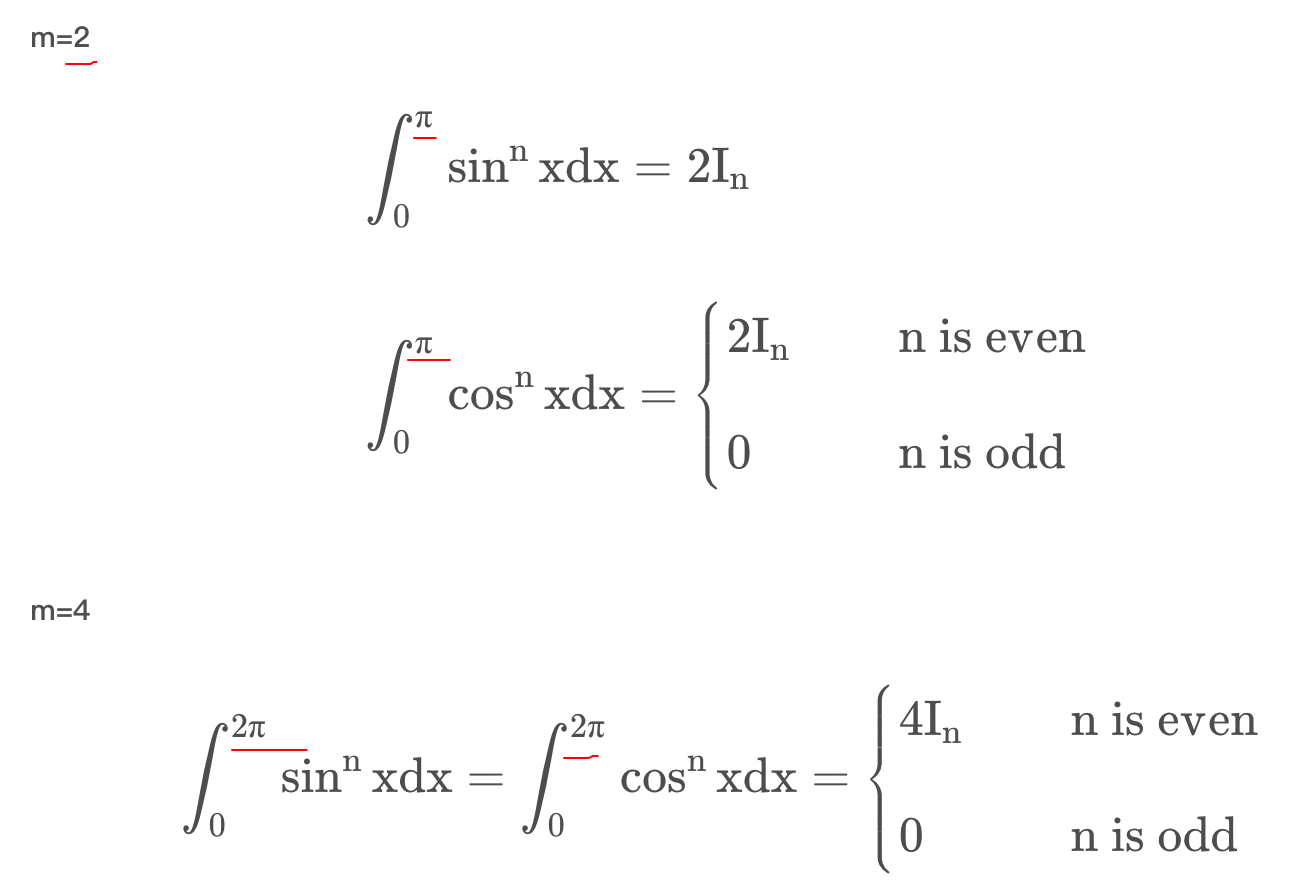



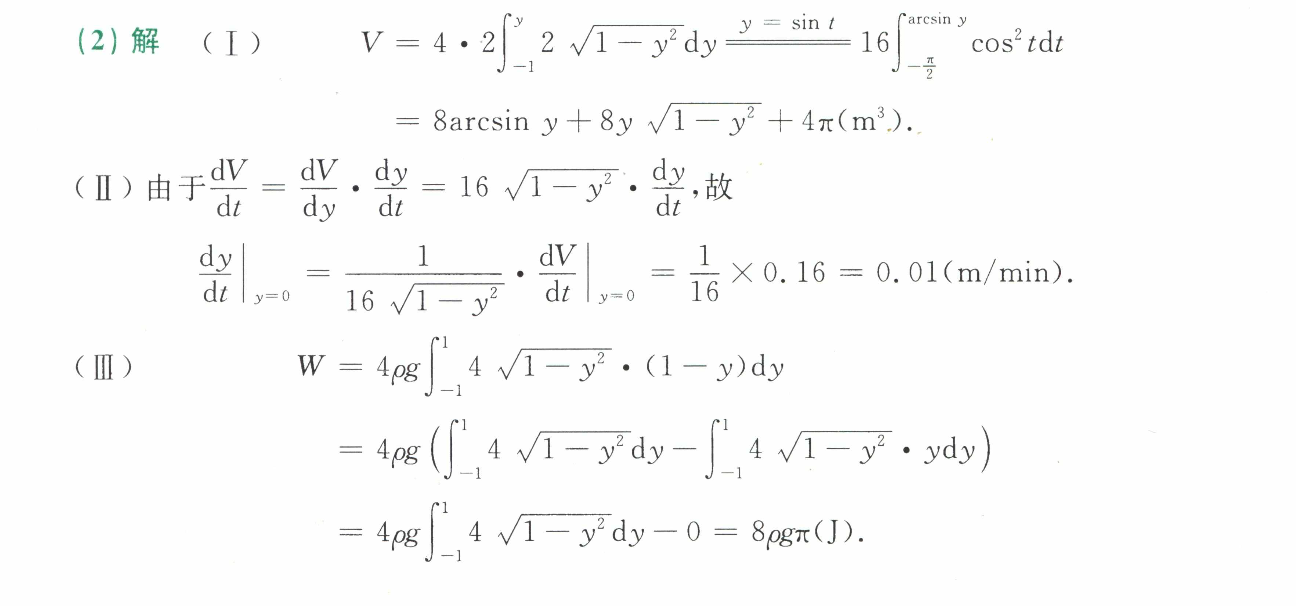


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










