原文:Uhlmann, Markus. “An immersed boundary method with direct forcing for the simulation of particulate flows.” Journal of computational physics 209.2 (2005): 448-476.
概述
使用固定且均匀的计算网格来计算悬浮刚性颗粒周围的不可压缩粘性流
主要思想是将 Peskin 的正则化 delta 函数方法 [Acta Numerica 11 (2002) 1] 纳入流固相互作用力的直接公式中,以便允许欧拉和拉格朗日表示之间的平滑转换,同时避免时间步长的严格限制。该技术是在有限差分和分数步环境中实现的。
引言
处理悬浮颗粒计算的一种方法是在与固体物体界面处无滑移条件下求解瞬态流体域中的纳维-斯托克斯方程。然而,这意味着在模拟过程中使网格适应粒子的不同位置,并导致大量的计算成本。这种技术的一个例子是 Hu 等人的任意拉格朗日-欧拉粒子移动器。 [3]已成功应用于各种沉降问题
为啥这意味着在模拟过程中使网格适应粒子的不同位置?
这应该一开始就不是说的固定欧拉网格的思路,而是一开始就是默认要创建一个贴体网格来求解
为了避免频繁的重新划分网格,可以在固定网格上求解流动方程,同时通过添加到纳维-斯托克斯方程中的适当公式化的源项来强加固体的存在。这类技术被称为“虚拟域方法”。 Peskin 的浸没边界 (IB) 方法是其先驱之一,最初是为柔性膜周围的流动而设计的,特别是人类心脏中的流动 [10]。基本思想是确定任意(拉格朗日)位置处的奇异力分布,并通过正则化狄拉克δ函数将其应用于固定参考系中的流动方程。同时,膜以局部流速移动。该问题的附加力项只是膜变形及其弹性特性的函数。 Peskin δ 函数的精心设计对该方法的效率至关重要
在参考文献[12,4,9]以及相关研究[13,14]中,奇异力是通过Goldstein等人首先提出的反馈机制获得的。 [15]并被称为“虚拟边界法”。其中,与速度(或位置)的局部期望值的偏差会产生相反方向的力,该力倾向于恢复目标值。换句话说,虚拟弹簧和阻尼器系统连接到虚拟边界点,局部强制执行预定行为。这种流固相互作用力的间接公式的一个不良特征是引入了额外的自由参数。在实践中,弹簧刚度和阻尼常数的值需要根据问题来确定。此外,需要解决弹簧阻尼系统振荡的特征时间尺度,这可能导致时间步长受到严格限制[12,14]
为了避免虚拟边界力的弊端,Fadlun 等人。 [16]引入了力项的直接公式。粗略地说,该方法包括修改离散动量方程的隐式矩阵的条目,以便在每个时间步后获得边界点处的所需速度。作者证明该方案不受虚拟边界方法的时间步长限制。
modifying the entries of the implicit matrix of the discretized momentum equation
其中这个 entries 翻译成条目,怎么看上去这么怪
感觉翻译成元素更好
The numbers, symbols or expressions in the matrix are called its entries or its elements
金等人。 [5]后来提出了上述直接强迫方法的显式变体,它允许保持标准有限差分方法的原始简单矩阵结构。
在这两个参考文献 [16,5] 中,目标都是复杂域中流的有效计算。尽管法德伦等人。 [16]提出了一个涉及移动边界的流动的例子,但没有证明相对运动期间边界力的平滑性。后来人们认识到,将固定网格节点处的值和任意位置边界处的值相关联的插值程序可能会导致力振荡,这对于颗粒流模拟的目的来说是不希望的[17]
Kajishima 和 Takiguchi [6] 使用一种极其简单的方案来模拟流固相互作用。在时间步结束时,速度被明确设置为每个固体子域内粒子的刚体速度。
该方法使用每个计算单元的固体体积分数作为权重因子,将界面、流体和固体速度平滑地连接起来。该方法非常有效,可以在颗粒雷诺数为 350 时对 Oð1000Þ 颗粒的沉降进行长时间积分。尽管这种策略避免了作用在粒子上的水动力的虚假振荡,但该力仍然表现出很强的网格依赖性[17]。此外,应该提到的是,所得的流场并不能验证颗粒附近的无发散条件。
Glowinski 等人采取了不同的方法。 [18]他们在有限元环境中通过拉格朗日乘子技术将刚体运动施加到粒子占据的区域上。在随后的模拟中,Glowinski 等人。 [7]使用一阶精确的四步算子分割方案进行时间离散化,包括更新粒子位置时减少局部时间步长。该方法适用于各种沉降问题 [7] 以及狭窄间隙中 Oð1000Þ 球体的流化 [19]。然而,应该记住,使用基于四面体单元的网格系统可能会破坏问题的固有对称性。帕坦卡等人。 [20]提出了一种相关的拉格朗日乘子技术,其中变形率张量而不是速度被施加在粒子子域中,从而简化了不规则形状粒子的处理。 Patankar [21] 提出了进一步的改进,他展示了如何在施加刚性约束时消除迭代过程的需要。在审查过程中,我们注意到该方案同时在控制体积环境中实现了[22],并成功应用于颗粒流的 DNS
最后,应该提到的是,Zhang 和 Prosperetti [8] 最近提出了一种基于球形粒子附近局部斯托克斯动力学的半解析方法。与外部(纳维-斯托克斯)解的匹配是迭代执行的。然而,到目前为止,这些作者只报道了二维沉降问题的计算。
目前工作的目标是开发一种虚拟域方法,其中强迫项不是通过任何类型的反馈机制获得的,并且尽可能地抑制固定网格引起的振荡。我们将提出一种策略,一方面,将原始 IB 方法在拉格朗日和欧拉位置之间平滑传递物理量 quantities 的能力,另一方面,与直接、明确地表述流固相互作用力的优点结合起来。因此,本方法比现有的直接方法产生更小的振荡粒子力,并且与间接方法相比产生更高的效率。
问题表述
不可压流的 NS 方程

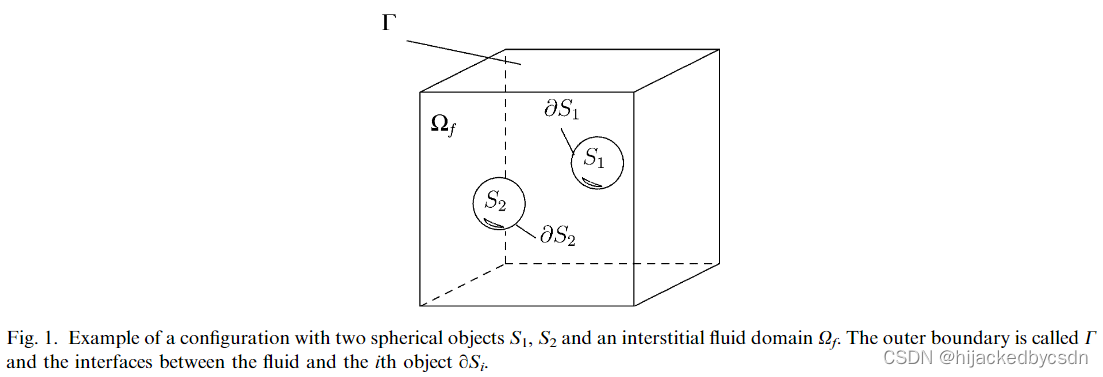
其中 u 是流体速度矢量,p 是用流体密度标准化的压力,f 是体积力项。这些方程在整个域 X 中强制执行,包括实际流体域 Ω f \Omega_f Ωf 和 Np 个悬浮固体物体占据的空间 ∪ i = 1 N p S i \cup_{i=1}^{N_p}S_i ∪i=1NpSi(参见图 1)。在第 3 节中,力项 f 将以这样的方式表述,以表示固体对流体的作用
除了提供适当的初始条件和外边界C条件外,我们还需要描述悬浮颗粒在重力和水动力作用下的运动。该主题将在第 4 节中讨论
固体对流体的作用
欧拉和拉格朗日变量的空间离散
固定笛卡尔网格 g h g_h gh
它由固定的网格点 x i j k = ( i , j , k ) h \mathrm{x}_{ijk} = (i,j,k)h xijk=(i,j,k)h 组成
覆盖了域 Ω \Omega Ω
h h h 为网格宽度
嵌入对象被定义为 N L N_L NL 个点
他们的位置可以被定义为

这些点成为拉格朗日力点
为了方便,本论文之后提到个各个物体的 N L N_L NL 都假设相同
位置 X i \mathrm{X}_i Xi 用于插值目的,并且相对于连接到第 i 个粒子的坐标系而言在时间上是恒定的。这个概念与 IB 方法框架中使用的拉格朗日标记点相关[23]。然而,在这个方法中,标记点随局部流体速度平流传播,而我们的(本论文?)拉格朗日力点跟随粒子的刚体运动,因此不需要额外的跟踪,即它们不构成额外的自由度
此外,我们将离散体积 Δ V l ( i ) \Delta V_l^{(i)} ΔVl(i) 与每个力点相关联,以便所有这些体积的联合在每个颗粒周围形成一个薄壳(厚度等于一个网格宽度)。与参考文献 [11,4] 类似,这使我们能够在每个拉格朗日力点处制定体积力,而不是在原始 IB 方法中,在拉格朗日标记点处定义奇异力。出于效率的考虑,这里我们不对粒子内部施加任何力(参见参考文献[4]中的相关讨论)。从颗粒沉降的二维测试计算中,我们可以得出结论,在整个颗粒体积中定位力点不会导致显着不同的结果
在附录 A 中,可以找到与球形粒子和(在二维情况下)圆形物体的力点分布相关的几何定义。尽管此后仅考虑这两种简单形状,但本方法同样适用于任意形状的物体,甚至适用于随时间演变的刚性颗粒表面(例如,由于燃烧过程)
体积力的表述
强制方案的目的是在选定的网格节点处施加所需的速度值。对于一些几何上简单且静止的固体对象,网格节点可以位于界面上,并且强制减少到直接修改相应的矩阵条目,使得局部速度消失。然而,真实的粒子具有与任意的、与时间相关的位置的界面。网格。因此,欧拉位置和拉格朗日位置之间的插值步骤是必要的。
为了讨论一般概念,让我们将时间离散动量方程写成以下形式

其中 r h s n + 1 / 2 \mathrm{rhs}^{n+1/2} rhsn+1/2 在 t n t^n tn 和 t n + 1 t_{n+1} tn+1 之间的某个瞬时重新组合对流、压力和粘性项
这里的 u 应该都是在拉格朗日点?
产生所需速度 u(d) 的力项就简单地表示为 [16]:

该式定义在一些选定的网格节点(其他地方为零)。
金等人。 [5]使用位于浸入物体内部并邻近其界面的网格节点,通过线性插值过程评估所需速度 u(d)。法德伦等人。 [16]讨论了几种相关的插值技术。我们个人的经验是,在物体任意移动的情况下,这些程序可能会由于平滑不足而导致水动力的强烈振荡
作为替代,我们建议使用下式评估拉格朗日力点 X l ( i ) X_l^{(i)} Xl(i) 处的力项

在 (5) 中以及此后,我们使用大写字母来表示在拉格朗日力点 X l ( i ) X_l^{(i)} Xl(i) 位置处计算的量。流体和固体界面上某个位置处的所需速度可以简单地由固体物体的刚体运动给出,如下式
感觉之前的式子里面的小写 u 是拉格朗日坐标里面的,但是现在他又说 (5) 式之后的大写字母才是拉格朗日坐标

u c ( i ) , ω c ( i ) , x c ( i ) u_c^{(i)}, \omega_c^{(i)}, x_c^{(i)} uc(i),ωc(i),xc(i) 是第 i 个固体的平移速度和旋转速度以及中心坐标
(5) 式右侧的剩余两项可以收集为

它对应于在不施加力项的情况下获得的初步速度。它的欧拉对应物

该式在我们的方案中明确可用(参见方程(12a))。
为了完成(3)中强迫项的评估,我们还需要提供一种传递机制,将初速度 ( u ~ , U ~ ) (\widetilde{u}, \widetilde{U}) (u ,U ) 和力 ( F n + 1 / 2 , f n + 1 / 2 ) (F^{n+1/2},f^{n+1/2}) (Fn+1/2,fn+1/2) 在拉格朗日坐标和欧拉坐标之间来回传输
感觉 (5) 之前的式子里面的小写 u 是拉格朗日坐标里面的,现在他说 (5) 式之后的大写字母才是拉格朗日坐标
然后这里的说法,好像“小写-大写”对应“拉格朗日坐标和欧拉坐标”一样,又和 (5) 式的约定冲突了?
拉格朗日位置和欧拉位置之间的物理量 quantities 转移
在这里,我们使用 Peskin [10,23] 引入的正则化 delta 函数类作为拉格朗日和欧拉位置之间转移步骤的内核。为了方便起见,删除时间上标,我们写道:
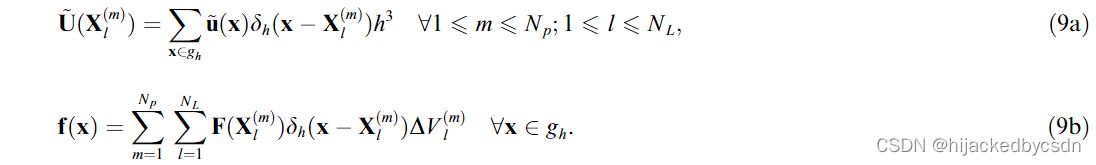
δ h \delta_h δh 内核的显着特性如下
-
δ h \delta_h δh 是一个连续可微的函数,因此它可以产生更平滑的传输,比如相对于线性插值而言。
-
对于平滑场,使用内核 δ h \delta_h δh 进行插值是二阶精确的(参见第 5.1.1 节)。
-
正则化 delta 函数的支持 support 较小,这使得对式(9)中的求和进行评估比较便宜。特别是,我们使用 Roma 等人定义的 δ h \delta_h δh 表达式。 [25],每个坐标方向仅涉及三个网格点。
这里说的 support 应该是内核半径?
- 对于所有真实的位移 shifts X,我们有

这里说的 shifts 虽然是偏移,但是更像是指的是 存在偏移的坐标?或者说是相对于内核中心的位移?
它们是狄拉克 δ 函数基本属性的离散类似物。因此,可以证明 [23] 添加到流体的力和扭矩的总量不会因 (9b) 中的传递步骤而改变,即
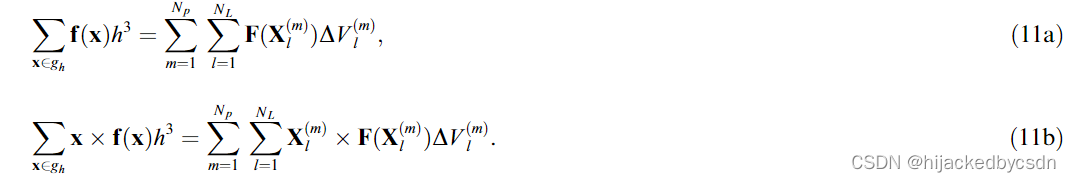
流体求解器
我们的纳维-斯托克斯求解器基于传统的分数步法来增强连续性。对流项采用三步龙格-库塔方案,而粘性项则采用 Crank-Nicholson 方法处理,从而实现整体形式二阶时间精度。
空间导数通过交错网格上的二阶中心有限差分算子进行评估。交错意味着速度 ub 的每个分量都在其自己的欧拉网格位置定义,例如 x ∈ g h ( β ) x \in g_h^{(\beta)} x∈gh(β) 。因此,(9)中的欧拉位置和拉格朗日位置之间的转换需要针对每个分量单独进行。
第 k 个龙格-库塔步骤的离散流动方程(包括流固耦合项)如下:
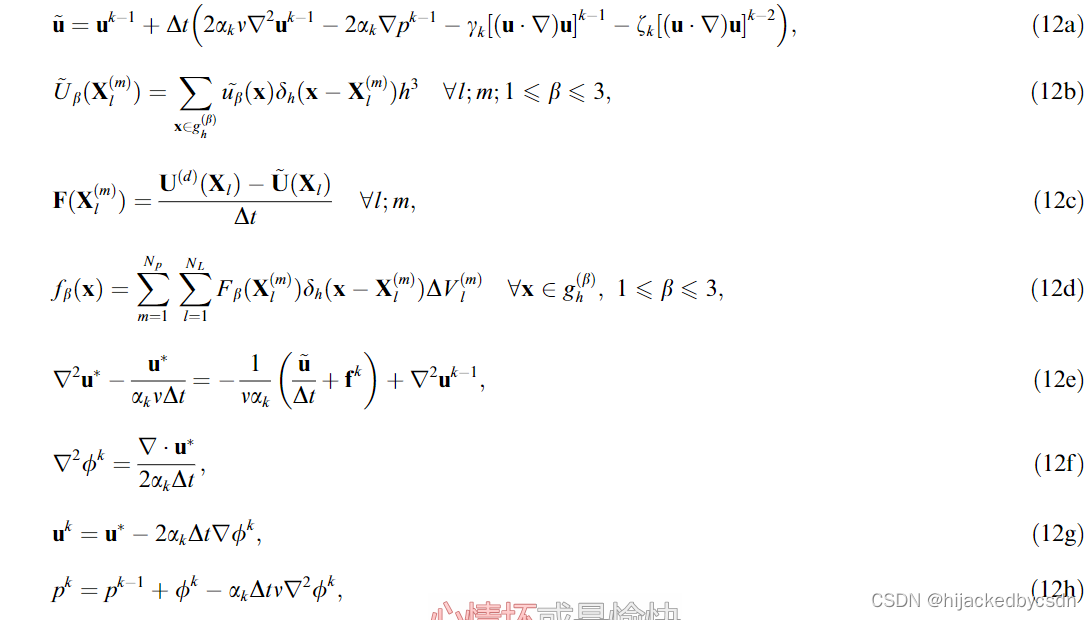
系数 α k , γ k , ζ k , ( 1 ⩽ k ⩽ 3 ) \alpha_k, \gamma_k, \zeta_k, (1 \leqslant k \leqslant 3) αk,γk,ζk,(1⩽k⩽3) 在 [26] 被给出
中间变量 ϕ \phi ϕ 就是所谓的“伪压力”,没有物理意义。等式。 f 设置为零的 (12e)–(12h) 对应于基本的分数步法 [27]。
在周期性边界条件的情况下,出于兼容性原因,需要从动量方程中减去力项的空间平均值 ∫ ω f d x / ∣ ∣ ω ∣ ∣ \int_{\omega} f dx / || \omega || ∫ωfdx/∣∣ω∣∣ [11,4]。
应该指出的是,所得到的速度场 uk 在离散算子的意义上是无散的。正如之前关于耦合力显式公式的研究一样[16],流固耦合对时间步长没有额外的限制。这意味着当 CFL 数的值接近基本龙格-库塔方案所施加的 3 \sqrt 3 3 理论极限时,稳定积分是可能的。
在实践中,亥姆霍兹(12e)和泊松(12f)问题的求解执行如下。在二维空间中,基于循环约简 clic reduction [28] 的直接求解方法用于解决这两类隐式问题。为了在三个空间维度的情况下在多处理器机器上有效实现,亥姆霍兹问题通过二阶精确近似分解来简化,泊松问题通过多重网格技术来解决。
固体粒子的运动
粒子的运动受刚体线性动量和角动量的牛顿方程控制。通过相应流体域上的动量平衡来评估作用在粒子上的流体动力,我们可以这样写
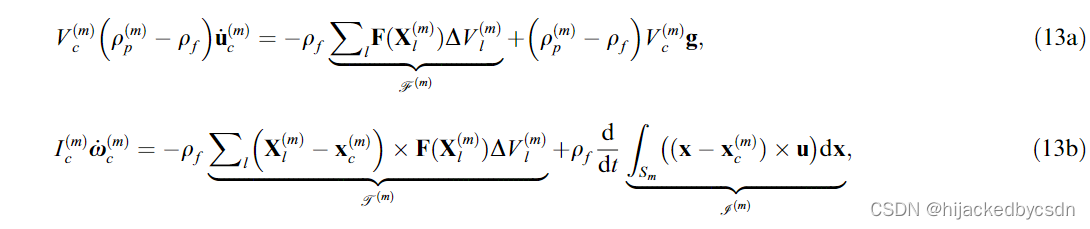
其中 V c ( m ) , I c ( m ) , ρ p ( m ) V_c^{(m)}, I_c^{(m)}, \rho_p^{(m)} Vc(m),Ic(m),ρp(m) 是第 m 个粒子的体积、惯性矩和密度; ρ f \rho_f ρf 是流体密度; g 是重力加速度矢量
(13b)的式子 r.h.s 上的第二项表示占据第m个固体域的流体的角动量的变化率。其贡献是由于仅将流固耦合力施加到每个颗粒的表面会导致颗粒域 Sm 内的流体残留非刚性运动。在实践中,积分 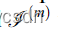 被评估为每个网格单元的总和,其中单元的体积固体分数作为权重。在我们的三维应用中,变化率项是通过假设固体体积内的刚体运动来近似的,即使用方程: (B.4)。这样做是出于效率的原因,第 5.2.2 节给出了理由
被评估为每个网格单元的总和,其中单元的体积固体分数作为权重。在我们的三维应用中,变化率项是通过假设固体体积内的刚体运动来近似的,即使用方程: (B.4)。这样做是出于效率的原因,第 5.2.2 节给出了理由
运动方程 (13) 通过与流体方程相同的龙格-库塔过程在时间上离散化
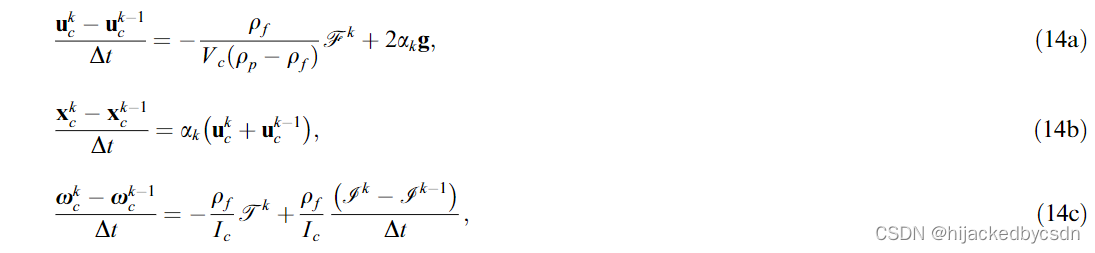
其中我们删除了粒子索引(m)的上标,转而使用龙格-库塔子步索引。另请注意,推进方程不需要角位置。在从完全刚性近似评估变化率项的情况下,方程: (14c) 被替换为

流体和粒子方程的弱耦合
我们的方案包括,
首先,根据先前的龙格-库塔层(level ?)已知的粒子位置和速度,求解流体方程(12),然后使用最新的流场求解所示的粒子方程(14)。
为了简化符号,考虑以下模型系统,其中每个子系统仅包含一个变量,分别为流速 u 和颗粒中心速度 uc

函数
Ψ
1
,
Ψ
2
\Psi_1, \Psi_2
Ψ1,Ψ2 代表各子系统的时间提前量。该模型代表了我们的整个系统,因为它在前一种情况下是隐式的,而在后一种情况下是显式的。两个子系统之间的耦合是显式的,也称为“弱耦合”。
过去已经注意到,对于流体方程与刚性颗粒的运动方程弱耦合的方法来说,非常轻的颗粒的处理存在问题。胡等人。 [3] 显示了在使用完全显式耦合的情况下,在粒子由于重力而从静止加速的情况下,粒子速度的振荡如何根据添加的质量而出现。在实践中,我们发现,对于本方法,流体-颗粒系统的稳定弱耦合积分存在密度比的下限:对于圆盘,qp/qf > 1.05;对于球形颗粒,qp/qf > 1.2。我们观察到,极限值并不显着取决于所选的时间步长。顺便说一句,根据我们的经验,Kajishima 和 Takiguchi [6] 的显式耦合方案允许密度比 qp/qf > 2 (圆盘)。
在弱耦合过程不稳定的情况下,可以对每个龙格-库塔步骤执行类似高斯-赛德尔的子迭代[24]。为了避免与迭代耦合相关的额外开销,完全隐式耦合(如参考文献[21]中提出的方法)原则上是更可取的。这方面留作我们计划的未来扩展。在以下示例中,我们选择了高于指定阈值的密度比。
实验
总结
我们提出了一种改进的浸入边界方法,直接公式化了流固相互作用力。 Peskin [23] 的正则化 delta 函数用于任意拉格朗日位置和离散欧拉位置之间的关联。因此,作用在颗粒上的流体动力没有显着的振荡,允许颗粒平稳运动。另一方面,强制方案的直接(非反馈)特征避免了时间步长的额外限制。
当前的方法是在有限差分和分数步环境中实现的。流体方程与颗粒刚体运动的牛顿方程弱耦合,这对颗粒和流体之间的密度比施加了大约 1.2 的下限,以实现稳定积分。
新方案应用于泰勒-格林流动、固定和摆动圆柱体周围的流动以及二维和三维空间中的沉降问题。通过将我们目前的结果与实验和独立数值模拟的参考值进行比较,我们证明了该方法的高精度。此外,我们使用多处理器机器对真正三维域中的多粒子系统进行的模拟表明,使用当前方法研究大规模配置是可行的。
说实话……不知道怎么把公式和代码对应起来
 用于模拟颗粒流的直接强迫浸没边界法笔记
用于模拟颗粒流的直接强迫浸没边界法笔记





















 5919
5919

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








