这里写目录标题
贝叶斯公式
模型概率的公式
一开始看了这个 https://zhuanlan.zhihu.com/p/98756147
假设模型参数满足一个高斯分布 W ∼ N ( 0 , 1 ) W \sim N(0,1) W∼N(0,1),观测数据集 X , Y X,Y X,Y 然后他介绍了一个公式说是贝叶斯公式:
p ( W ∣ X , Y ) = p ( Y ∣ X , W ) p ( W ) p ( Y ∣ X ) p(W \vert X,Y) = \dfrac{p(Y \vert X,W)p(W)}{p(Y|X)} p(W∣X,Y)=p(Y∣X)p(Y∣X,W)p(W)
我一开始是不知道贝叶斯公式是这个,感觉跟我知道的不一样;然后我还不知道他为什么说似然是 p ( W , X ∣ Y ) p(W, X|Y) p(W,X∣Y),对先验、后验、似然的理解我是看 https://blog.youkuaiyun.com/kww_kww/article/details/52527888 的,所以我就固定死了理解右边分子上的是似然
之后看了别人的文章,也挺多看不懂,但是看到别人提了关键的一句
X 和 W 之间是相互独立的
这之后就好办了
其实我觉得贝叶斯公式本质上就是一个恒等式
p ( X , Y ) = p ( X ∣ Y ) p ( Y ) = p ( Y ∣ X ) p ( X ) p(X,Y) = p(X \vert Y)p(Y) = p(Y \vert X)p(X) p(X,Y)=p(X∣Y)p(Y)=p(Y∣X)p(X)
它的物理意义就是,两个事件同时发生的概率用两种条件概率的计算方法都是一样的
可以写:
p ( X , Y , W ) = p ( W ∣ X , Y ) p ( X , Y ) = p ( Y ∣ X , W ) p ( X , W ) p(X,Y,W) = p(W \vert X,Y)p(X,Y) = p(Y \vert X,W)p(X,W) p(X,Y,W)=p(W∣X,Y)p(X,Y)=p(Y∣X,W)p(X,W)
然后根据隐含条件,X 和 W 是互相独立的,有 P ( X , W ) = p ( X ) p ( W ) P(X,W) = p(X)p(W) P(X,W)=p(X)p(W)
有:
p ( W ∣ X , Y ) p ( X , Y ) = p ( Y ∣ X , W ) p ( X , W ) ⇒ p ( W ∣ X , Y ) p ( Y ∣ X ) p ( X ) = p ( Y ∣ X , W ) p ( X ) p ( W ) ⇒ p ( W ∣ X , Y ) p ( Y ∣ X ) = p ( Y ∣ X , W ) p ( W ) ⇒ p ( W ∣ X , Y ) = p ( Y ∣ X , W ) p ( W ) p ( Y ∣ X ) \begin{align} \notag p(W \vert X,Y)p(X,Y) &= p(Y \vert X,W)p(X,W) \\ \notag \Rightarrow p(W \vert X,Y)p(Y \vert X)p(X) &= p(Y \vert X,W)p(X)p(W) \\ \notag \Rightarrow p(W \vert X,Y)p(Y \vert X) &= p(Y \vert X,W)p(W) \\ \notag \Rightarrow p(W \vert X,Y) &= \dfrac{p(Y \vert X,W)p(W)}{p(Y|X)} \end{align} p(W∣X,Y)p(X,Y)⇒p(W∣X,Y)p(Y∣X)p(X)⇒p(W∣X,Y)p(Y∣X)⇒p(W∣X,Y)=p(Y∣X,W)p(X,W)=p(Y∣X,W)p(X)p(W)=p(Y∣X,W)p(W)=p(Y∣X)p(Y∣X,W)p(W)
似然的理解,其实就是,联合概率 = 似然 * 先验,不用纠结在公式的哪里,因为我们可以写 联合概率 = 似然1 * 先验1 = 似然2 * 先验2,所以我们根据需要的物理意义称其中一个似然为后验的时候,另外一个就叫似然就行了,就是这样
1/n 形式的贝叶斯公式
一开始我看不懂这个公式是怎么来的
p ( θ ∣ D ) = p ( D y ∣ D x , θ ) p ( θ ) ∫ θ p ( D y ∣ D x , θ ′ ) p ( θ ′ ) d θ ′ p(\theta \vert D) = \dfrac{p(D_y \vert D_x, \theta)p(\theta)}{\int_{\theta} p(D_y \vert D_x, \theta')p(\theta')\mathrm{d}\theta'} p(θ∣D)=∫θp(Dy∣Dx,θ′)p(θ′)dθ′p(Dy∣Dx,θ)p(θ)
看了这个才理解 https://www.zhihu.com/question/21134457/answer/169523403
”1/n 形式的贝叶斯公式“这个名称是我瞎起的……主要是我感觉,它的物理意义就是跟 1/n 很像
就是, p ( θ ∣ D ) p(\theta \vert D) p(θ∣D) 中的 θ \theta θ 只是一个分布,但是 θ \theta θ 可以有很多种可能,就是说他是一个自变量,然后现在如果我们给定一个 θ \theta θ,那么想要知道单独这一个 θ \theta θ 在所有可能的 θ \theta θ 中的概率,所以我们分母就是已知发生 θ ′ \theta' θ′ 然后同时也发生 D D D 的所有可能的 θ ′ \theta' θ′ 的情况的概率之和,然后分子就是单独 θ \theta θ 那一种情况的概率
全概率公式
全概率公式的积分形式
离散形式的全概率公式:
p ( A ) = ∑ i p ( A ∣ B i ) p ( B i ) p(A) = \sum_i{p(A \vert B_i)p(B_i)} p(A)=i∑p(A∣Bi)p(Bi)
积分形式:
p ( A ) = ∫ p ( A ∣ B ) p ( B ) d B p(A) = \int p(A \vert B)p(B)\mathrm{d}B p(A)=∫p(A∣B)p(B)dB
也可以写为
p ( A ) = ∫ p ( A , B ) d B p(A) = \int p(A, B)\mathrm{d}B p(A)=∫p(A,B)dB
后验推理
后验预测分布 posterior predictive distribution
后验预测分布的公式:
p ( y ∣ x , D ) = ∫ θ p ( y ∣ x , θ ′ ) p ( θ ′ ∣ D ) d θ ′ p(y \vert x, D) = \int_{\theta} p(y \vert x, \theta')p(\theta' \vert D)\mathrm{d}\theta' p(y∣x,D)=∫θp(y∣x,θ′)p(θ′∣D)dθ′
或者这个参数 θ ′ \theta' θ′ 也有人写作 W
p ( y ∣ x , D ) = ∫ p ( y ∣ x , W ) p ( W ∣ D ) d W p(y \vert x, D) = \int p(y \vert x, W)p(W \vert D)\mathrm{d}W p(y∣x,D)=∫p(y∣x,W)p(W∣D)dW
一开始不知道这个公式怎么来的
看了 https://math.stackexchange.com/questions/1606372/how-to-derive-the-posterior-predictive-distribution 才懂
他这里写的形式又不一样,好像是把 x , D x, D x,D 写成了 D D D, y y y 写成了 D ′ D' D′
p ( D ′ ∣ D ) = ∫ θ p ( D ′ ∣ θ ′ ) p ( θ ′ ∣ D ) d θ ′ p(D' \vert D) = \int_{\theta} p(D' \vert \theta')p(\theta' \vert D)\mathrm{d}\theta' p(D′∣D)=∫θp(D′∣θ′)p(θ′∣D)dθ′
这里有点让我迷惑的是, y ∣ x , D y \vert x, D y∣x,D 这个形式到底是代表着 y ∣ ( x , D ) y \vert (x, D) y∣(x,D) 还是 ( y ∣ x ) , D (y \vert x), D (y∣x),D
按照他这么写,似乎是代表着 y ∣ ( x , D ) y \vert (x, D) y∣(x,D)
假设按照他这么写
使用全概率公式
p ( A ) = ∫ p ( A , B ) d B p(A) = \int p(A, B)\mathrm{d}B p(A)=∫p(A,B)dB
得到
p ( D ′ ∣ D ) = ∫ p ( D ′ , θ ∣ D ) d θ p(D' \vert D) = \int p(D', \theta \vert D)\mathrm{d}\theta p(D′∣D)=∫p(D′,θ∣D)dθ
p ( W ∣ D ) p(W \vert D) p(W∣D) 就是我们的神经网络,所以它的解析式很难写
所以我们需要一个变分推断
变分贝叶斯推理中为什么要最大化证据下界
通过变分推断,我们知道 log p(x) 可以分为证据下界+KL散度
KL 散度 > 0,log p(x) 不依赖于变分参数 θ,所以 log p(x) > 证据下界,所以才叫他下界
之后的操作就是我们要最大化这个证据下界,然后我们等价于最小化旁边的那个 KL 散度
但是为什么要最大化这个证据下界呢,我看好像很多人都直接这么说了,他们也没有解释

或者说一般的解释与我想的不符……
一般的解释是,因为 log p(x) 不好计算,所以计算它的下界,最大化它的下界,就相当于最大化 log p(x) 本身
但是有一个问题是,假设 log p(x) 不变的时候,最大化证据下界才相当于最小化 KL 散度
如果 log p(x) 一直不变的话,最大化证据下界本身不会影响 log p(x) 的呀
和
https://zhuanlan.zhihu.com/p/463062561
他们都说到了 EM 算法,但是我看不懂……
之后看了
我很喜欢他把变分表示为 ”找一个 q(w|D) 去近似 p(w|D)“,我感觉这样的记法很统一,即使这种记法没有指出 q 有自己的概率分布的参数,但是在知道了不同的记法之后,再来看的话,就感觉很统一
然后其实我看了一下,他的意思其实是,最大化 ELBO 是为了最小化两个概率分布之间的概率分布,而 ELBO 本身其实没有什么意义,就是说,如果你不是为了最小化两个概率分布的话,那么你就不会知道 ELBO 本身跟我们 ”找一个 q(w|D) 去近似 p(w|D)“ 这件事有什么关系
所以我们是为了完成 ”找一个 q(w|D) 去近似 p(w|D)“ 才去找有什么方法去实现它,然后我们就看到了 ELBO,噢,它可以用
然后第二个关键的地方我觉得是,实际上我们确实没有在算 ELBO,我们实际代码中算的就是两个概率之间的 KL 散度,所以我猜,可能是别的方法要用到这个 ELBO,但是我们代码中确实没有算 ELBO……所以我一下就知道,我不用管它了……
之后再看的话……或许我觉得我的理解又错了

左边是 BBB 原论文,右边是这个回答的理解
突然觉得这个理解是能搭配上这个论文的解释的
按照回答的理解是
log p(D) = L + KL[q(w|D) || p(w|D)]
L = E_{q(w|D)}[log p(D|w)] - KL[q(w|D) || p(w)]
log p(D) 不变,最大化 L 相当于最小化 KL[q(w|D) || p(w|D)],也就是使得 q(w|D) 与 p(w|D) 相近
那么最大化 L 相当于最小化 -L
他是从 log p(D) 开始推的
而刚好,在换了一个记法,不是记成 q(w|D) 而是记成 q(w|θ)
之前那个公式里的 θ 表示变分参数
现在 q(θ) 写为 q(w|θ),w 表示模型参数,θ 表示变分参数,那么这个概率 q(w|θ)表示,给定变分参数,获得神经网络模型参数的概率
而 p(θ|x) 写为 p(w|D),D 表示数据集,那么这个概率 p(w|D) 表示,给定数据集,获得神经网络模型参数的概率
这是我猜的,不对的话也没关系
然后这个论文中的公式推导是怎么回事呢?他是用了一个贝叶斯公式,把 p(w|D) 换了

w 是模型参数,D 是数据集,θ 是 (μ,σ),是模型参数的概率分布的参数,他现在应该是要用 θ 来近似 w,所以他这里写的是用 w|θ 来近似 w|D,w|D 我觉得应该是指的用数据集训练出来的真实的 w,w|θ 我觉得是,我们实际上不知道 w,所以我们就用 θ 表示的概率分布在计算机上代表 w
现在就是,我觉得可能是,D 数据集不依赖于模型参数 w……?因为我是从现实世界中获得数据,然后这个模型参数 w 并不是我获得 D 的原因,所以 D 不依赖于 w,但是模型参数 w 是根据 D 训练出来的,所以依赖于 D?
所以他这里才直接让 E_w(p(D)) = p(D) 了
这样的话,我觉得这两个推导里面的 q(w|D) 和 q(w|θ) 似乎是等价的
毕竟,回答中的
log p(D) = E_{q(w|D)}[log p(D|w)] - KL[q(w|D) || p(w)] + KL[q(w|D) || p(w|D)]
L = E_{q(w|D)}[log p(D|w)] - KL[q(w|D) || p(w)]
论文中的
KL[q(w|θ) || p(w|D)] = KL[q(w|θ) || p(w)] - E_{q(w|θ)}[log p(D|w)] + log p(D)
=> log p(D) = E_{q(w|θ)}[log p(D|w)] - KL[q(w|θ) || p(w)] + KL[q(w|θ) || p(w|D)]
把 θ 换成 D 就是回答中的答案
只是推导的形式不一样
概率的不同记法
我觉得这些概率的写法一直比较混乱的……
比如其实当你在做变分推断的时候,你可以不说:”找一个 q(w|θ) 去近似 p(w|D)“,其实你也可以说 ”找一个 q(w|D) 去近似 p(w|D)“
个人理解:
”找一个 q(w|θ) 去近似 p(w|D)“ 表明,你新找的这个概率有自己的一个概率分布的参数
”找一个 q(w|D) 去近似 p(w|D)“表明,你新找的这个概率和未知的这个真实概率都是从数据集中得出的
平均场 VI
在看别人的讲座 https://www.youtube.com/watch?v=xH1mBw3tb_c&list=PLe5rNUydzV9QHe8VDStpU0o8Yp63OecdW&index=4
他有一个推导我一时间没看懂

我一开始还以为是

于是我写成

后来看到别人的推导,才觉得这个变换这里应该是先写一下积分的形式才比较好懂
https://bjlkeng.io/posts/variational-bayes-and-the-mean-field-approximation/
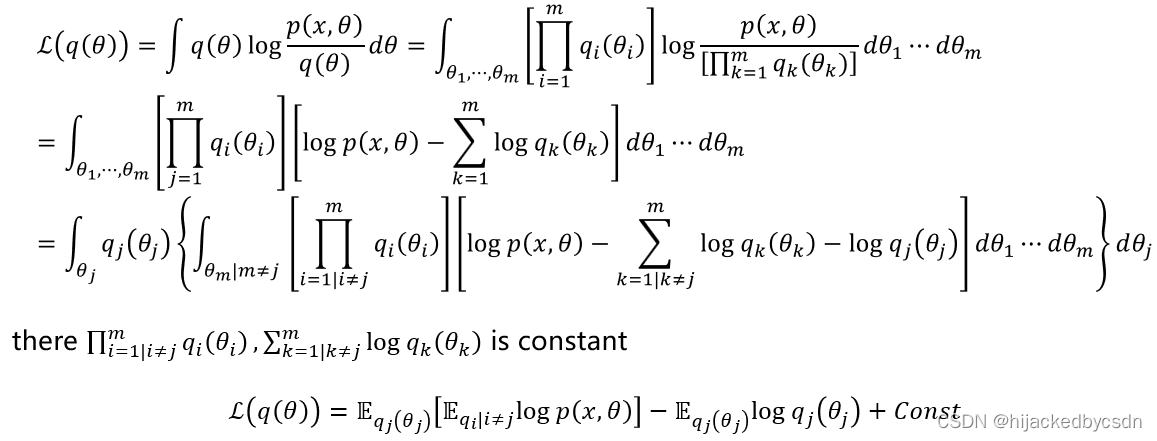

Bayes by Backprop 代码
重新参数化
一开始我看的是这个 https://www.zhihu.com/tardis/zm/art/263053978?source_id=1003
他算的损失是
loss = log_post - log_prior - log_like
对应
L = ∑ i l o g q ( w i ∣ θ i ) − ∑ i l o g P ( w i ) − ∑ i l o g p ( y i ∣ w i , x i ) \mathcal L = \sum_i \mathrm{log} q(w_i \vert \theta_i) - \sum_i \mathrm{log} P(w_i) - \sum_i \mathrm{log}p(y_i \vert w_i,x_i) L=i∑logq(wi∣θi)−i∑logP(wi)−i∑logp(yi∣wi,xi)
其中前两个的计算的方式看了一会还是可以理解的
对于 log_prior
# sample weights
w_epsilon = Normal(0, 1).sample(self.w_mu.shape)
self.w = self.w_mu + torch.log(1+torch.exp(self.w_rho)) * w_epsilon
# sample bias
b_epsilon = Normal(0, 1).sample(self.b_mu.shape)
self.b = self.b_mu + torch.log(1+torch.exp(self.b_rho)) * b_epsilon
# record log prior by evaluating log pdf of prior at sampled weight and bias
w_log_prior = self.prior.log_prob(self.w)
b_log_prior = self.prior.log_prob(self.b)
self.log_prior = torch.sum(w_log_prior) + torch.sum(b_log_prior)
对应到公式中 w w w 为模型参数, θ = ( μ , ρ ) \theta = (\mu, \rho) θ=(μ,ρ) 的话,首先要知道,这里的模型是啥,这里的模型是一个普通的线性层,他这里甚至都没写激活函数,就是一个线性层,线性层的参数是 w 和 b,也就是缩放和偏置,那么其实公式中的模型参数 w w w 对应到代码中就是 w 和 b,那么其实我要算 p ( w ) p(w) p(w) 的话,我其实就是要算出来代码中对应到公式中的 w w w 的值,然后再放到 prior 分布中计算对应的函数值
他这个文章没有说的是,他应该是假设了 p(w) 的分布是正态分布
然后他说明了,假设 q(w|θ) 是 θ 决定的 w 的正态分布
那么这个后验 log_post 的计算也很合理
self.w_post = Normal(self.w_mu.data, torch.log(1+torch.exp(self.w_rho)))
self.b_post = Normal(self.b_mu.data, torch.log(1+torch.exp(self.b_rho)))
self.log_post = self.w_post.log_prob(self.w).sum() + self.b_post.log_prob(self.b).sum()
最后他那个似然 log_like 的计算我有点不懂
def sample_elbo(self, input, target, samples):
# we calculate the negative elbo, which will be our loss function
#initialize tensors
outputs = torch.zeros(samples, target.shape[0])
log_priors = torch.zeros(samples)
log_posts = torch.zeros(samples)
log_likes = torch.zeros(samples)
# make predictions and calculate prior, posterior, and likelihood for a given number of samples
for i in range(samples):
outputs[i] = self(input).reshape(-1) # make predictions
log_priors[i] = self.log_prior() # get log prior
log_posts[i] = self.log_post() # get log variational posterior
log_likes[i] = Normal(outputs[i], self.noise_tol).log_prob(target.reshape(-1)).sum() # calculate the log likelihood
# calculate monte carlo estimate of prior posterior and likelihood
log_prior = log_priors.mean()
log_post = log_posts.mean()
log_like = log_likes.mean()
主要我是不知道为什么这个分布是均值是 y_pred 的正态分布
之后看到 https://krasserm.github.io/2019/03/14/bayesian-neural-networks/,发现这只是别人的假设而已
为什么要这么重参数化
我主要是不知道,w 变成 w = mu + sigma * epsilon 之后,我们已经知道了梯度 偏w/偏mu 和 偏w/偏sigma 了,为什么还要把 sigma 再拆开
之后发现了,其实全文我们都在说模型参数模型参数,但是我们具体也没有说模型是什么样的
然后我们一直在说,我们人为设定模型参数满足一个先验,但是不同的层具有不同的可训练参数,这些可训练参数之间是什么关系?
我也不知道是什么关系……不过我们应该默认神经网络的参数之间是独立的
他这个是假设神经网络的每一个参数都是满足一个高斯分布,然后重参数化就是把这个高斯分布的偏置和缩放做成一个变量,他是神经网络可以训练的
高斯分布的缩放必须是大于 0 的,所以他才先 exp 再 + 1 再 log,这样就能保证最终的结果是大于 0 的。先 exp 是大于 0,然后 + 1 就是大于 1,再 log 就是大于 0

实际中,我做出来的是,最内层的 rho 有可能负无限小,导致 exp(rho) 为 0,这样最终算出来 log 1 = 0
所以我才加一个 1e-8
但是实际上这个 rho 是神经网络训练的结果,如果你都能训练到负无限小了,说明你神经网络肯定哪里写错了,我这里就是写错了,忘记把反向传播的训练误差设置为负 elbo 了
别人的代码
我看了 https://github.com/Harry24k/bayesian-neural-network-pytorch/tree/master
感觉别人写的还跟一般的有点不一样
linear 层的重参数化方法不一样
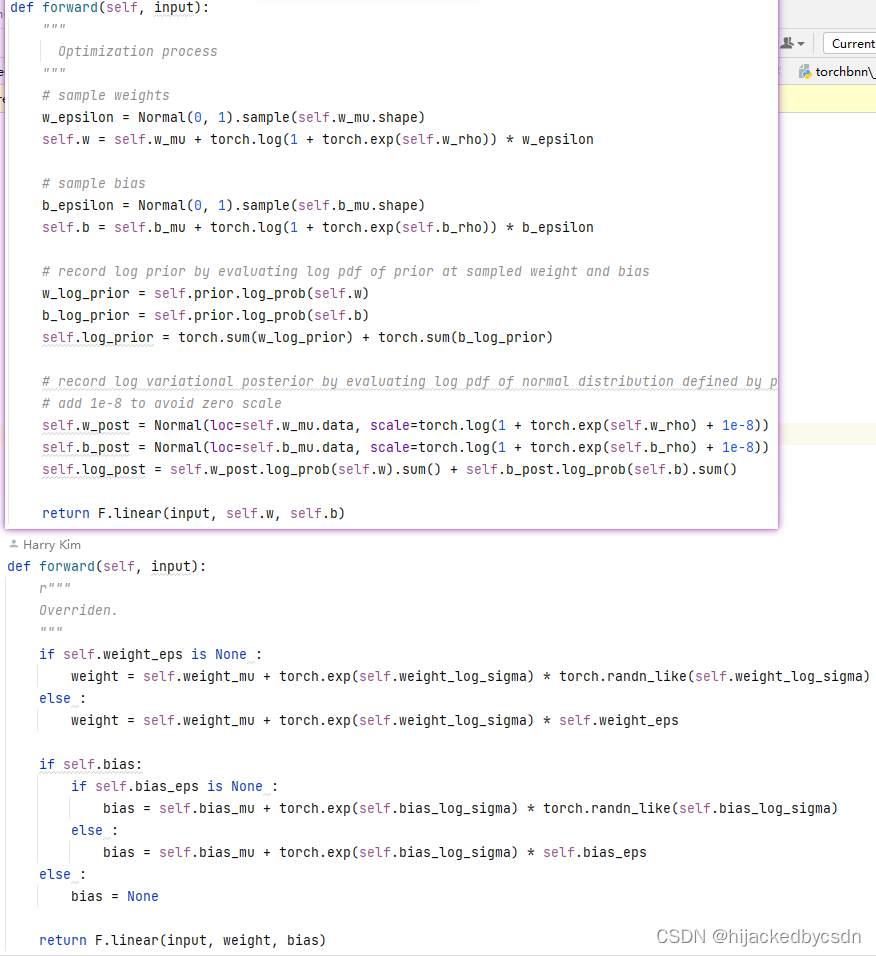
上面的我看的第一个的,知乎的代码的写法
第二个是这个 git 上的人的写法
他这里为了保证高斯分布的缩放是正的,他在最外层用的是 exp,而不是 log
这样的话,它实际上只需要一层,就是 exp(变量),而不是两层的 log(1+exp(变量))
我感觉他这样写的还挺好的
但是为了保证是完全复现 BBB 论文的话,其实两层也能 work,那为了保证跟论文一样,不改也行
计算 loss 的方法不一样
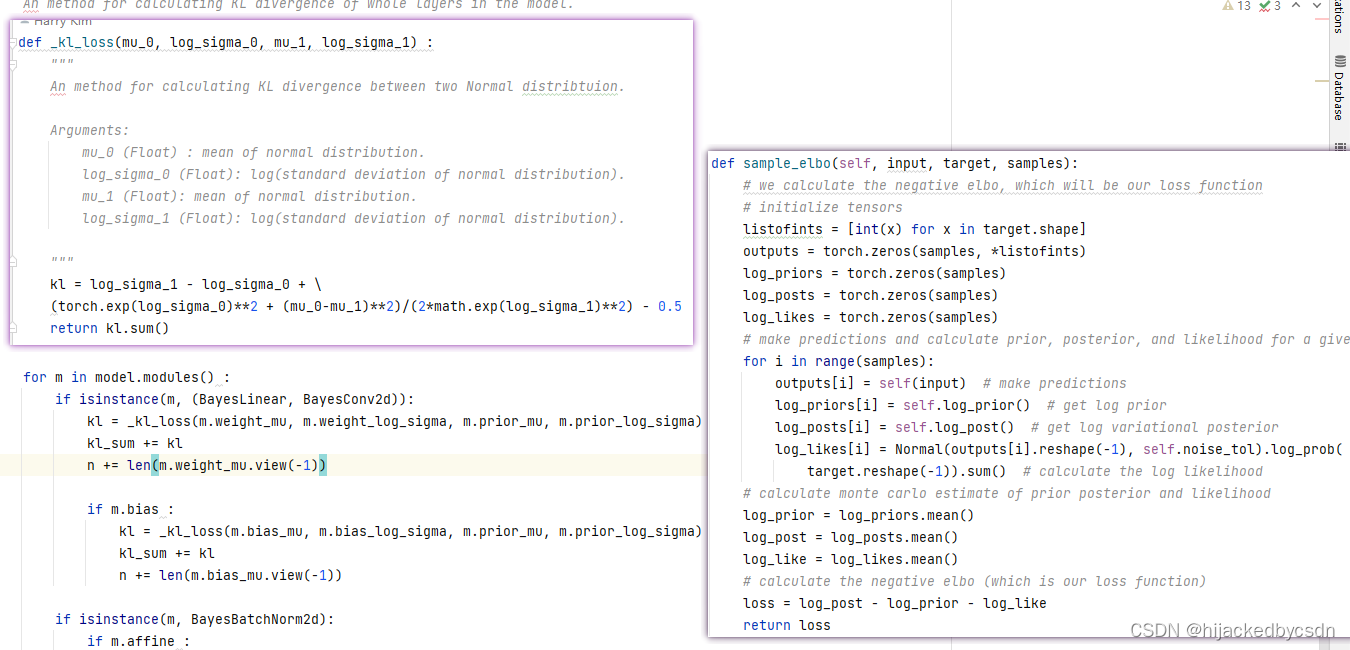
左边是它计算 loss 的方法,右边是我看的第一个知乎的方法
知乎的是把 KL loss 拆开来看,于是有一个似然概率需要用到模型预测值和真实值
而他这个是单纯的两个正态分布之间的 KL loss,这个似乎没有涉及到模型预测值和真实值之间的关系
根据 BBB 原论文,log p(D) = E_{q(w|θ)}[log p(D|w)] - KL[q(w|θ) || p(w)] + KL[q(w|θ) || p(w|D)]
BBB 原论文是最小化 KL[q(w|θ) || p(w)] - E_{q(w|θ)}[log p(D|w)] 来使得 KL[q(w|θ) || p(w|D)] 最小,也就代表近似的概率靠近真实概率
他这里好像是就是直接算两个真实的概率之间的 KL 散度,还是用解析的公式算,而不是用蒙特卡罗积分的方式来算
























 2026
2026

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








