数据结构（7）—— 排序总结_设待排文件fi={1, 4, 10, 11, 8, 0, 20, 12, 9, 5, 14, 7, -优快云博客

本文深入讲解了各种排序算法，包括插入排序、交换排序、选择排序、归并排序和基数排序等，探讨了它们的基本思想、时间与空间复杂度以及稳定性，并对比了内部排序算法的性能。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

『知识框架』

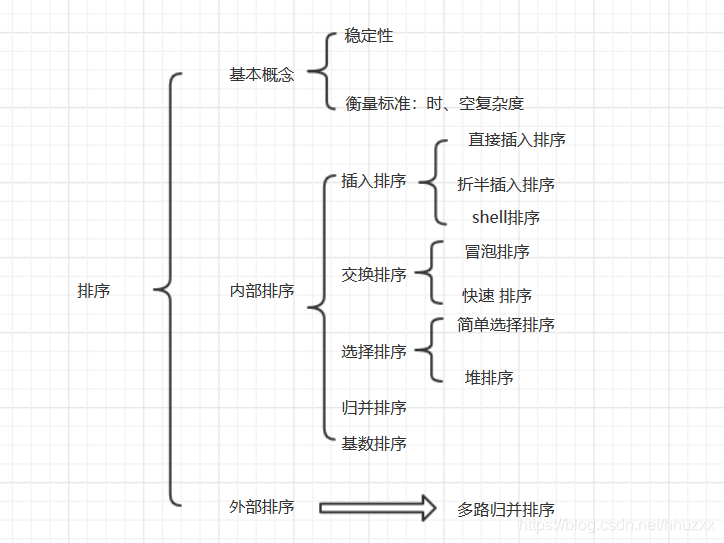
「排序基本概念」

算法的稳定性：若待排序中有两个元素 $R_{i}$ 和 $R_{j}$ ，对应关键字 $key_{i}$ 和 $key_{j}$ ，且排序前 $R_{i}$ 在 $R_{j}$ 前面，使用某一算法之后， $R_{i}$ 仍在 $R_{j}$ 之前，则称排序算法稳定。稳定性不能衡量一个算法的优劣。

排序算法分类：

内部排序：排序期间元素全部存在内存中的排序
外部排序：元素无法全部放在内存中，要在内、外存之间移动的排序

并非所有排序基于比较操作，比如基数排序

「插入排序」

基本思想：将一个待排序的记录按关键字大小插入到已经排好序的子序列中，直到全部记录插入完成

「直接插入排序」

查L(i)在L[1...i-1]中的插入位置k
将L[k...i-1]中所有元素全部后移一个位置
将L(i) 复制到 L(k)

上述过程执行n-1次得到一个有序表，空间复杂度O(1)，最好情况表元素已有序，只比较一次不移动，时间复杂度O(n)；最坏情况逆序，总比较次数 n(n-1)/2，移动次数也达到了最大，复杂度O(n^2)

直接插入排序稳定，适合顺序存储和链式村粗，大部分排序算法适合顺序存储的线性表。

「折半插入排序」

在查找插入位置时使用折半查找来实现。折半插入减少了比较次数，约为O( $n\log _{2}n$ )，比较次数与待排表的初始状态无关，仅取决于元素个数n；元素移动次数不改变。因此，折半插入复杂度O(n^2)。是一种稳定排序方法

「希尔排序」

将排序表分成L[i,i+d,i+2d....i+kd]的特殊字表，分别进行直接插入排序，当整个表已经基本有序时，再对全体进行一次直接插入排序。取一个d，分成d组，距离为d的倍数的记录放在同一组。然后排序；再取d，重复，直到d=1。

时间复杂度O(1)，最坏情况O(n^2)，n在某范围O(n^1.3)

算法不稳定

「交换排序」

交换：根据系列中两个元素关键字的比较结果兑换这两个记录在序列中的位置

「冒泡排序」

思想：待排表长n，从后往前两两比较相邻元素值，若为逆序，交换，直到序列比较完，最小的元素排在第一个位置，称一趟排序。在之后的冒泡过程中，排好的元素不参与比较。最多做n-1趟冒泡。

初始有序，比较n-1次，移动0次，最好复杂度O(n）；

初始逆序，n-1趟排序，第i趟进行n-i次比较，比较次数 n(n-1)/2，移动次数3n(n-1)/2，所以最坏O(n^2)，平均也O(n^2)

算法稳定，冒泡排序中所产生的有序子序列一定全局有序，每趟排序都会将一个元素放到最终的位置上。

「快速排序」

思想：基于分治，在待排表中选一个作为基准，通过一趟把表划分成两部分，前半部分小于基准，后半部分大于等于基准值，称一趟快排。而后递归重复上述过程，直至每个部分只有一个元素或空为止。

快排性能取决于划分操作的好坏。

空间效率：快排是递归的，最好情况 $\left \lceil \log _{2}(n+1) \right \rceil$ ，最坏O(n)，平均O( $\log _{2}n$ )

时间效率：最坏O(n^2)，一般为O( $n\log _{2}n$ )

快排是所有内部排序算法中性能最优的排序算法

快排不稳定，每趟排序都会将一个元素放到最终的位置上。

「选择排序」

「简单选择排序」

思想：假设表L[1...n]，第i趟排序从L[i...n]中选择关键字最小的元素与L(i)交换，经过n-1趟确定最终排序结果。

简单选择排序，移动操作次数很少；元素间比较的次数与序列的初始状态无关，始终 n(n-1)/2次，复杂度O(n^2)

算法不稳定，每趟排序会将一个元素放到最终的位置上

「堆排序」

思想：树形选择排序方法，视为一棵完全二叉树的顺序存储结构，利用双亲和孩子结点的关系，选择元素排序。

建堆后，n-1次向下调整，时间与树高有关，为O(h)

在元素个数为n的序列上建堆，时间复杂度O(n)

算法不稳定。

「归并排序和基数排序」

「归并排序」

归并：将两个或两个以上的有序表组合成一个新的有序表。

思想：设有两段有序表A[low,mid]、A[mid+1,high]存在同一顺序表中的相邻位置，先复制到辅助数组B中。每次从对应B中两个段取出一个记录进行关键字的比较，将较小者放入A，当数组B中有一段的下标超出其对应的表长时，将另一段剩余部分直接复制到A中。

递归形式的2路归并排序算法基于分治。

空间效率：O(n)

时间效率：每趟归并时间复杂度O(n)，共需进行 $\left \lceil \log _{2}n \right \rceil$ 趟归并，算法时间复杂度O( $n\log _{2}n$ )

算法稳定

「基数排序」

基数排序不基于比较，借助“分配”和“收集”对关键字进行排序

空间效率：一趟排序需要辅助存储空间r（r个队列），所以为O(r)

时间效率：进行d趟分配和收集，一趟分配O(n)，一趟收集O(r)，复杂度O(d(n+r))，它与序列的初始状态无关

算法稳定

「内部排序算法比较」

算法种类	时间复杂度			空间复杂度	是否稳定
算法种类	最好情况	最坏情况	平均情况	空间复杂度	是否稳定
直接插入排序	$O(n)$	$O(n^{2})$	$O(n^{2})$	$O(1)$	YES
冒泡排序	$O(n)$	$O(n^{2})$	$O(n^{2})$	$O(1)$	YES
简单选择排序	$O(n^{2})$	$O(n^{2})$	$O(n^{2})$	$O(1)$	NO
希尔排序				$O(1)$	NO
快速排序	$O(n\log_{2}n)$	$O(n\log_{2}n)$	$O(n^{2})$	$O(\log_{2}n)$	NO
堆排序	$O(n\log_{2}n)$	$O(n\log_{2}n)$	$O(n\log_{2}n)$	$O(1)$	NO
2路归并排序	$O(n\log_{2}n)$	$O(n\log_{2}n)$	$O(n\log_{2}n)$	$O(n)$	YES
基数排序	$O(d(n+r))$	$O(d(n+r))$	$O(d(n+r))$	$O(r)$	YES

「外部排序算法」

「外部排序的基本概念」

外部排序：需要将待排序记录存储在外存上，排序时再把数据一部分一部分地调用内存进行排序，排序过程中需要多次进行内存和外存之间的交换，对外存文件中的记录进行排序后的结果仍然放到原有文件中。

外部排序方法通常采用归并排序方法，包括两个独立的阶段：首先，根据内存缓冲区的大小，把外存上含n个记录的文件分成若干长度为h的子文件，依次读入内存并利用内部排序算法进行排序，将排序后的结果写回外存，称这些有序子文件为归并段；然后对这些归并段进行逐趟归并。

外部排序的总时间：内部排序的时间+外存信息读写时间+内部归并所需时间：

$t_{ES}=r\cdot t_{IS}+d\cdot t_{IO}+S\cdot (n-1)\cdot t_{mg}$

$t_{IS}$ ：对每个初始归并段内部排序的时间

$r$ ：初始归并段的个数

$d$ ：访问外存块的次数

$t_{IO}$ ：每个块的存取时间

$S$ ：归并趟数

$n$ ：每趟参加2路归并的记录个数

$t_{mg}$ ：每做一次内部归并时，取得一个关键字最小记录的时间

一般的，对r个初始归并段，做m路平衡归并，归并树可用严格的m叉树表示。归并趟数 $S$ = 树的高度 = $\left \lceil \log _{m}r \right \rceil$ 。可见，只要增大归并路数m，或减少初始归并段的个数r，都能减少归并趟数S，进而减少I/O次数d，达到提速的目的。

「多路平衡归并与败者树」

增加归并路数m时，内部归并的时间也会增加。做内部归并时，在m个元素中选关键字最小的记录需要比较m-1次。每趟归并n个元素需要（n-1）(m-1)次比较，S趟归并需要比较次数： $S(n-1)(m-1)=\left \lceil \log_{m}r \right \rceil(n-1)(m-1)=\left \lceil \log_{2}r \right \rceil(n-1)(m-1)/\left \lceil \log_{2}m\right \rceil$ ，因此不能使用普通的内部归并排序算法。

为了使内部归并不受m的增大的影响，引入败者树。败者树可视为一棵完全二叉树。每个叶节点存放各归并段在归并过程中当前参加比较的记录，内部结点记录左右子树的“失败者”，让胜者继续比较，一直到根节点。大的为败者，小的为胜者，根节点指向的树为最小数。

采用此方法，m路归并树的败者树深度 $\left \lceil \log_{2}m\right \rceil$ ，从m个记录找最小，最多需要 $\left \lceil \log_{2}m\right \rceil$ 次比较，总的比较次数为： $S(n-1)\left \lceil \log_{2}m\right \rceil=\left \lceil \log_{m}r \right \rceil(n-1)\left \lceil \log_{2}m\right \rceil=(n-1)\left \lceil \log_{2}r\right \rceil$

使用败者树后，与m无关，提高了排序速度。但并不是归并路数越大越好。归并路数m增大时，要增加缓冲区个数。

「置换-选择排序」

减少初始归并段的个数r也可以减少归并趟数S。

设初始待排文件为FI，初始归并段文件为FO，内存工作区为WA，内存工作区可容纳w个记录，置换-选择算法步骤：

（1）从待排文件FI输入w个到WA

（2）从WA中选择最小的记录，记为MINMAX

（3）将MINMAX输出到FO

（4）若FI未读完，从FI继续读入记录到WA

（5）从WA中所有比当前MINMAX大的关键字中选择比MINMAX小的记录，作为新的MINMAX

（6）重复（3）-（5），直到WA中选不出新的MINMAX为止，由此得到一个初始归并段，输出一个结束标志到FO中

（7）重复（2）-（6），直到WA为空。得到所有初始归并段

选择MINMAX记录的过程利用败者树实现

「最佳归并树」

文件经过置换-选择，得到长度不等的初始归并段。如何组织归并段的归并顺序，使得IO次数最少呢？

归并树中，各叶节点表示参加归并的一初始归并段，叶节点上权值表示归并段的记录数，根节点表示最终生成的归并段，叶节点到根节点的路径长度表示在归并过程中的归并趟数，各非叶节点代表新的归并片段，则归并树的带权路径长WPL即为归并过程中的总读记录数。为了优化WPL，可引入哈夫曼树的思想推广到m叉树。

最佳归并树：总IO次数达到最少

若初始归并段不足以构成一棵严格m叉树时，需要添加长度为0的“虚段”，如何确定虚段个数？

设度为0的结点 $n_{0}$ 个，度为m的结点 $n_{m}$ 个，对严格m叉树有 $n_{0}=(m-1)n_{m}+1$ ，由此得 $n_{m}=(n_{0}-1)/(m-1)$

若 $(n_{0}-1)\%(m-1) = 0$ ，说明正好可以构成m叉树
若 $(n_{0}-1)\%(m-1) = u\neq 0$ ，有u个结点多余，不能包含在m叉树中。为构造包含所有 $n_{0}$ 个初始归并段的m叉树，在原有 $n_{m}$ 个内结点基础上增加一个内结点。在归并树中代替一个叶节点的位置，被代替的叶节点加上多出来的u个结点，再加上m-u-1个空归并段，就可建立归并树。