一、有源滤波器和无源滤波器的区别
无源滤波器是一种由电感、电容和电阻等无源器件构成的滤波电路,又称无源 LC 滤波器。当LC 或 RC 等元件组成选频网络后,有用信号可以无衰减或轻微衰减地通过同时对干扰信号进行尽可能强的衰减。在电路中,电容的阻抗随频率的增加而减小,而电感的阻抗则随频率的增加而增加,不同频率的信号会受到不同程度的衰减或放大,从而实现对特定频率信号的滤波处理。
有源滤波器是一种利用有源元件(如运算放大器)与无源元件(如电阻、电容、电感等)结合,来实现信号处理的电路。其工作原理是通过检测补偿对象的电压和电流,经运算得出补偿电流的控制量信号,然后依据控制算法对 PWM 逆变器进行控制,进而得到补偿电流,该补偿电流与负载电流中的谐波电流抵消,从而实现滤波功能。
| 性能 | 无源滤波 | 有源滤波 |
| 滤波效果 | 通常只能滤除特定频率信号 | 可动态滤波且效果好 |
| 频率特性 | 谐振点固定 | 不受系统频率影响 |
| 阻抗特性 | 受系统阻抗影响 | 能在不同阻抗条件下运行 |
| 负载特性 | 滤波效果随负载变化 | 不受负载变化影响 |
| 成本 | 结构简单成本低 | 电路结构复杂成本高 |
二、无源滤波器仿真
以截止频率为482KHz的RC低通滤波器为例子,其仿真电路如下图:
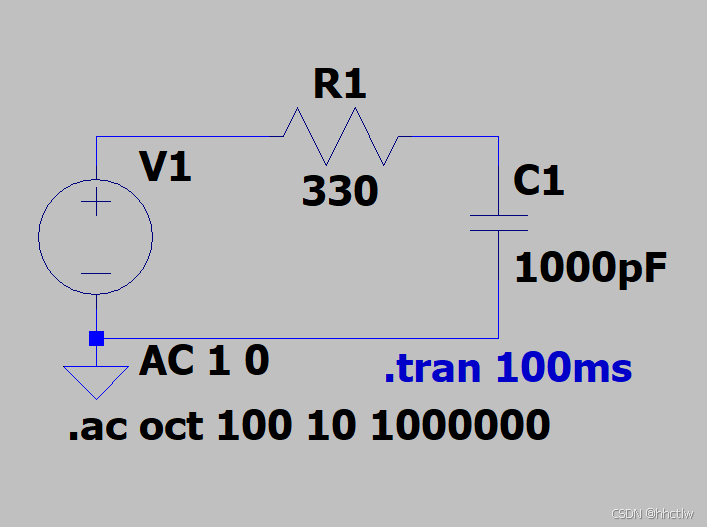
图2_1 无源RC电路图
电源选择交流电压源,其具体参数如下图:
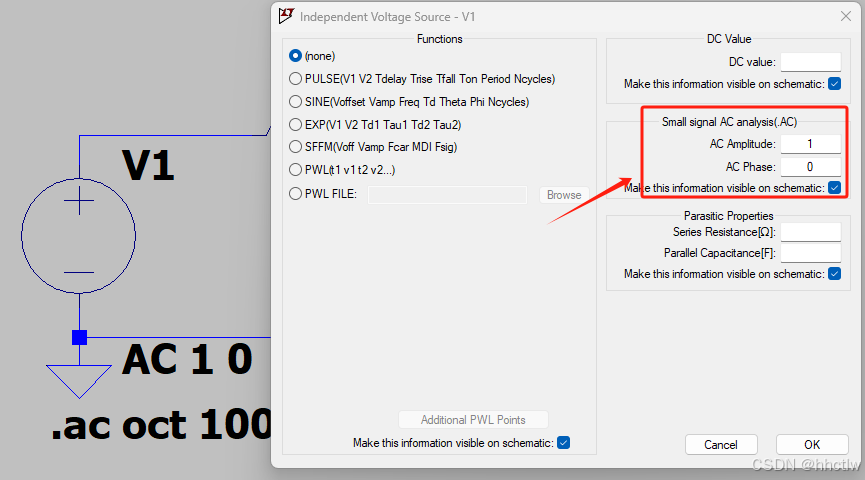
图2_2 电压源参数图
开始频率到停止频率和节点设置如下图:
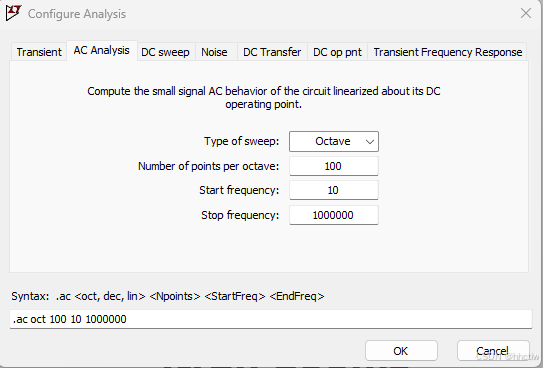
图2_3 仿真参数设置图
截止频率的衰减率是指在滤波器的截止频率附近及以外,信号幅值随频率变化而衰减的速率。在无源一阶低通滤波器情况下,当信号达到截止频率时,信号幅值衰减为输入幅值的约0.707倍,衰减量为。在截止频率之后,频率每增加10倍,信号幅值就衰减
。 通过截止频率计算公式可知
,在实际测试中发现,当电阻减小电容增加时,滤波曲线会更加趋于平缓,无法达到较为理想的滤波效果,而在电容过小的情况下,可能会使负载对滤波电路的影响增大,降低滤波电路的稳定性和可靠性,于是选择
,
作为滤波电阻和电容,其曲线图如下,
频率的信号刚好在
附近,符合理论要求。
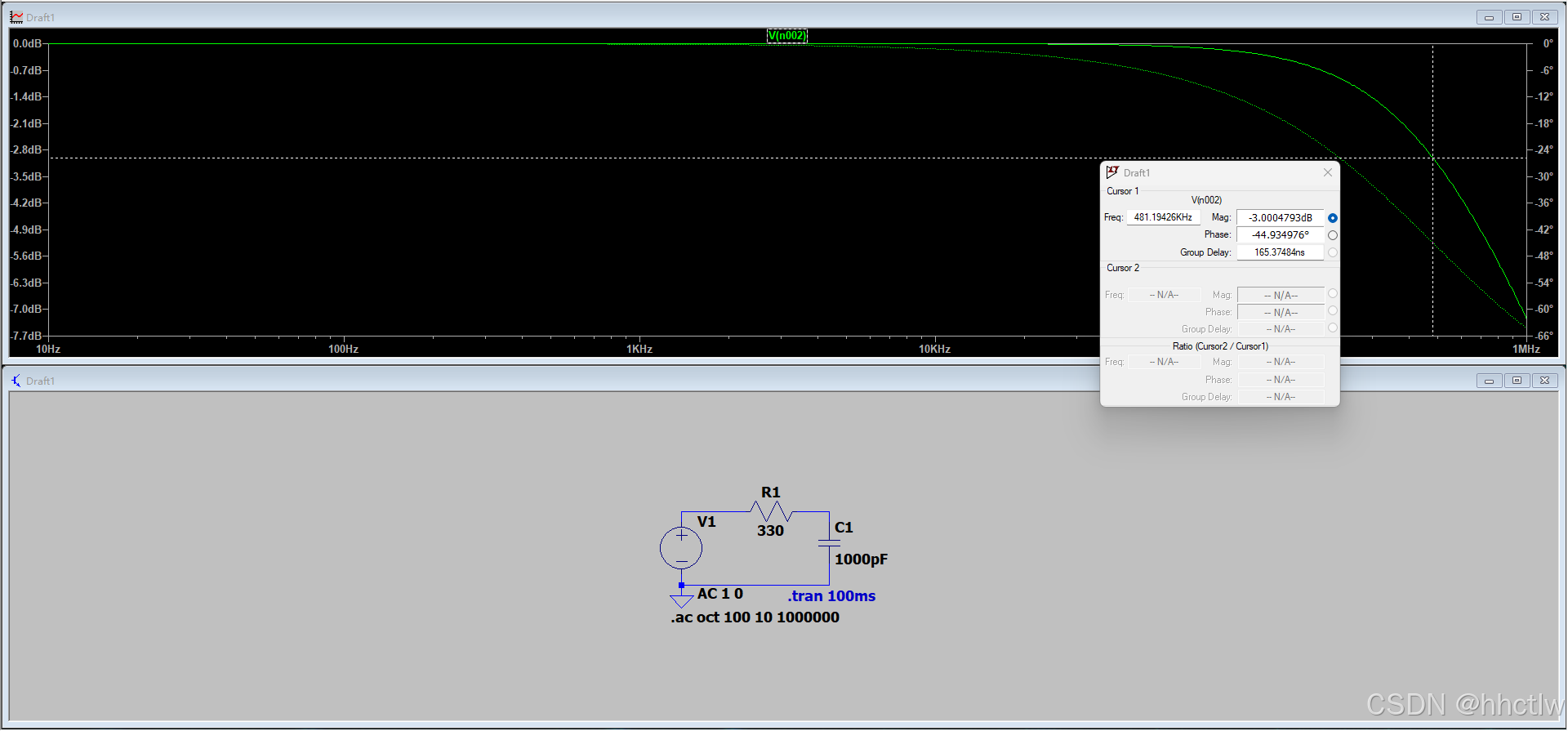
图2_4 截止频率及伯德图
三、有源滤波器仿真
1.有源滤波器设计网址
由于有源滤波器复杂的电路结构和功能各不相同,可以通过滤波器设计软件或者网站进行设计,下面是以亚诺德半导体公司开发的软件进行设计的流程。
滤波器设计向导:https://tools.analog.com/cn/filterwizard/
在选择滤波器类型(分为低通、高通、带通,这里以低通有源滤波器为例)后,进入详细规格界面,可以通过调整通带和阻带的参数来调整伯德图的曲线。
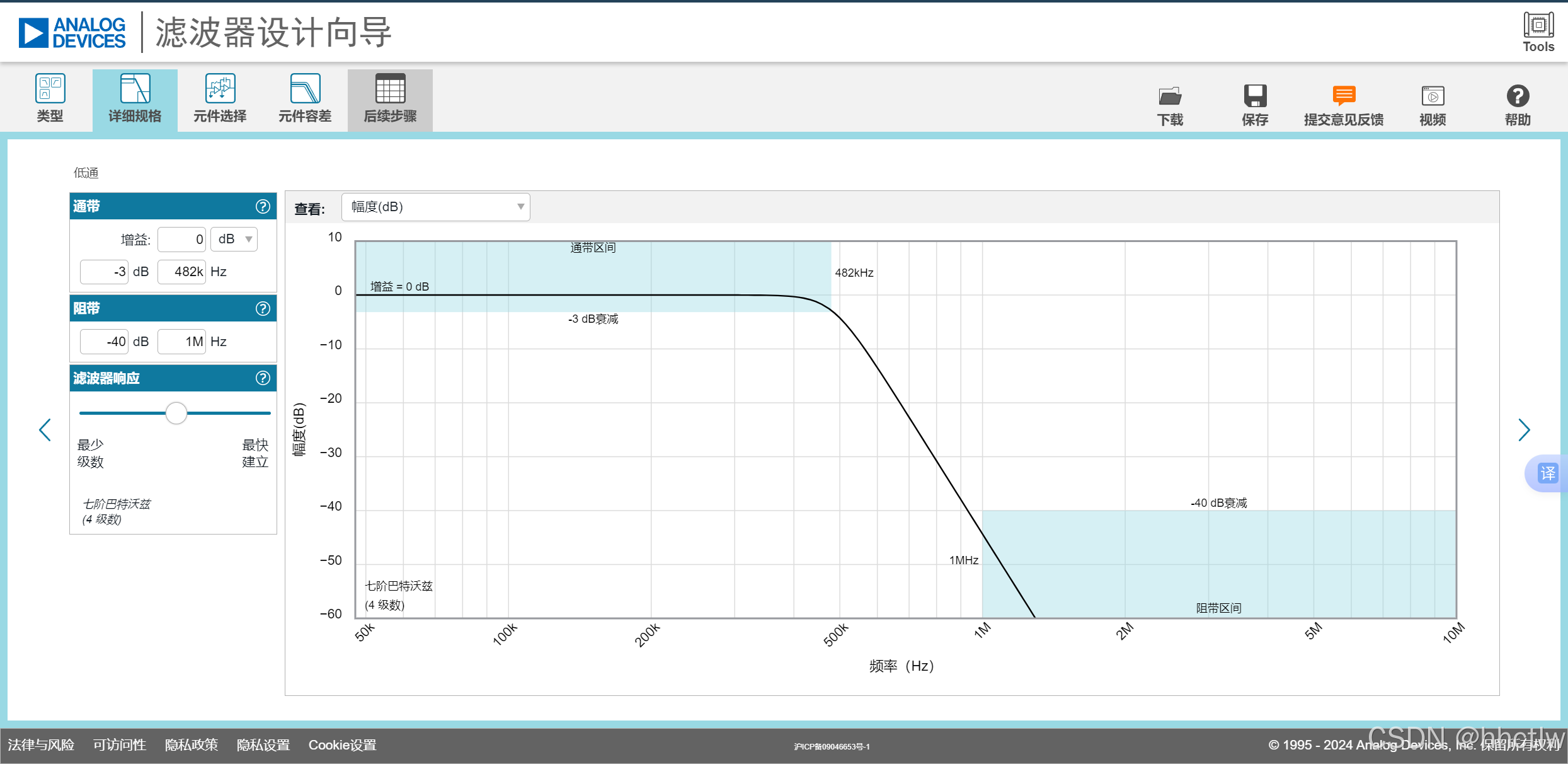
图3_1 设计伯德图
在滤波器响应栏目里,可以选择适合自己设计条件的响应,不同的响应特性会导致伯德图的结果差异。
| 滤波器响应 | 特性 |
| 切比雪夫 | 提供通带和阻带之间的最陡峭转换,因而需要最少级数 |
| 巴特沃兹 | 器件数量与其他特性之间的良好平衡,提供通带和阻带之间的最陡峭转换,同时仍然避免峰化。 |
| 巴特沃兹-贝塞尔 | 介于贝塞尔响应和巴特沃兹响应之间的过渡滤波器,性能兼具这两类响应的特点。 |
| 贝塞尔 | 提供通带和阻带之间的最平缓转换,阶跃响应良好,对元件变化的低敏感度 |
在元件选择栏可以查看网站所生成的对应滤波器电路,还可以点击“查看”切换幅度、相位、相位延迟、阶跃响应、输入阻抗、噪声、功率、电压范围、级数等特征。在元件容差栏目可以看到相关元器件所需精度,方便实际设计时候的元器件选取。最后还可以导出报告进行LTspice仿真。
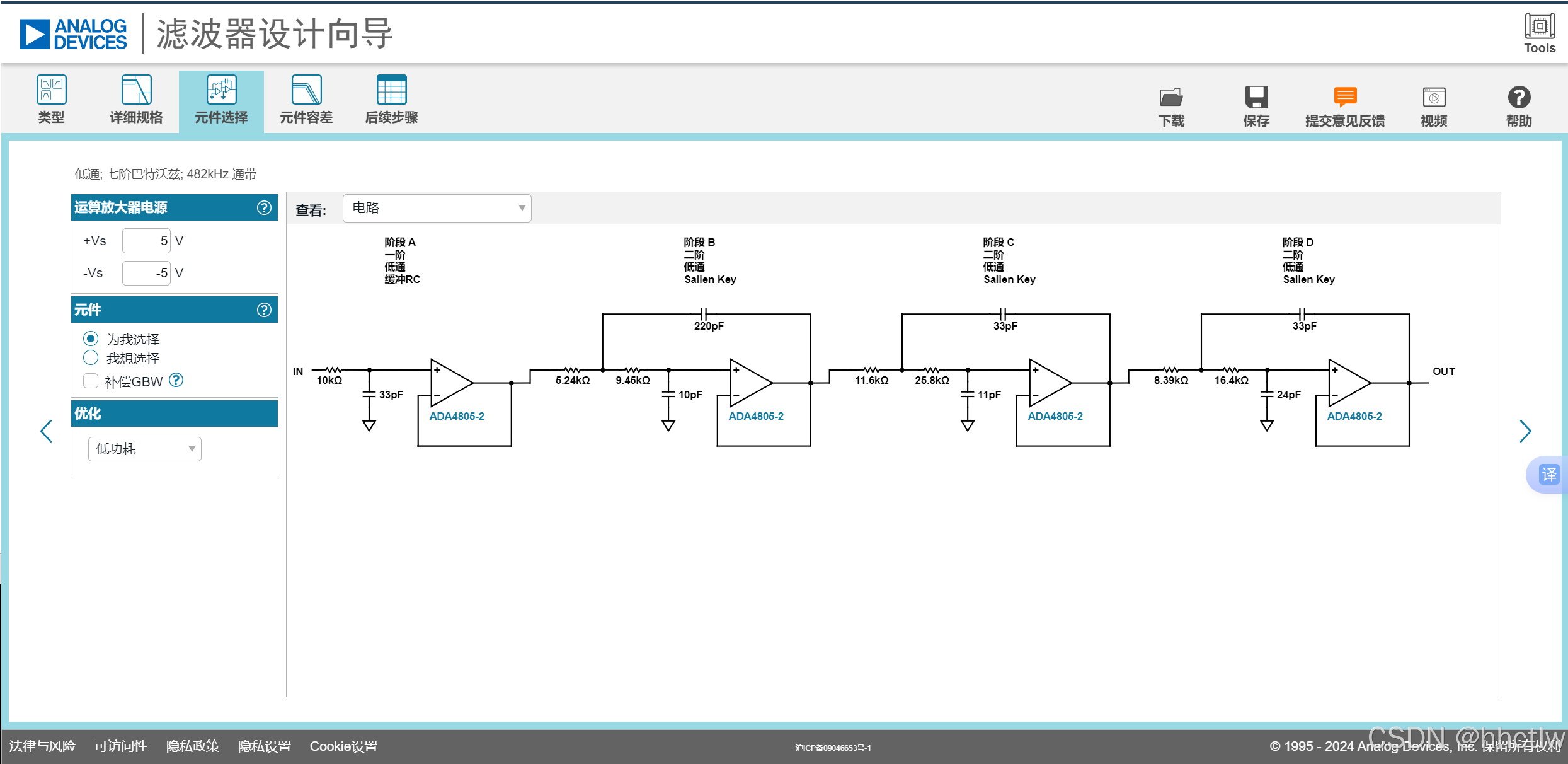
图3_2 具体电路图
2.滤波器的通带和阻带
滤波器的通带是指信号能够顺利通过滤波器而不会产生明显衰减的频率范围。在这个频率范围内,滤波器对信号的影响较小,信号的主要特征和信息能够得以保留。阻带是指滤波器能够有效阻止或大幅衰减信号的频率范围。在阻带内,信号的能量被大量抑制,从而达到滤除不需要的频率成分的目的。
通带宽度较宽时,可以允许更广泛的频率成分通过滤波器,有助于保留信号中的更多细节和信息,从而更好地保持信号的完整性。通带较窄时,滤波器对通带外频率成分的抑制能力相对较强,能够更有效地阻挡不需要的信号和噪声进入通带,提高信号的抗干扰能力。
阻带宽度较宽时,能够覆盖更广泛的不需要的频率范围,从而更有效地滤除各种干扰信号和噪声。较大的阻带可以使滤波器在频率选择性方面表现更好,能够更精确地分离出需要的信号和不需要的信号。
3.LTspice仿真
此次选用的是低通七阶巴特沃兹低通有源滤波器模型,通过下载网站上的Spice仿真模型就可以了。
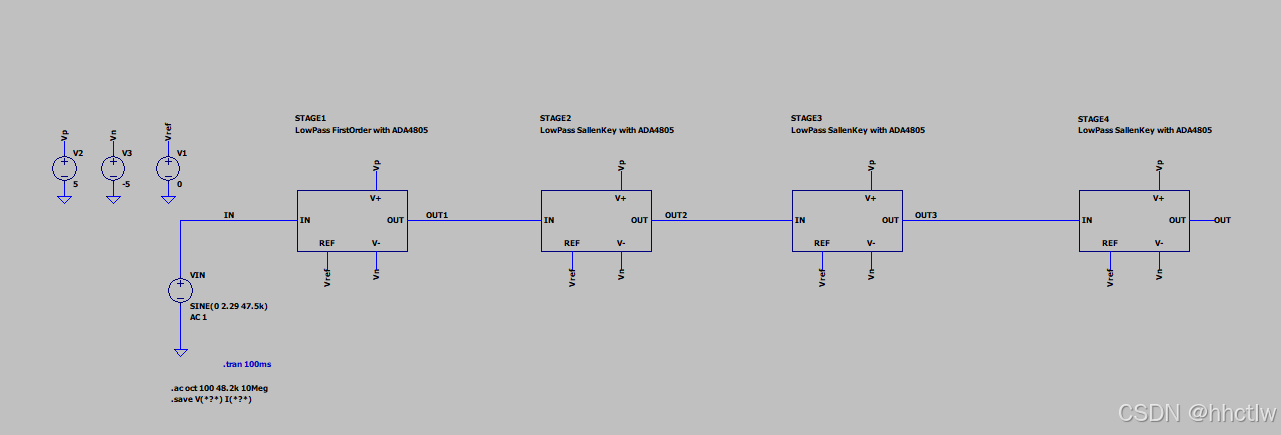
图3_3 整体电路图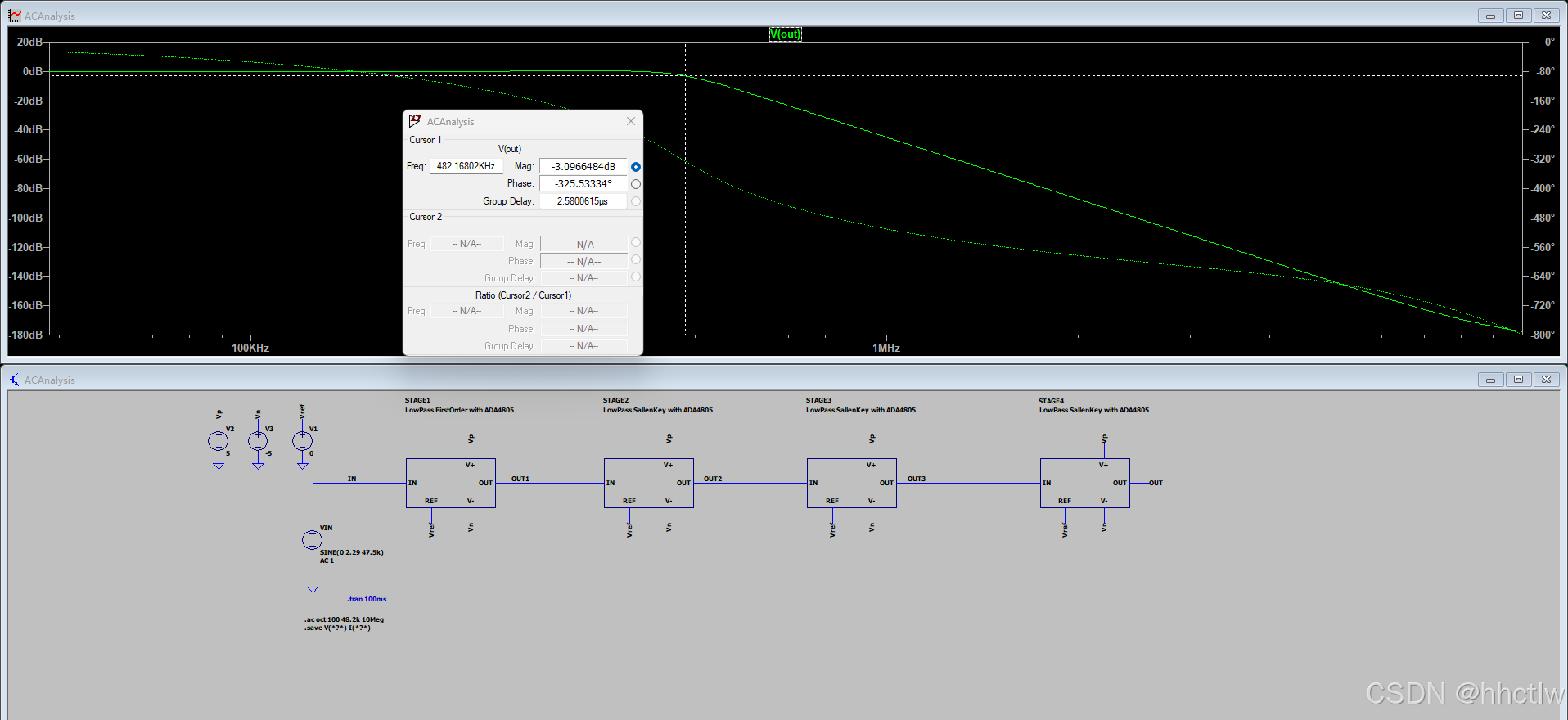
图3_4 截止频率伯德图
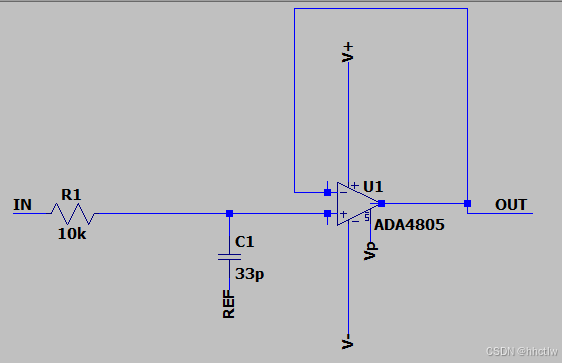
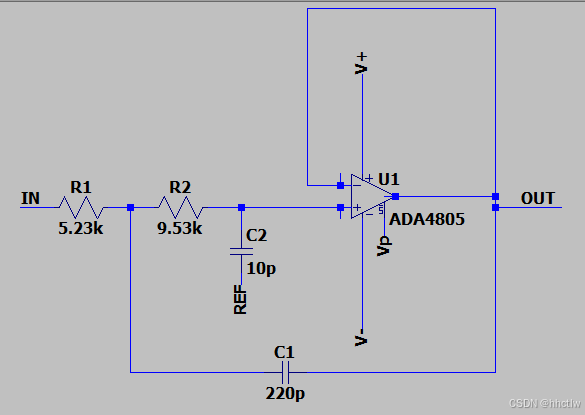
图3_5 阶段A一阶低通缓冲RC 图3_6 阶段B二阶低通Sallen Key
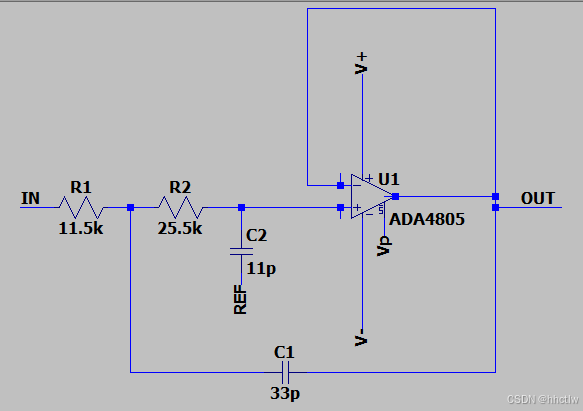
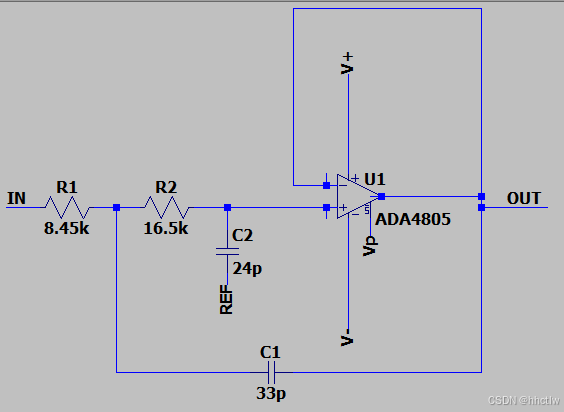
图3_7 阶段C二阶低通Sallen Key 图3_8 阶段D二阶低通Sallen Key




















 4575
4575

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








