小样本学习论文--Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks

一、前言

  学过深度学习的同学都应该知道，深度学习算法的精度是要靠数据的量来保证的，我们人类可以在看到若干次狗的样子后，就学会如果分辨狗，但是深度学习的算法可能要看上很多次。在很多领域中，数据的获取的非常昂贵的。如果让机器能够像人类一样只需要看几次就能分辩出物体是当下研究的热点。
  写这篇博客来记录一下最近看的一篇关于小样本学习的文章，文章来源Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks，作者来自伯克利大学，截至写本篇博客完稿，谷歌学术上的引用达到500+，也算是一篇小有影响力的论文。

二、论文解读

1、概述

  我们注意一下文章的title，其中有三个关键字Model-Agnostic（与模型无关的）、Fast Adaptation（快速适应）、Deep Networks（深度网络）。这三个关键字告诉我们这篇文章提出的方法，（本人感觉更像是思想或者框架）可以应用在各种神经网络的模型，并且可以快速适应不同的任务。下面我们来一起了解这三个关键字在文章中具体含义。
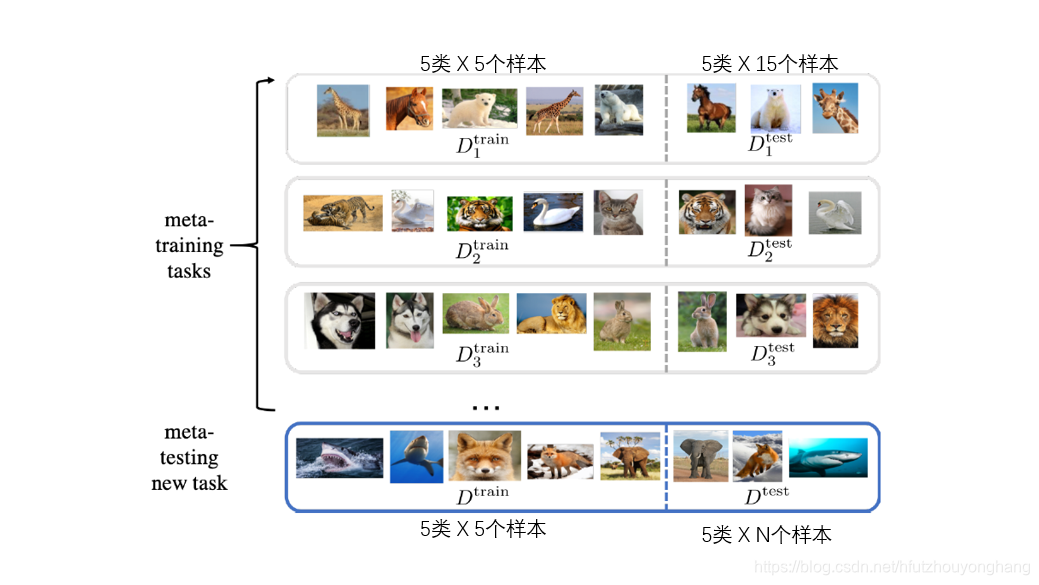
  先介绍一下一些小样本学习（Few Shot Learing）中的一个概念，这也是一开始困惑我的概念，即 N-way N-shot。N-way 的意思是N分类，N-shot是在学习的样本中，每个类只提供5个样本，比如说让你学习辨认一只猫，只有5张5的照片供你学习。这篇文章做了3个实验，分别是有监督的图片分类，一个强化学习的实验，还有一个回归的实验。这几个实验的代码放在了一起，有点复杂。在这篇博客中，只以有监督的图片分类为例来解析代码。
在5-way 5-shot的分类实验中，使用的数据集是miniImagenet，这个数据集中有100个类别的图片，每一个类别中有600张图片，大概是100类生活中常见的自然与生活中物品的集合。每张图片的大小是84x84的大小，被划分成了train(64)、test(20)、val(16)三个子集。

2 、主要内容

2.1 问题设定

  小样本元学习的目标是训练一个网络，这个网络可以经过少量的迭代次数快速的适应到新的任务中。定义一个模型 $f$,使得对于输入的X，会产生$a$. 我们训练这个网络使得它可以适应不同的无限的任务。
$$f(x)=a$$
  Task，在图片分类的这个实验中，可以被定义为下式，其中$L()$是损失函数，这个损失是指在测试集上的损失，会在下面详细叙述。$q()$是样本的分布。
T = { L ( x 1 , a 1 ) , q ( x 1 ) } T =\{ { L(x_1,a_1),q(x_1) }\} T={ L(x1​,a1​),q(x1​)}
  在这个模型中，作者考虑了一个Tas的分布$p(T)$,在k-shot的情境下，使用k个样本训练模型，让模型学习从$p(T)$中抽取的新$t_i$，这k个样本是从$q_i$中抽取的，然后产生$t_i$的$L_{t_i}$。在meta-learning的过程中，使用$q_i$中没有用过的新样本来测试。模型f通过在$q_i$新样本上的 $testerror$的变化来提升的。也就是说在在每个任务中测试样本上的error作为了meta-learning过程的train error。

2.2 与模型无关的元学习算法

  其实这个算法看起来很复杂，但是理解了之后，也没有很多奇怪的地方。首先我们来看一下上面所说的Task是什么。
所谓的task在图片分类的这个实验中就是一个普通的卷积神经网络，当然作者实验中也提供了不是卷积神经网络的普通网络的版本。这个网络图入下：

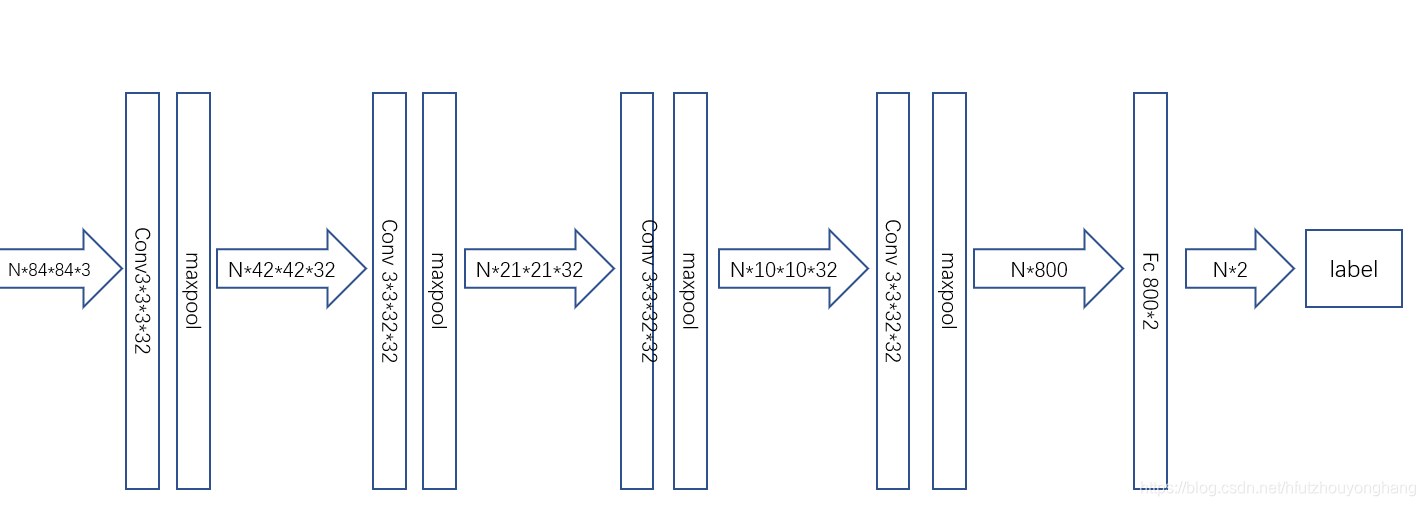
  当然这个卷积神经网络在具体使用的时候，是有点策略上的不同的。我们来看一下模型的算法流程：

  其中 $p(T)$ 是Task的分布，其实在实现中并没有去特别的设定，个人觉得就是对样本采样的那一块就顺带形成了，只是不清楚是什么分布。 $\alpha ,\beta$分别是task中的进行梯度下降的学习率、和meta-learning过程的学习率， $\theta$ 是模型(神经网络的参数) $f$的权重参数。

1. 初始化参数，这个没什么好说的
2. while：
3. 抽取Task，就是形成可能由不同内别图片组成的数据集，在作者提供的代码中，设定一个抽取4个Task，作为meta-learning的一个batch。在5-way 5-shot的情境下，作者为一个task抽取了100张照片，也就是5x20，5个类别，每个类别20张图片。task之间的5个类别有可能由重复的类别，也有可能不一样，这个是随机的。
4. 对于每个Task：
5. ，采样数据，把数据分成两部分，在5-way 5-shot设定中，一个类别只能使用5个类别来学习，那么把这100张照片分成5x5的训练集，以及5x15的验证集.
6. 计算使用训练集得到的Loss，在图片分类的实验中，使用的是交叉熵函数。
7. 通过Loss来计算SGD
8. 使用验证集在经过6，7步调整的权重下计算test error。6，7，8三个步骤在图片分类的实验中循环了5次。
10. 使用4个Task中的test error（5次循环中的最后一次）的平均值作为meta-learning的损失函数，来进行SGD过程。
11. end

  通过一个图例来辅助讲解一下：

  在一个task中，使用左边的训练集做5次SGD的过程，再使用右边的测试集计算test error，在meta-learning过程中，把一个batch的4个task的test error平均一下作为loss再去进行优化。这个过程结束后，神经网络的权重到达了下图中的P点

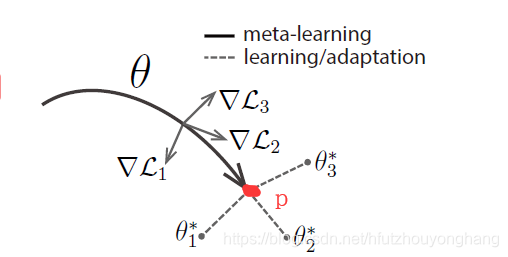
  那么，我们再使用这个模型或者测试这个模型的准确度怎么用呢？在博客的最前面，我们说把100类图片分成了3个子集，train中有64个类，用于上述的meta-learning。现在要将这个模型用在新的任务集具有16个类的test数据集上。仔细一想，训练好的模型并没有看见过test数据集中任何类啊。现在就是要说title中的Fast Adaptation的关键字了，在5-way 5-shot设定中，在测试的时候从test数据集中随机抽取5个类，每个类抽取N(>5)张照片，其中每个类抽取5张照片，用来微调模型中的参数，比如说在一个新任务下，把模型的参数调整至 θ 3 ∗ \theta_{3}^* θ