威尔逊定理

最新推荐文章于 2021-07-16 19:28:54 发布

原创最新推荐文章于 2021-07-16 19:28:54 发布 · 460 阅读

0 ·

CC 4.0 BY-SA版权

本文介绍了一种利用威尔逊定理判断特定形式数是否为质数的方法，并通过编程实现了一个序列的生成，该序列用于记录小于某个界限内满足特定条件的质数个数。文章展示了完整的C++代码实现。

威尔逊定理

当p为质数时 (p-1)! ≡ -1(mod p)

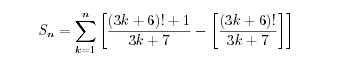
在这里插入图片描述
此题输入一个数n求解Sn，就是运用了威尔逊定理
其中[x]的含义是取不大于x的最小整数
那么当3k+7为质数时，发现那一筐值为1；当3k+7不为质数时，那一筐值为0

代码如下

#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
const int maxn=1e6+1;
int s[maxn];
int sushu(int n)
{
	if(n==1) return 0;
	for(int i=2;i<=sqrt(n);i++)
	{
		if(n%i==0)
		return 0;
	}
	return 1;
}
void init()
{
	s[0]=0;
	for(int i=1;i<maxn;i++)
	{
		if(sushu(3*i+7)==1)
		s[i]=s[i-1]+1;
		else
		s[i]=s[i-1];
	}
}
int main()
{
    init();
    int t,n;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d",&n);
        printf("%d\n",s[n]);
    }
    return 0;
}