二叉树的链式存储

顺序存储

有n个节点的完全二叉树可以用有n+1个元素的数组进行顺序存储，节点号和数组下标 一一对应。
不完全二叉树通过添加虚节点构成 完全二叉树，然后用数组存储，这要浪费一些存储空间。

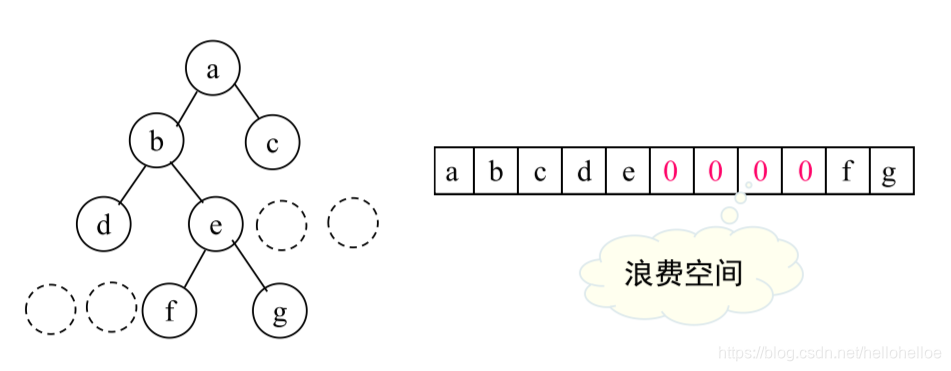
最坏的情况下，一个深度为k且只有k个结点的单支树却需要长度为2^k-1的一维数组。
总结： 顺序存储浪费空间。

链式存储

数据的描述

描述： 数据域+左右指针域

typedef char datatype;

typedef struct node {
	datatype data;
	struct node *lchild;//左孩子
	struct node *rchild;//右孩子
}btree, *btree_t;

二叉树的创建

树的结构定义是一个递归的定义，即在树的定义中又用到了树的概念。所以创建也采用递归的方式创建。

btree_t createBtree()
{
	//1.获取数据
	datatype x;
	btree_t T = NULL;

	scanf("%c", &x);

	//2.数据有效，创建根结点存放
	if('#' == x)
		return NULL;

	T = (btree_t)malloc(sizeof(btree));
	if(NULL == T)
	{
		perror("malloc");
		return NULL;
	}

	T->data = x;

	//3.还有数据，递归创建左结点存放
	T->lchild = createBtree();

	//4.还有数据，递归创建右结点存放
	T->rchild = createBtree();

	return T;
}

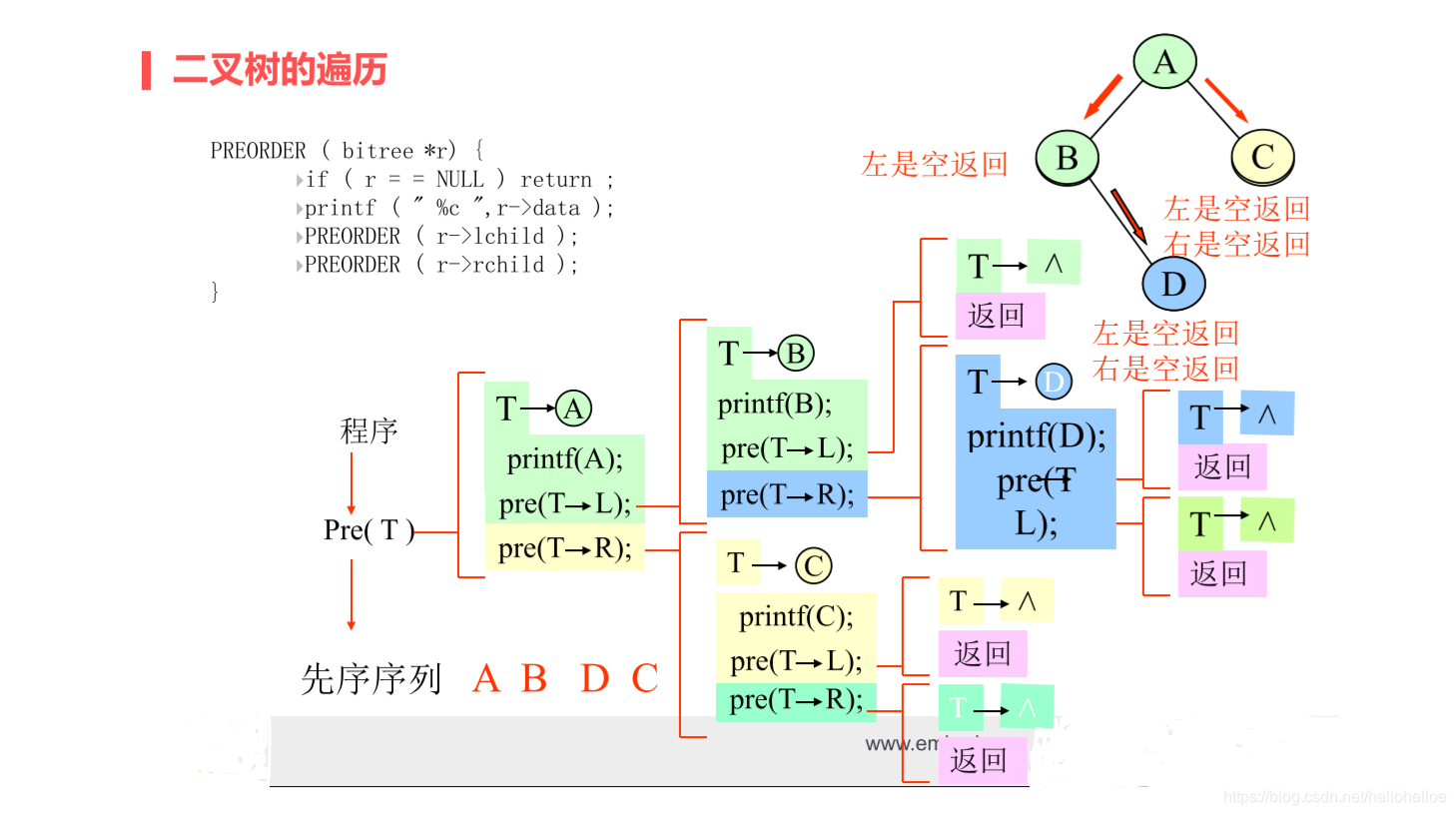
二叉树的遍历

由于二叉树的递归性质，遍历算法也是递归的。
三种遍历方式： 先序遍历、中序遍历、后序遍历。

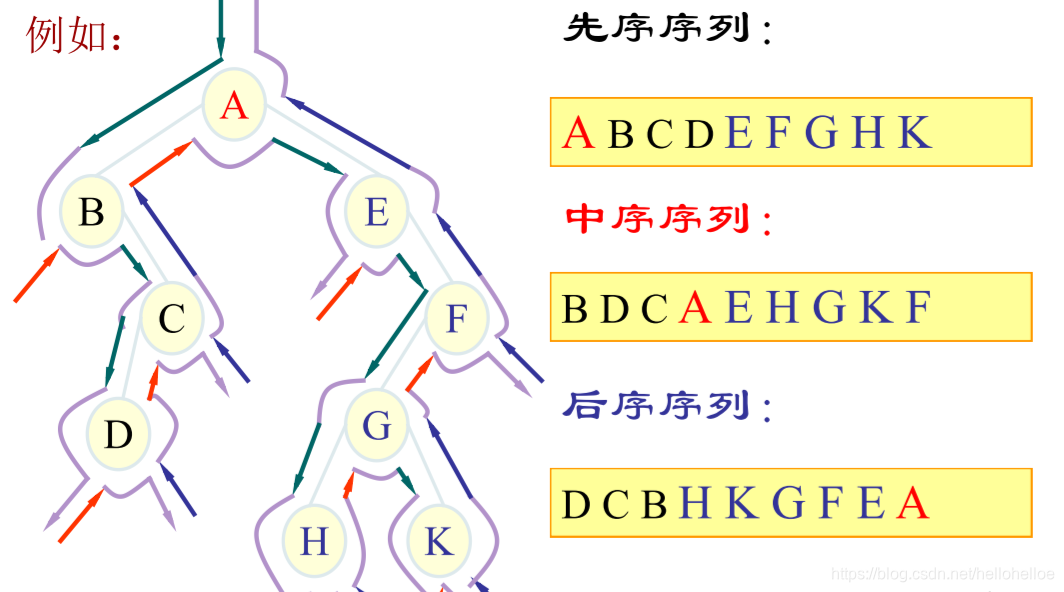
先序遍历

void pre_order(btree_t T)//前序
{
	//空则不遍历
	if(NULL == T)
	{
		return ;
	}

	//非空才遍历
	printf("%c", T->data);//根
	pre_order(T->lchild);//左子树
	pre_order(T->rchild);//右子树

}

中序遍历

void in_order(btree_t T)//中序
{
	//空则不遍历
	if(NULL == T)
	{
		return ;
	}

	//非空才遍历
	in_order(T->lchild);//左子树
	printf("%c", T->data);//根
	in_order(T->rchild);//右子树

	return ;
	
}

后序遍历

void post_order(btree_t T)//后序
{
	//空则不遍历
	if(NULL == T)
	{
		return ;
	}

	//非空才遍历
	post_order(T->lchild);//左子树
	post_order(T->rchild);//右子树
	printf("%c", T->data);//根

	return ;

}

层序遍历

该图来自mooc浙江大学数据结构课程

void Levelorder ( btree_t T )
{
	if ( !T ) return; /* 若是空树则直接返回 */
	
    btree_t Temp;
    sequeue *Q = createSeQueue(); /* 创建空队列Q */
    
    inSeQueue( Q, T );
    while ( !isEmptySeQueue(Q) ) 
	{
        OutSeQueue( Q, &Temp );
        printf("%c ", Temp->data); /* 访问取出队列的结点 */
        if ( Temp->lchild )   
			inSeQueue( Q, Temp->lchild );
        if ( Temp->rchild )  
			inSeQueue( Q, Temp->rchild );
    }
}

测试

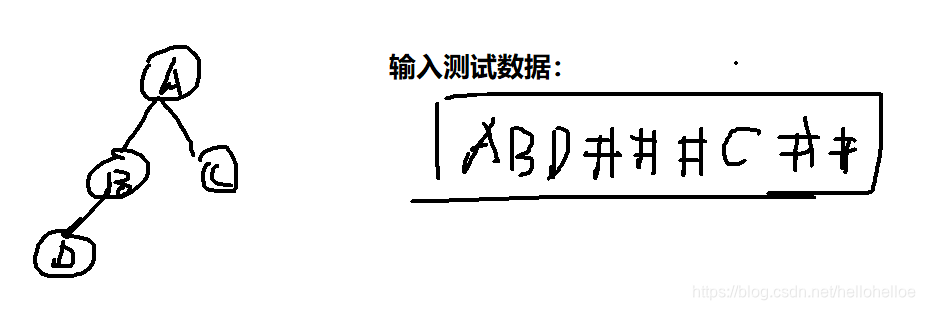
	btree_t T = createBtree();
	if(NULL == T)
	{
		printf("创建二叉树失败");
		return -1;
	}

	printf("pre: ");
	pre_order(T);
	printf("\n");

	printf("in: ");
	in_order(T);
	printf("\n");

	printf("post: ");
	post_order(T);
	printf("\n");

    return 0;

先序 中序 后序的非递归遍历算法

利用堆栈

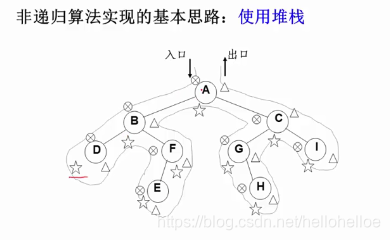
沿着如图所示路径遍历。
先序遍历就是在第一次遇到结点的时候输出，中序在第二次遇到的时候输出，后序是在第三次遇到的时候输出。

void preOder(btree_t T)
{
	seqstack * s = (seqstack *)malloc(sizeof(seqstack));//创建空栈
	
	while(T || !isEmpty(s)) 
	{
		while(T)
		{
			push(s, T);	//第一次碰到，将该结点指针入栈，并输出其数据
			printf("%c", T->data);
			T = T->lchild;//T指向T的左孩子 
		}
		
		if(!isEmpty(s))	//出栈，直到栈为空 
		{
			T = pop(s);	//第二次碰到，出栈该结点 
			
			T = T->rchild;			
		}
	}
}

void inOder(btree_t T)
{
	seqstack * s = (seqstack *)malloc(sizeof(seqstack));//创建空栈
	
	while(T || !isEmpty(s)) 
	{
		while(T)
		{
			push(s, T);	//第一次碰到，将该结点指针入栈
			T = T->lchild;//T指向T的左孩子 
		}
		
		if(!isEmpty(s))	//出栈，直到栈为空 
		{
			T = pop(s);	//第二次碰到，出栈该结点，并输出其数据 
			printf("%c", T->data);
			T = T->rchild;			
		}
	}
}

后序

void PostOrderTraversal(Bintree BT)
{
    Bintree T=BT;
    Bintree flag=NULL;//flag记录结点是否已被访问过
    Bintree top;
    Stack S=CreateStack(MaxSize);
    while(T || !IsEmpty(S))
    {
        while(T)
        {
            push(S,T);
            T=T->Left;
        }             //一路向左，将沿途结点压栈
        top=GetTop(S);        //获取栈顶元素，此时不出栈
        if(top->Right==NULL || top->Right==flag)  //此时top的左子树在上一个while循环中已访问过。当top的右子树为空或已访问过时打印top结点
        {
            printf("%5d",top->Data);
            flag=pop(s);    //用flag记录这个元素，表示已访问
        }
        else
            T=top->Right;       //若top的右子树没有被访问过，则将其当做一颗新二叉树访问
    }
}

网上看到一个很有意思的程序，也分享一下：

void PostOrderTraversal( BinTree BT )
 {   
     BinTree T =BT;   
     Stack S = CreatStack( MaxSize ); 
     Stack Q = CreatStack( MaxSize );
     while( T || !IsEmpty(S) )
    {  
       while(T)
       { 
         Push(S,T);  
           Push(Q,T);
         T = T->Right;
        }          //向右将沿途结点一路压栈
       if(!IsEmpty(S))
       {  
         T = Pop(S);
         T = T->Left; //转向左子树
        }   
   }  
   while( !IsEmpty(Q) )
    { 
      T = Pop(Q);
      printf(“%5d”, T->Data); 
    }  
}