主成分分析（PCA）与数据白化

matlab 实例

1.图像加载 12x12 的patch，共10000个，转换为 144x10000的矩阵，即数据是144维

x = sampleIMAGESRAW();
 
随机显示200个图像块，如下图：

2.零均值化

meanVal = mean(x);
x = bsxfun(@minus,x,meanVal);
 
此时 x
 为零均值数据

3.求协方差矩阵，并对协方差矩阵进行奇异值分解，再对数据进行特征向量投影

xRot = zeros(size(x)); 
[u,d] = svd(x*x'/size(x,2)); 
xRot = u' * x;
 
4.PCA 检测，计算协方差矩阵

covar = zeros(size(x, 1)); 
covar = xRot*xRot'/size(xRot,2);
 
此时的协方差矩阵为144x144的矩阵，显示为图像如下：

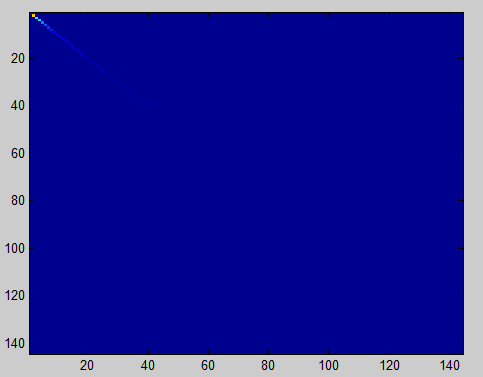
对角线为数据的自相关，也就是方差，值最大，所以颜色最亮，两边为协方差，值比较小，故颜色较暗，这里为蓝色。

5. 寻找能够保留90%方差的最小 k
 值

k = 0; 
dVal = diag(d); % 列向量
sumDVal = sum(dVal);
kP = 0;
while kP<0.9
    k = k+1;
    kP = sum(dVal(1:k)) / sumDVal;
end
 
此时 k为43，当设置为保留 99% 的方差时，k为116.

6. PCA降维

xHat = zeros(size(x));  
xHat = u(:,1:k) * xRot(1:k,:);

将 144维的数据降维到43维，并用43维数据还原图像如下：

7. PCA白化与规则化

epsilon = 0.1;
xPCAWhite = zeros(size(x));
xPCAWhite =  bsxfun(@rdivide,xRot,sqrt((dVal+epsilon)));

8. 检测PCA白化是否正确，计算协方差矩阵并显示

covar = xPCAWhite * xPCAWhite' / size(xPCAWhite,2);
 
白化后的协方差矩阵图像如下：

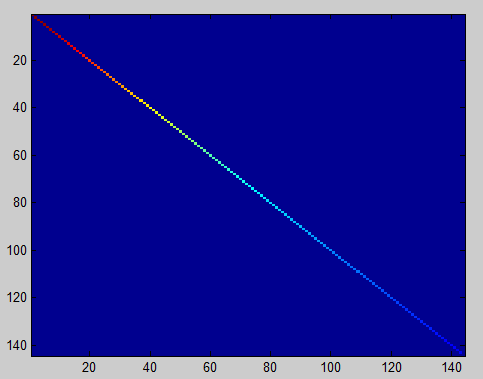
如果没有进行规则化，也就是我们将 ϵ
 设置为0，此时白化后的协方差矩阵如下图：

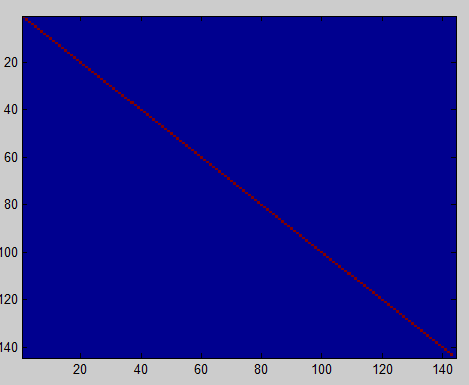
9.ZCA白化

xZCAWhite = zeros(size(x));
xZCAWhite = u*xPCAWhite;
 
ZCA白化后图像如下：