0-1背包

问题：

给定n种物品和一背包。物品i的重量是wi,其价值为vi,背包的容量为C。问：应该如何选择装入背包的物品，使得装入背包中的物品总价值最大

分析：

Xi表示第i物品,用1表示选了该物品，用0表示未选该产品，那么Xi*vi就是所选物品的价值，求和后就是选了的总价值。第二个条件就是：我们所选的总物件重量不能超过背包容量

综上我们得到公式：

 

方案

方案一：从头部减少

将第一个物品去掉，剩下X={x2,x3,....xn};

那么背包容量就需要去掉x1,就用算从x2到xn的重量和，并且最大的价值也要从x2到xn算起（从头部缩短问题规模）

Sum(Wi*xi)<=c-w1 *x1；Max（sum(vi,xi)) ； i=2,3,.....n

 

等等等等一直到n结束，此时当等于n时就是问题规模就为1

设计：

1.用m表示最优解，有两个因素 物品的数量(i) 和当前背包的能够存放的重量(j)

注意：i是一个区间：i,i+1,i+2,....，n;

2.设计基本元素后，我们从最简单情况开始，当i==n时表示只有一个元素，我们只需要判断他的重量与当前背包容量，如果小于当前容量则可以存放，如果大于则不能

即 j>= w[n]? v[n]:0;

3.接下来就到了下一个，如果当前背包容量小于你所选的那个物品重量，那么我们就第i+1开始选，跳过当前物品。否则：分两种情况：如果选择当前物品，则对应的当前背包容量减去当前物品重量，价值加上当前物品价值，如果不选择，则从第i+1开始选，需要对这两种情况的价值进行比较，去最大的结果

得到状态转移方程

 

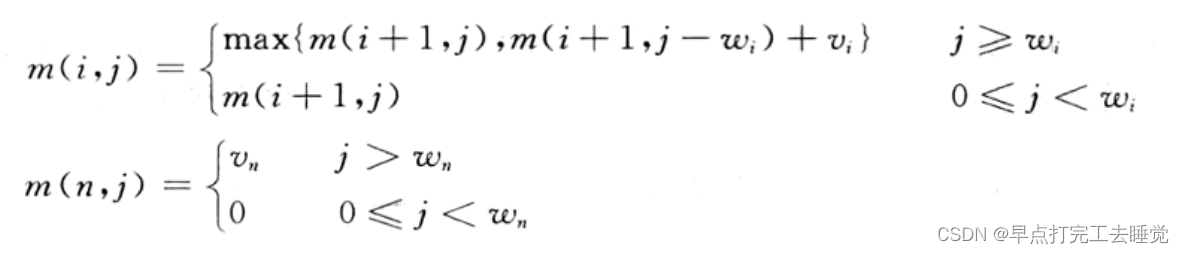
编写程序：

第一：递归方法

完全按照动归方程

int Knapsance(int V[], int W[], int i, int n, int j) {
    if (i == n) {
        if (j >= W[i]) {
            return V[i];
        }
        else {
            return 0;
        }
    }
    else {
        if (j < W[i]) {
            return Knapsance(V, W, i + 1, n, j);
        }
        else {
            int v1 = Knapsance(V, W, i + 1, n, j);
            int v2 = Knapsance(V, W, i + 1, n, j - W[i]) + V[i];
            if (v1 > v2) {
                return v1;
            }
            else {
                return v2;
            }
        }
    }
}

第二：非递归（进一步优化问题）

需要有一个空间去存储值

 

先判断第五个是否能放，然后依次判断4 3 2 1

int NiceKnapsance(int V[], int W[], int  n, int c,vector<vector<int>>&m) {
    for (int j = 1; j <= c; ++j) {
        m[n][j] = j >= W[n] ? V[n] : 0;
    }
    Printvector(m);
    for (int i = n - 1; i >= 1; --i) {
        for (int j = 1; j <= c; ++j) {
            if (j < W[i]) {
                m[i][j] = m[i + 1][j];
            }
            else {
                m[i][j] = std::max(m[i + 1][j], m[i + 1][j - W[i]] + V[i]);
            }
        }
        Printvector(m);
    }
    return  m[1][c];
}

结果如图所示

方案二：从尾部减少

在头删那块我们用i来表示从x1一直到xn;

在尾部这：判断最后一个是否选取后，那么我们应该是从1到n-1即i-1

动态方程与头部删除唯一不同的就在于i-1还是i+1

递归：

int Knapsance2(int V[], int W[], int i, int j) {
	if (i == 1) {
		if (j >= W[i]) {
			return V[i];
		}
		else {
			return 0;
		}
	}
	else {
		if (j < W[i]) {
			return Knapsance2(V, W, i - 1, j);
		}
		else {
			int v1 = Knapsance2(V, W, i - 1, j);
			int v2 = Knapsance2(V, W, i - 1,  j - W[i]) + V[i];
			if (v1 > v2) {
				return v1;
			}
			else {
				return v2;
			}
		}
	}
}

非递归

int NiceKnapsance_2(int V[], int W[], int  n, int c, vector<vector<int>>& m) {

	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= c; j++) {

			if (j < W[i]) {
				m[i][j] = m[i - 1][j];
			}
			else {
				int x1 = m[i - 1][j];
				int x2 = m[i - 1][j - W[i]] + V[i];
				if (x1 > x2) {
					m[i][j] = x1;
				}
				else {
					m[i][j] = x2;
				}
			}
		}
			Printvector(m);
		}
		return m[n][c];
	
}

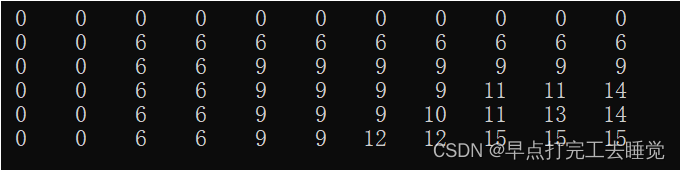
综上我们不难发现，无论是从头开始切还是从尾部开始切所得到的最大价值是一样的，但是他们的划分方法不同，导致矩阵每一个元素不同