bzoj2007 【省选基础 图论 平面图转对偶图】[Noi2010]海拔

题目传送门：http://43.140.204.8:666/p/75

[NOI2010] 海拔

题目描述

YT 市是一个规划良好的城市，城市被东西向和南北向的主干道划分为 $n\times n$ 个区域。简单起见，可以将 YT 市看作 一个正方形，每一个区域也可看作一个正方形。从而，YT 城市中包括 $(n+1)\times (n+1)$ 个交叉路口和 $2n\times (n+1)$ 条双向道路（简称道路），每条双向道路连接主干道上两个相邻的交叉路口。下图为一张 YT 市的地图（$n=2$），城市被划分为 $2\times 2$ 个区域，包括 $3\times 3$ 个交叉路口和 $12$ 条双向道路。

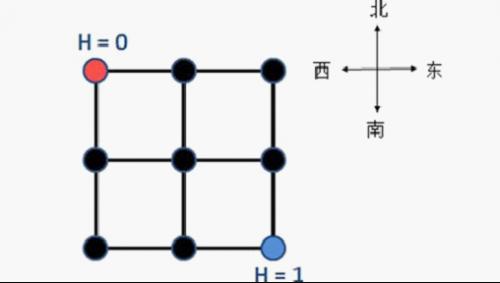
小 Z 作为该市的市长，他根据统计信息得到了每天上班高峰期间 YT 市每条道路两个方向的人流量，即在高峰期间沿着该方向通过这条道路的人数。每一个交叉路口都有不同的海拔高度值，YT 市市民认为爬坡是一件非常累的事情，每向上爬 $h$ 的高度，就需要消耗 $h$ 的体力。如果是下坡的话，则不需要耗费体力。因此如果一段道路的终点海拔减去起点海拔的值为 $h$（注意 $h$ 可能是负数），那么一个人经过这段路所消耗的体力是 max ⁡ { 0 , h } \max\{0, h\} max{0,h}。

小 Z 还测量得到这个城市西北角的交叉路口海拔为 $0$，东南角的交叉路口海拔为 $1$（如上图所示），但其它交叉路口的海拔高度都无法得知。小 Z 想知道在最理想的情况下（即你可以任意假设其他路口的海拔高度），每天上班高峰期间所有人爬坡消耗的总体力和的最小值。

输入格式

第一行包含一个整数 $n$。

接下来 $4n(n+1)$ 行，每行包含一个非负整数分别表示每一条道路每一个方向的人流量信息。

输入顺序：$n(n+1)$个数表示所有从西到东方向的人流量，然后 $n(n+1)$ 个数表示所有从北到南方向的人流量，$n(n+1)$ 个数表示所有从东到西方向的人流量，最后是 $n(n+1)$ 个数表示所有从南到北方向的人流量。对于每一个方向，输入顺序按照起点由北向南，若南北方向相同时由西到东的顺序给出（参见样例输入）。

输出格式

仅包含一个数，表示在最理想情况下每天上班高峰期间所有人爬坡所消耗的总体力和（即总体力和的最小值），结果四舍五入到整数。

样例 #1

样例输入 #1

1
1
2
3
4
5
6
7
8

样例输出 #1

3

提示

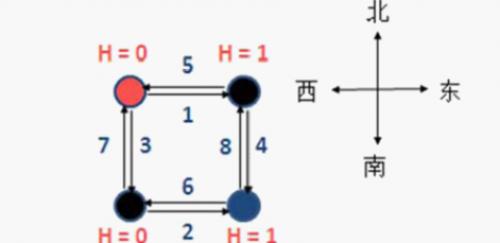
数据范围

• 对于 $20\%$ 的数据：$n\le 3$；
• 对于 $50\%$ 的数据：$n\le 15$；
• 对于 $80\%$ 的数据：$n\le 40$；
• 对于 $100\%$ 的数据：$1\le n\le 500$，$0\le \text{流量}\le 10^6$ 且所有流量均为整数。

一句话题解

我们可以想办法求出最小割。而当长度等于容量时，最小割的容量等于最短路的长度，我们就可以跑最短路来实现了。

具体实现

#include <algorithm>
#include <cstdio>
#include <cstring>
#include <queue>
#define N 255555
using namespace std;
struct edge
{
    int t, next, v;
} ed[N * 23];
int n, s[555][555][4], cnt, head[N], s1 = 254444, t = 254445, dis[N], vis[N];
inline int getid(int x, int y)
{
    if (x <= 0 || y <= 0)
        return s1;
    if (x >= n || y >= n)
        return t;
    return x * (n - 1) - n + 1 + y;
}   //
void adde(int f, int t, int v)
{
    ed[++cnt] = (edge){t, head[f], v};
    head[f]   = cnt;
}
void dijkstra(int s)
{
    priority_queue<pair<int, int>> s1;
    memset(dis, 0x3f, sizeof(dis));
    dis[s] = 0;
    s1.push(make_pair(0, s));
    while (!s1.empty())
    {
        pair<int, int> s2 = s1.top();
        s1.pop();
        int s = s2.second;
        if (vis[s])
            continue;
        vis[s] = 1;
        for (int i = head[s]; i; i = ed[i].next)
            if (dis[ed[i].t] > dis[s] + ed[i].v)
                dis[ed[i].t] = dis[s] + ed[i].v, s1.push(make_pair(-dis[ed[i].t], ed[i].t));
    }
}
int main()
{
    scanf("%d", &n);
    n++;
    for (int i = n; i >= 1; i--)
        for (int j = 1; j < n; j++)
            scanf("%d", &s[i][j][0]), adde(getid(i - 1, j), getid(i, j), s[i][j][0]);
    for (int i = n - 1; i >= 1; i--)
        for (int j = 1; j <= n; j++)
            scanf("%d", &s[i][j][1]), adde(getid(i, j - 1), getid(i, j), s[i][j][1]);
    for (int i = n; i >= 1; i--)
        for (int j = 1; j < n; j++)
            scanf("%d", &s[i][j][2]), adde(getid(i, j), getid(i - 1, j), s[i][j][2]);
    for (int i = n - 1; i >= 1; i--)
        for (int j = 1; j <= n; j++)
            scanf("%d", &s[i][j][3]), adde(getid(i, j), getid(i, j - 1), s[i][j][3]);
    dijkstra(s1);
    printf("%d\n", dis[t]);
}

AD

$$\text{Lvshu OJ }\text{，大量高质量题目等着你，点击这里马上注册。}$$