关于上篇文章的一些推广习题的讨论

原创 已于 2025-01-03 11:48:23 修改 · 658 阅读 · 17 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#c++ #算法 #数据结构 #链表 #排序算法

于 2025-01-03 11:40:46 首次发布

第二章 数据结构

问题1：链表所表示的元素是否有序?如有序，则有序性体现于何处?链表所表示的元素是否一定要在物理上是相邻的?有序表的有序性又如何理解?

答：

链表是一种常见的数据结构，用于存储一系列元素。链表中的元素可以是有序的，也可以是无序的，这取决于链表的类型和用途。下面是对您问题的一些解答：

  1. 链表所表示的元素是否有序？
    • 这取决于链表的类型。链表可以分为单链表、双链表、循环链表等，它们可以是有序的也可以是无序的。例如，一个单链表可以表示一个有序序列，其中每个节点包含数据和指向下一个节点的指针。
  2. 如有序，则有序性体现于何处？
    • 如果链表是有序的，那么有序性通常体现在元素的排列顺序上。在有序链表中，元素按照某种顺序（如升序或降序）排列，并且每个节点的后继节点在顺序上是连续的。
  3. 链表所表示的元素是否一定要在物理上是相邻的？
    • 不一定。链表中的元素在物理上不需要是相邻的。链表是一种逻辑上连续的数据结构，每个元素（节点）包含数据和指向下一个元素的指针。这意味着即使在物理存储上元素是分散的，它们也可以通过指针逻辑上连接起来。
  4. 有序表的有序性如何理解？
    • 有序表的有序性是指表中元素的排列顺序遵循某种规则或标准。例如，在有序数组中，元素可能是按照数值大小排序的；在有序链表中，元素可能按照某种顺序链接起来。有序表的有序性允许我们进行更高效的搜索、插入和删除操作，因为我们可以利用元素的顺序来减少不必要的比较和操作。

问题2：设顺序表L是递增有序表，试写一算法，将 x插入到L中并使L仍是递增有序表。

#include <stdio.h>

#define MAX_SIZE 100  // 定义顺序表的最大长度

// 顺序表结构
typedef struct {
    int data[MAX_SIZE];  // 存储空间
    int length;         // 当前长度
} SeqList;

// 插入元素的函数
int Insert(SeqList *L, int x) {
    int i, j;
    // 寻找插入位置
    for (i = 0; i < L->length; i++) {
        if (L->data[i] > x) {
            break;
        }
    }
    // 元素后移，为新元素腾出空间
    for (j = L->length; j > i; j--) {
        L->data[j] = L->data[j - 1];
    }
    // 插入新元素
    L->data[i] = x;
    // 顺序表长度加1
    L->length++;
    return 0;
}

// 打印顺序表的函数
void PrintList(SeqList L) {
    for (int i = 0; i < L.length; i++) {
        printf("%d ", L.data[i]);
    }
    printf("\n");
}

int main() {
    SeqList L;
    L.length = 0;  // 初始化顺序表长度为0

    // 假设顺序表L已经有一些元素，这里我们手动添加一些
    Insert(&L, 1);
    Insert(&L, 3);
    Insert(&L, 5);
    Insert(&L, 7);

    printf("Original list: ");
    PrintList(L);

    int x = 4;  // 要插入的元素
    Insert(&L, x);

    printf("List after inserting %d: ", x);
    PrintList(L);

    return 0;
}

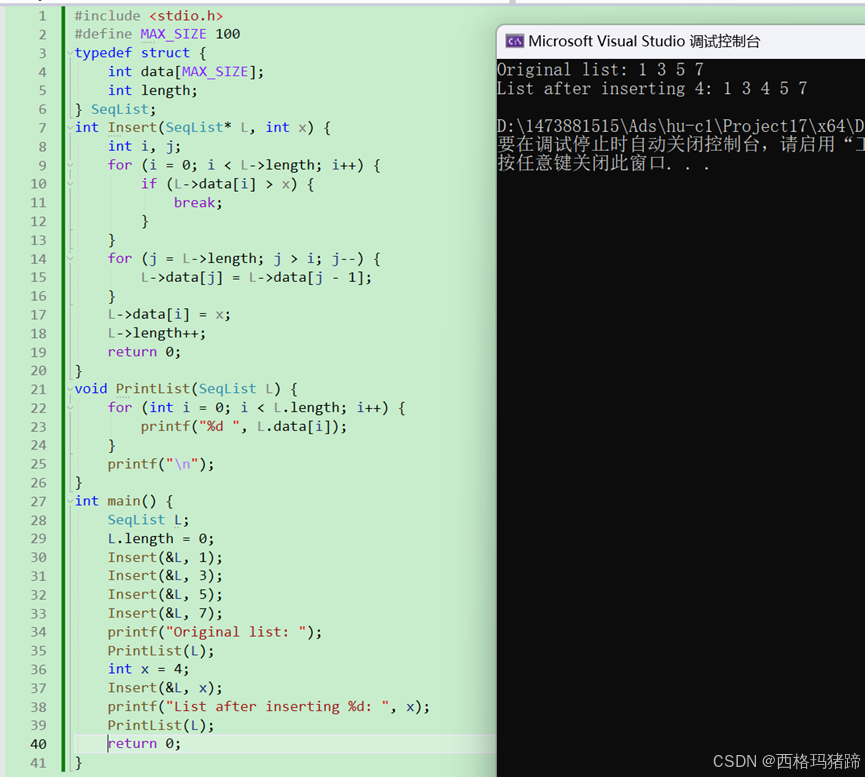
这个程序首先定义了一个顺序表结构 SeqList，其中包含一个整数数组 data 用于存储元素，以及一个整数 length 用于记录当前顺序表的长度。Insert 函数用于将元素 x 插入到顺序表 L 中的正确位置，以保持顺序表的递增有序性。PrintList 函数用于打印顺序表中的所有元素。

在 main 函数中，我们初始化了一个顺序表 L，然后添加了一些元素，并打印了原始顺序表。接着，我们插入了一个新元素 x，并再次打印了插入新元素后的顺序表。

问题3：写一求单链表的结点数目ListLength(L)的算法。

#include <stdio.h>
#include <stdlib.h>

// 定义单链表的节点结构
typedef struct Node {
    int data;  // 节点数据
    struct Node *next;  // 指向下一个节点的指针
} Node;

// 计算单链表节点数目的函数
int ListLength(Node *L) {
    int count = 0;  // 节点计数器
    Node *current = L;  // 当前节点指针

    // 遍历链表，直到当前节点为NULL
    while (current != NULL) {
        count++;  // 增加节点计数
        current = current->next;  // 移动到下一个节点
    }

    return count;  // 返回节点数目
}

// 创建新节点的函数
Node *CreateNode(int data) {
    Node *newNode = (Node *)malloc(sizeof(Node));  // 分配新节点的内存
    if (newNode == NULL) {
        printf("Memory allocation failed.\n");
        exit(1);
    }
    newNode->data = data;  // 设置节点数据
    newNode->next = NULL;  // 设置指针为NULL
    return newNode;
}

// 将新节点添加到链表末尾的函数
void AppendNode(Node **L, int data) {
    Node *newNode = CreateNode(data);  // 创建新节点
    if (*L == NULL) {
        *L = newNode;  // 如果链表为空，新节点即为头节点
    } else {
        Node *current = *L;  // 当前节点指针
        while (current->next != NULL) {
            current = current->next;  // 移动到链表末尾
        }
        current->next = newNode;  // 将新节点添加到末尾
    }
}

// 打印链表的函数
void PrintList(Node *L) {
    Node *current = L;  // 当前节点指针
    while (current != NULL) {
        printf("%d ", current->data);  // 打印节点数据
        current = current->next;  // 移动到下一个节点
    }
    printf("\n");
}

int main() {
    Node *L = NULL;  // 初始化链表为空

    // 向链表中添加一些节点
    AppendNode(&L, 1);
    AppendNode(&L, 3);
    AppendNode(&L, 5);
    AppendNode(&L, 7);

    printf("List: ");
    PrintList(L);

    int length = ListLength(L);  // 计算链表长度
    printf("List length: %d\n", length);

    return 0;
}

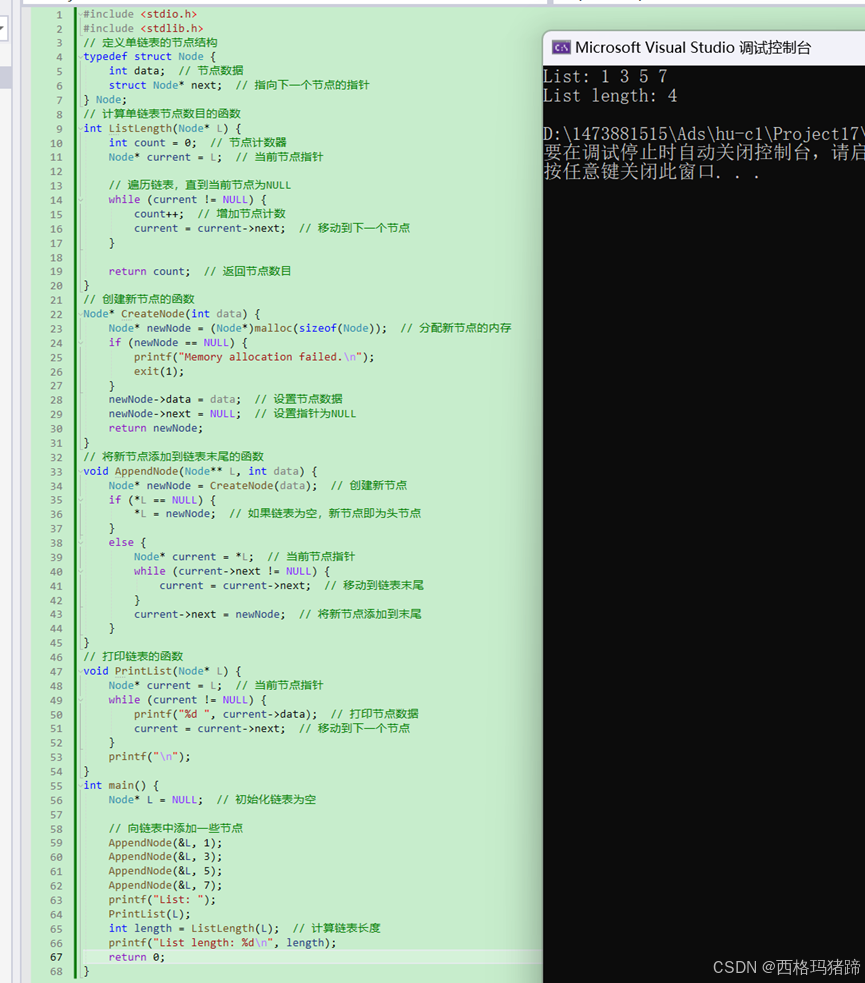
这个程序首先定义了一个单链表的节点结构 Node，其中包含一个整数 data 和一个指向下一个节点的指针 next。ListLength 函数用于计算单链表的节点数目，它通过遍历链表并计数节点来实现。CreateNode 函数用于创建一个新的节点，AppendNode 函数用于将新节点添加到链表的末尾，PrintList 函数用于打印链表中的所有节点。

在 main 函数中，我们初始化了一个空链表 L，然后向其中添加了一些节点，并打印了链表。接着，我们调用 ListLength 函数计算了链表的长度，并打印了结果。

问题4：写一算法将单链表中值重复的结点删除， 使所得的结果链表中所有结点的值均不相同。

#include <stdio.h>
#include <stdlib.h>
typedef struct Node {
    int data;
    struct Node* next;
} Node;
// 创建新节点的函数
Node* CreateNode(int data) {
    Node* newNode = (Node*)malloc(sizeof(Node));
    if (newNode == NULL) {
        printf("Memory allocation failed.\n");
        exit(1);
    }
    newNode->data = data;
    newNode->next = NULL;
    return newNode;
}
// 打印链表的函数
void PrintList(Node* L) {
    Node* current = L; // 初始化current为L
    while (current != NULL) {
        printf("%d ", current->data);
        current = current->next;
    }
    printf("\n");
}
// 删除重复节点的函数
void RemoveDuplicates(Node** L) {
    if (*L == NULL) {
        return; // 如果链表为空，不需要删除
    }

    Node* current = *L;
    while (current != NULL && current->next != NULL) {
        if (current->data == current->next->data) {
            Node* temp = current->next; // 保存要删除的节点
            current->next = current->next->next; // 从链表中移除重复节点
            free(temp); // 释放节点内存
        }
        else {
            current = current->next; // 移动到下一个节点
        }
    }
}
int main() {
    Node* L = NULL;  // 初始化链表为空

    // 向链表中添加一些节点，包括重复的值
    L = CreateNode(1);
    L->next = CreateNode(2);
    L->next->next = CreateNode(2);
    L->next->next->next = CreateNode(3);
    L->next->next->next->next = CreateNode(4);
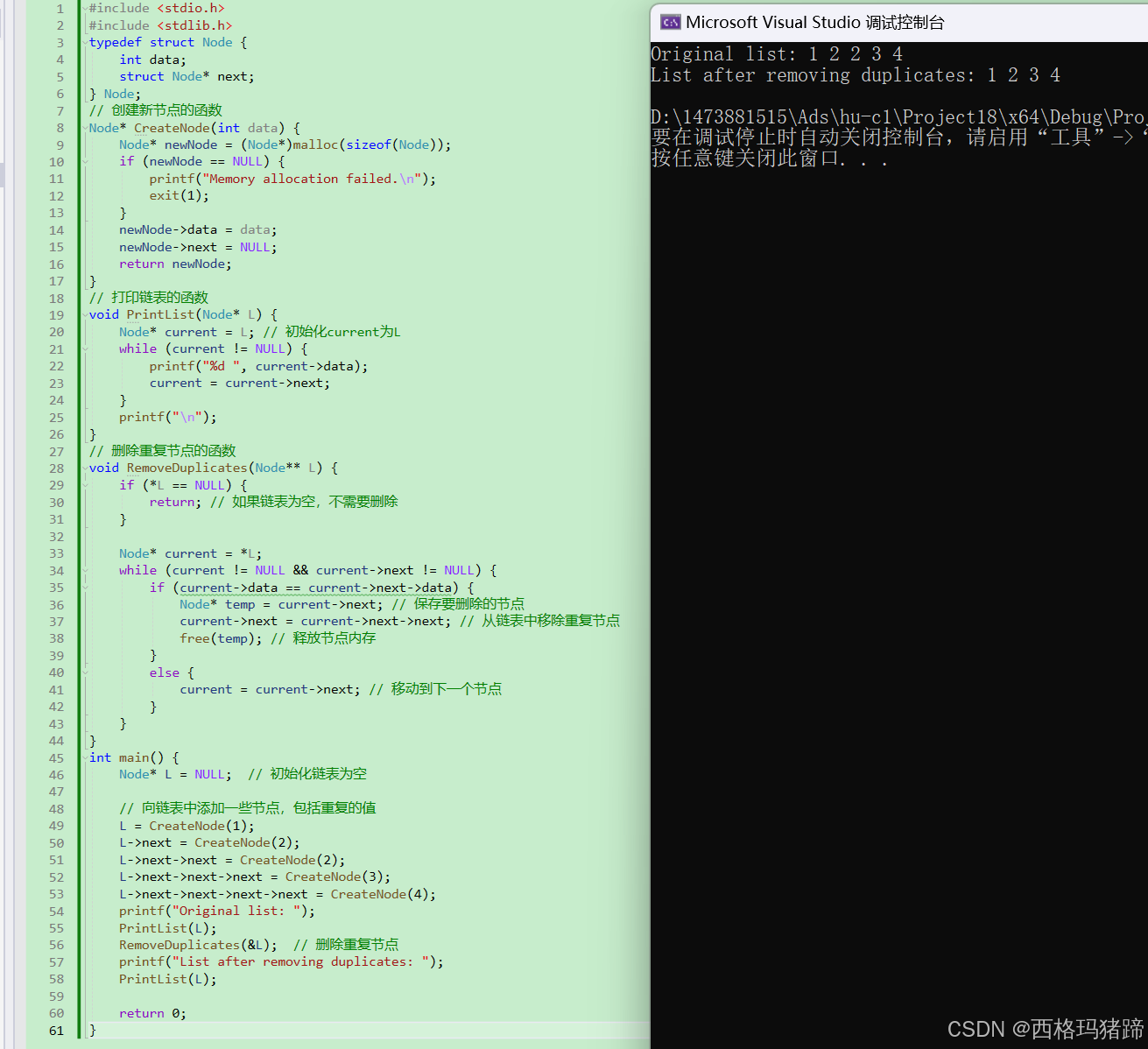
    printf("Original list: ");
    PrintList(L);
    RemoveDuplicates(&L);  // 删除重复节点
    printf("List after removing duplicates: ");
    PrintList(L);

    return 0;
}

下面是对代码中每个函数的简析：

  1. CreateNode 函数：

    • 这个函数用于创建一个新的链表节点。
    • 它接受一个整数 data 作为参数，分配一个新的节点，并将其数据域设置为 data。
    • 如果内存分配失败，它会打印一条错误消息并退出程序。
    • 成功创建的节点的 next 指针被初始化为 NULL。

  2. PrintList 函数：

    • 这个函数用于打印链表中的所有节点数据。
    • 它通过一个指针 current 遍历链表，从链表的头节点开始，直到 current 为 NULL。
    • 每次迭代都会打印当前节点的数据，然后移动到下一个节点。

  3. RemoveDuplicates 函数：

    • 这个函数用于删除链表中值重复的节点。
    • 它首先检查链表是否为空，如果为空，则直接返回。
    • 然后，它使用一个指针 current 遍历链表，检查当前节点的值是否与其后继节点的值相同。
    • 如果值相同，它会保存后继节点的地址到 temp，然后调整 current 的 next 指针以跳过重复的节点，并释放 temp 指向的节点内存。
    • 如果值不相同，current 指针就会移动到下一个节点。

  4. main 函数：

    • 这是程序的入口点。
    • 它首先初始化一个空链表 L。
    • 然后，通过调用 CreateNode 函数并链接新节点来构建链表，包括一些重复的值（例如，两个值为2的节点）。
    • 使用 PrintList 函数打印原始链表。
    • 调用 RemoveDuplicates 函数删除链表中的重复节点。
    • 最后，再次使用 PrintList 函数打印删除重复节点后的链表。

程序的输出将是原始链表和删除重复节点后的链表。然而，当前的 RemoveDuplicates 函数实现有一个问题：它只删除了相邻的重复节点。如果链表中有非相邻的重复节点，这个函数将无法删除它们。要删除所有重复的节点，需要一个更复杂的算法，例如使用一个哈希表来跟踪已经见过的值。

问题5：写一算法从一给定的向量A删除值在x到 y(x≤y)之间的所有元素(注意：x和y是给定 的参数，可以和表中的元素相同，也可以不同）

#include <stdio.h>

// 删除向量A中值在x到y之间的所有元素的函数
void RemoveElements(int A[], int size, int x, int y) {
    int i, j = 0; // j用于跟踪新数组的索引

    // 遍历数组
    for (i = 0; i < size; i++) {
        // 如果当前元素不在x到y的范围内，则将其保留
        if (A[i] < x || A[i] > y) {
            A[j++] = A[i]; // 将元素复制到新位置
        }
    }

    // 将数组截断到新的长度
    for (i = j; i < size; i++) {
        A[i] = 0; // 或者其他适当的清理操作
    }
}

// 打印数组的函数
void PrintArray(int A[], int size) {
    for (int i = 0; i < size; i++) {
        printf("%d ", A[i]);
    }
    printf("\n");
}

int main() {
    int A[] = {1, 3, 5, 7, 9, 11, 13, 15};
    int size = sizeof(A) / sizeof(A[0]);
    int x = 6, y = 12;

    printf("Original array: ");
    PrintArray(A, size);

    RemoveElements(A, size, x, y);

    printf("Array after removal: ");
    PrintArray(A, size);

    return 0;
}

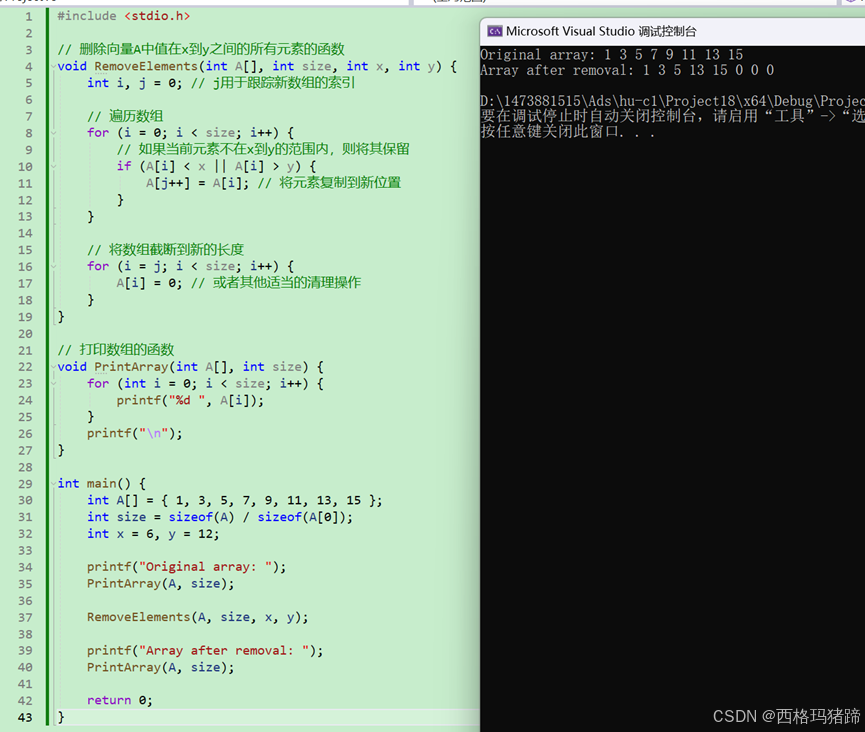
这个算法的工作原理如下：

  1. 使用两个索引 i 和 j，其中 i 用于遍历原始数组，j 用于在新位置存储不在 x 到 y 范围内的元素。
  2. 当遇到不在 x 到 y 范围内的元素时，将其复制到 j 指向的位置，并递增 j。
  3. 遍历完成后，原始数组中 j 之后的所有元素将被清零或进行其他适当的清理操作，以确保数组的其余部分不会包含无效数据。

请注意，这个算法假设数组 A 有足够的空间来存储所有不在 x 到 y 范围内的元素。如果数组可能需要动态调整大小，您可能需要使用动态内存分配。此外，如果数组中的元素是其他数据类型，您可能需要相应地调整比较操作。

问题6：设A和B是两个按元素值递增有序的单链表 ，写一算法将A和B归并为按按元素值递减有序的单链表C，试分析算法的时间复杂度。

#include <stdio.h>
#include <stdlib.h>

// 定义单链表的节点结构
typedef struct Node {
    int data;
    struct Node *next;
} Node;

// 创建新节点的函数
Node* CreateNode(int data) {
    Node *newNode = (Node *)malloc(sizeof(Node));
    if (newNode == NULL) {
        printf("Memory allocation failed.\n");
        exit(1);
    }
    newNode->data = data;
    newNode->next = NULL;
    return newNode;
}

// 向链表末尾添加节点的函数
void AppendNode(Node **L, int data) {
    Node *newNode = CreateNode(data);
    if (*L == NULL) {
        *L = newNode;
    } else {
        Node *current = *L;
        while (current->next != NULL) {
            current = current->next;
        }
        current->next = newNode;
    }
}

// 打印链表的函数
void PrintList(Node *L) {
    Node *current = L;
    while (current != NULL) {
        printf("%d ", current->data);
        current = current->next;
    }
    printf("\n");
}

// 归并两个递增有序链表为一个递减有序链表的函数
Node* MergeLists(Node *A, Node *B) {
    Node dummy;
    Node *tail = &dummy;
    dummy.next = NULL;

    while (A != NULL && B != NULL) {
        if (A->data > B->data) {
            tail->next = A;
            A = A->next;
        } else {
            tail->next = B;
            B = B->next;
        }
        tail = tail->next;
    }

    // 连接剩余的节点
    if (A != NULL) {
        tail->next = A;
    } else {
        tail->next = B;
    }

    // 反转链表
    Node *prev = NULL, *current = dummy.next, *nextNode;
    while (current != NULL) {
        nextNode = current->next;
        current->next = prev;
        prev = current;
        current = nextNode;
    }

    return prev;
}

int main() {
    Node *A = NULL;
    Node *B = NULL;

    // 构建递增有序链表A
    AppendNode(&A, 1);
    AppendNode(&A, 3);
    AppendNode(&A, 5);

    // 构建递增有序链表B
    AppendNode(&B, 2);
    AppendNode(&B, 4);
    AppendNode(&B, 6);

    printf("List A: ");
    PrintList(A);
    printf("List B: ");
    PrintList(B);

    Node *C = MergeLists(A, B);

    printf("Merged List C (in decreasing order): ");
    PrintList(C);

    return 0;
}

这个程序首先定义了一个单链表的节点结构 Node，然后提供了创建新节点、向链表末尾添加节点、打印链表和归并两个链表的函数。MergeLists 函数首先使用一个虚拟节点 dummy 来简化边界条件的处理，然后比较并连接两个链表的节点，最后反转链表以得到递减有序的结果。

在 main 函数中，我们构建了两个递增有序的链表A和B，然后调用 MergeLists 函数将它们归并为一个递减有序的链表C，并打印结果。

时间复杂度分析：

  1. 归并过程（MergeLists 函数）的时间复杂度是 O(n + m)，其中 n 和 m 分别是链表 A 和 B 的长度。这是因为我们需要遍历两个链表中的每个节点一次。
  2. 反转链表的过程（ReverseList 函数）的时间复杂度是 O(k)，其中 k 是链表 C 的长度。由于 k = n + m，所以反转操作的时间复杂度也是 O(n + m)。

第三章 图

问题1：

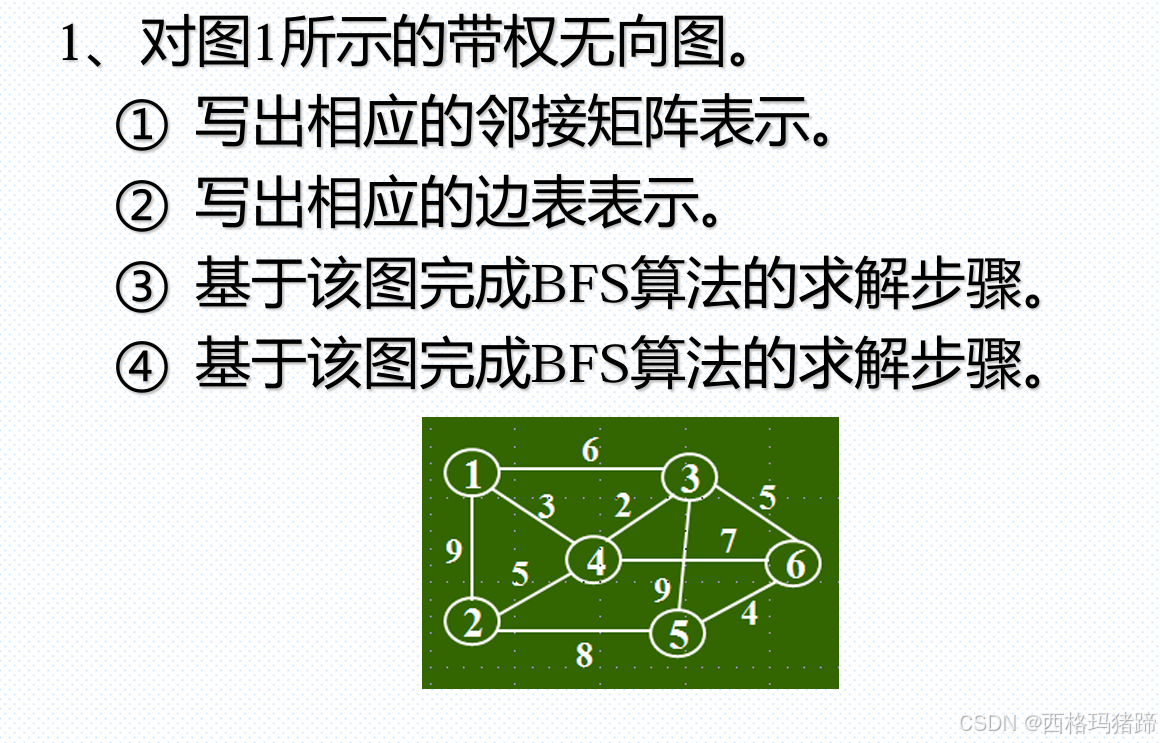
① 邻接矩阵表示

邻接矩阵是一个二维数组，用于表示图中顶点之间的连接关系。对于无向图，如果顶点 i 和顶点 j 之间有边，则矩阵的第 i 行第 j 列和第 j 行第 i 列的值是边的权重，否则为 0 或 ∞（表示不可达）。

对于给定的图，邻接矩阵如下（使用 ∞ 表示不可达）：

    1  2  3  4  5  6

1 [ 0, 9, 6, 3, ∞, ∞ ]

2 [ 9, 0, ∞, 5, 8, ∞ ]

3 [ 6, ∞, 0, 2, ∞, 5 ]

4 [ 3, 5, 2, 0, 9, 7 ]

5 [ ∞, 8, ∞, 9, 0, 4 ]

6 [ ∞, ∞, 5, 7, 4, 0 ]

② 边表表示

边表是一个列表，其中每个元素是一个边的描述，通常包括两个顶点和边的权重。对于给定的图，边表如下：

(1, 2, 9), (1, 3, 6), (1, 4, 3),

(2, 4, 5), (2, 5, 8),

(3, 4, 2), (3, 6, 5),

(4, 5, 9), (4, 6, 7)

③ 基于该图完成BFS算法的求解步骤

假设我们从顶点 1 开始进行广度优先搜索（BFS）：

  1. 初始化队列 Q 和访问数组 visited，将 1 加入 Q，标记为 visited。
  2. 从 Q 中取出 1，访问其所有未访问的邻居（2, 3, 4），将它们加入 Q 并标记为 visited。
  3. 从 Q 中取出 2，访问其未访问的邻居（5），将 5 加入 Q 并标记为 visited。
  4. 从 Q 中取出 3，访问其未访问的邻居（6），将 6 加入 Q 并标记为 visited。
  5. 从 Q 中取出 4，没有未访问的邻居。
  6. 从 Q 中取出 5，没有未访问的邻居。
  7. 从 Q 中取出 6，没有未访问的邻居。

BFS 完成后的访问顺序为：1, 2, 3, 4, 5, 6。

④ 基于该图完成DFS算法的求解步骤

假设我们从顶点 1 开始进行深度优先搜索（DFS）：

  1. 初始化栈 S 和访问数组 visited，将 1 压入 S，标记为 visited。
  2. 访问 1，将其所有未访问的邻居（2, 3, 4）压入 S 并标记为 visited。
  3. 访问 2，将其未访问的邻居（5）压入 S 并标记为 visited。
  4. 访问 5，将其未访问的邻居（6）压入 S 并标记为 visited。
  5. 访问 6，没有未访问的邻居，返回上一个节点。
  6. 返回到 5，没有其他未访问的邻居，返回上一个节点。
  7. 返回到 2，没有其他未访问的邻居，返回上一个节点。
  8. 返回到 1，访问其未访问的邻居（4），将 4 压入 S 并标记为 visited。
  9. 访问 4，没有未访问的邻居。

DFS 完成后的访问顺序可能为：1, 2, 5, 6, 4 或其他变体，具体取决于邻居的访问顺序。

问题2：

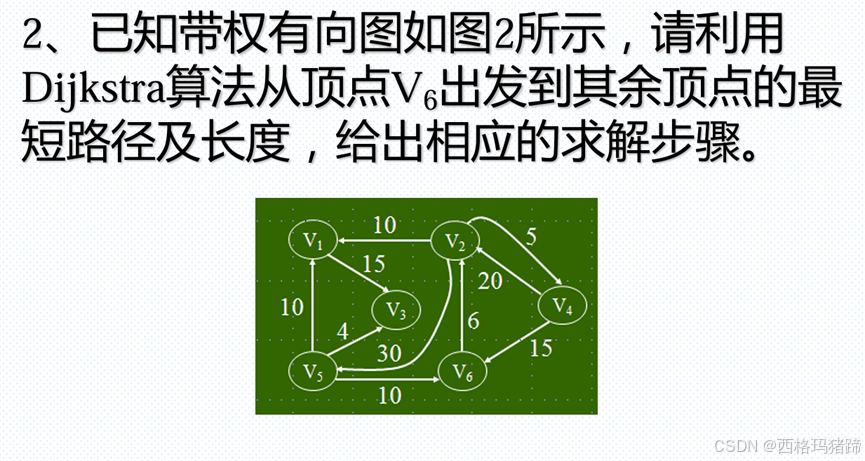
初始化：

  1. 设置V6到自身的最短距离为0，即dist[V6]=0dist[V6​]=0。
  2. 对于所有其他顶点Vi，初始化dist[Vi]dist[Vi​]为从V6​到Vi的直接距离（如果存在直接边）或无穷大（如果没有直接边）。
  3. 创建一个未访问顶点的集合，初始包含所有顶点。

迭代过程：

重复以下步骤直到所有顶点都被访问：

  1. 从未访问顶点中选择具有最小dist值的顶点u。
  2. 标记u为已访问。
  3. 更新u的所有未访问邻居v的dist值：

dist[v]=min⁡(dist[v],dist[u]+weight(u,v))

其中weight(u,v)是从u到v的边的权重。

应用到给定的图：

从 V6开始，我们有以下边和权重：

  • V6到V2​: 6
  • V6到V4​: 15
  • V6到V5​: 10

步骤 1: 初始化：

  • dist[V6]=0
  • dist[V1]=∞
  • dist[V2]=6
  • dist[V3]=∞
  • dist[V4]=15
  • dist[V5]=10

步骤 2: 迭代过程：

  1. 选择 V6V，更新邻居：
    • dist[V2]=6 (已更新)
    • dist[V4]=15 (已更新)
    • dist[V5]=10 (已更新)
  2. 选择 V2（最小 dist），更新邻居：
    • dist[V1]=16 (通过V2和边V1到V2的权重10)
    • dist[V3]=26 (通过V2和边V3到V2的权重20)
  3. 选择 V5，更新邻居：
    • dist[V1]=14 (通过V5​和边V5到V1的权重4)
  4. 选择 V4，更新邻居：
    • 没有更短的路径
  5. 选择 V1，更新邻居：
    • dist[V3]=29(通过V1和边V1到V3的权重15)
  6. 最后选择 V3，没有更新。

结果：

  • V1​: 最短路径长度 14，路径 V6→V5→V1
  • V2: 最短路径长度 6，路径 V6→V2
  • V3​: 最短路径长度 26，路径 V6→V2→V3 ​
  • V4: 最短路径长度 15，路径 V6→V4
  • V5: 最短路径长度 10，路径 V6→V5
  • 这些步骤和结果提供了从V6到图中所有其他顶点的最短路径和长度。

问题3：

Bellman-Ford算法是一种用于寻找图中所有顶点对之间最短路径的算法，特别是当图中可能存在负权重边时。以下是使用Bellman-Ford算法从顶点 V5出发到其余顶点的最短路径及长度的求解步骤：

初始化：

  1. 设置 V5到自身的最短距离为0，即 dist[V5]=0
  2. 对于所有其他顶点Vi，初始化dist[Vi]为无穷大（或一个非常大的数）。
  3. 创建一个布尔数组visited来跟踪每个顶点是否已经被更新过。

迭代过程：

重复以下步骤 V−1次，其中 V是顶点的数量：

对于每条边（u，v），如果dist[u]+weight(u,v)<dist[v]，则更新dist[v]为 dist[u]+weight(u,v)。

检测负权重循环：

在 V−1次迭代后，再次检查所有边。如果仍然可以更新 dist[v]，则图中存在负权重循环。

应用到给定的图：

从 V5 开始，我们有以下边和权重：

  • V5到V1​: 4
  • V5到V3​: 30
  • V5到V6​: 10

步骤 1:初始化：

  • dist[V5​]=0
  • dist[V1]=∞
  • dist[V2]=∞
  • dist[V3]=∞
  • dist[V4]=∞
  • dist[V6]=∞

步骤 2: 迭代过程：

  1. 第一次迭代：
    • 更新dist[V1]=4 (通过V5
    • 更新dist[V3]=34 (通过V5​)
    • 更新dist[V6]=10 (通过V5​)
  2. 第二次迭代：
    • 更新dist[V2]=14 (通过V6和边V6到V2的权重 6)
    • 更新dist[V3]=19 (通过V1和边V1到V3的权重 15)
  3. 第三次迭代：
    • 更新dist[V2]=13 (通过V3和边V3到V2的权重 20)
  4. 第四次迭代：
    • 没有更新

结果：

  • V1​: 最短路径长度 4，路径 V5→V1
  • V2: 最短路径长度 13，路径 V5→V3→V2
  • V3: 最短路径长度 19，路径 V5→V1→V3
  • V4: 最短路径长度 ∞，因为没有从 V5到 V4的路径
  • V6​: 最短路径长度 10，路径 V5→V6

这些步骤和结果提供了从V5到图中所有其他顶点的最短路径和长度。请注意，如果图中存在负权重循环，Bellman-Ford算法能够检测到这一点，但在本例中没有负权重循环。

问题4：

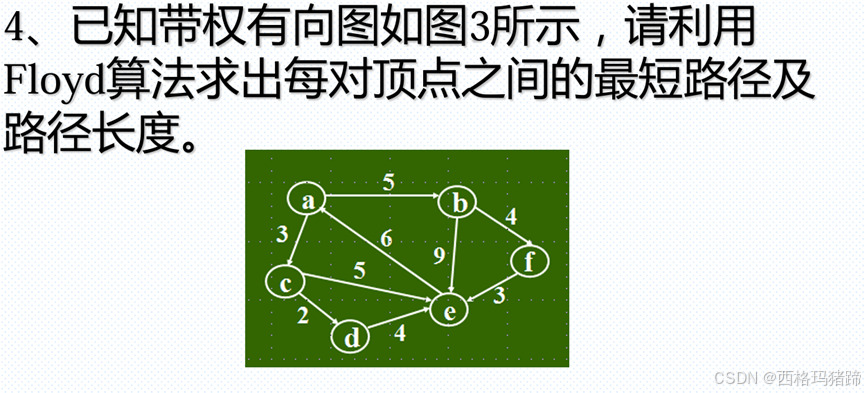
初始化：

  1. 创建一个距离矩阵 dist，其中 dist[i][j] 表示顶点 i 到顶点 j 的直接距离。如果 i 和 j 之间没有直接的边，那么 dist[i][j] 应该是无穷大（或一个非常大的数）。
  2. 创建一个前驱节点矩阵 next，用于记录路径。如果 i 到 j 有直接的边，那么 next[i][j] 就是 j；如果没有直接的边或者 i 等于 j，那么 next[i][j] 就是 null 或 i。

迭代过程：

对于每一个顶点 k：

  1. 更新所有顶点对 (i, j) 的距离和前驱节点：
    • 如果 dist[i][k] + dist[k][j] < dist[i][j]，则更新 dist[i][j] 为 dist[i][k] + dist[k][j]。
    • 同时更新 next[i][j] 为 next[i][k]。

应用到给定的图：

根据图中的边和权重，初始化距离矩阵和前驱节点矩阵：

dist = {

  {0, 5, 3, ∞, 6, ∞},

  {∞, 0, ∞, 9, ∞, 4},

  {∞, ∞, 0, 2, 5, ∞},

  {∞, ∞, ∞, 0, 4, ∞},

  {∞, ∞, ∞, ∞, 0, 3},

  {∞, ∞, ∞, ∞, ∞, 0}

}

next = {

  {a, b, c, null, e, null},

  {null, b, null, e, null, f},

  {null, null, c, d, e, null},

  {null, null, null, d, null, null},

  {null, null, null, null, e, f},

  {null, null, null, null, null, f}

}

迭代更新：

对于每一个顶点 k，更新 dist 和 next。这里我们只展示更新后的距离矩阵，因为前驱节点矩阵的更新过程类似，但更复杂。

  1. 更新 k=a：
    • 没有变化，因为 a 到其他顶点的直接距离已经是最短的。
  2. 更新 k=b：
    • dist[c][f] 更新为 dist[c][b] + dist[b][f] = 3 + 4 = 7。
  3. 更新 k=c：
    • dist[a][d] 更新为 dist[a][c] + dist[c][d] = 3 + 2 = 5。
    • dist[b][d] 更新为 dist[b][c] + dist[c][d] = ∞ + 2 = 2（因为 b 到 c 没有直接边，所以这个更新不会发生）。
  4. 更新 k=d：
    • dist[a][e] 更新为 dist[a][d] + dist[d][e] = 5 + 4 = 9。
  5. 更新 k=e：
    • dist[b][e] 更新为 dist[b][e] = 9（更新为直接距离）。
    • dist[c][e] 更新为 dist[c][e] = 5（更新为直接距离）。
  6. 更新 k=f：
    • 没有变化，因为 f 到其他顶点的直接距离已经是最短的。

结果：

最终的距离矩阵 dist 将包含所有顶点对之间的最短路径长度。前驱节点矩阵 next 可以用于重建最短路径。

评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值