资料:
- https://download.youkuaiyun.com/download/ccgcccccc/12126611 课程作业,包括空白作业和自己完成的作业版本
- Jupyter notebook入门教程(上) Jupyter notebook入门教程(下)
test = "Hello World"
print ("test: " + test)
import numpy as np
def sigmoid(x):
s = 1/(1 + np.exp(-x))
return s
x = np.array([1, 2, 3])
sigmoid(x)
def sigmoid_derivative(x):
s = 1/(1 + np.exp(-x))
ds = s*(1-s)
return ds
x = np.array([1, 2, 3])
print ("sigmoid_derivative(x) = " + str(sigmoid_derivative(x)))
def image2vector(image):
v = image.reshape(image.shape[0]*image.shape[1]*image.shape[2],1)
return v
image = np.array([[[ 0.67826139, 0.29380381],
[ 0.90714982, 0.52835647],
[ 0.4215251 , 0.45017551]],
[[ 0.92814219, 0.96677647],
[ 0.85304703, 0.52351845],
[ 0.19981397, 0.27417313]],
[[ 0.60659855, 0.00533165],
[ 0.10820313, 0.49978937],
[ 0.34144279, 0.94630077]]])
print ("image2vector(image) = " + str(image2vector(image)))
# 行归一化
def normalizeRows(x):
x_norm = np.linalg.norm(x, ord = 2, axis = 1, keepdims = True)
# l2范数,axis=1沿着行,axis=0沿着列
x = x / x_norm
return x
def sofmax(x):
x_exp = np.exp(x)
x_sum = np.sum(x_exp, axis = 1, keepdims = True)
s = x_exp / x_sum # 在这里x是m*n,x_sum是m*1, size(m,n)/size(m,1),自动进行了broadcasting
return s
dot = np.dot(x1, x2) # 求内积
outer = np.outer(x1, x2) # x1' * x2
mul = np.multiply(x1, x2) # 逐像素相乘
dot = np.dot(W, x1) # size(3,1)与x1的内积的结果为size(1,3)
def L1(yhat, y):
loss = np.sum(np.abs(yhat - y))
return loss
def L2(yhat, y):
loss = np.dot(yhat - y, (yhat - y).T)
return loss
-
行归一化
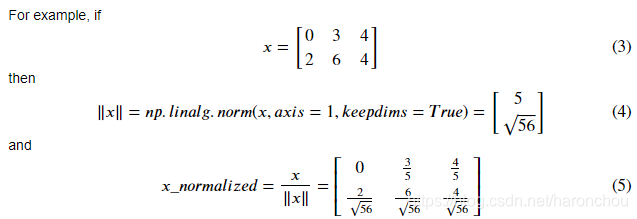
def normalizeRows(x):
x_norm = np.linalg.norm(x, ord = 2, axis = 1, keepdims = True)
# l2范数,axis=1沿着行,axis=0沿着列
x = x / x_norm # 自动复制补齐另外的维度
return x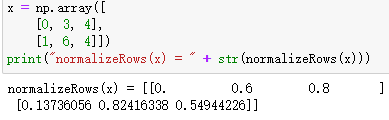
- numpy的Broadcasting和softmax函数
- numpy中的Broadcasting可以在不同size的数组之间进行数组运算。
- sofmax在多分类时会用到,其实就是归一化函数,即对数据的每一行进行归一化

def sofmax(x):
x_exp = np.exp(x)
x_sum = np.sum(x_exp, axis = 1, keepdims = True)
s = x_exp / x_sum # 在这里x是m*n,x_sum是m*1, size(m,n)/size(m,1),自动进行了broadcasting
return s
image2vector常用于深度学习 - np.reshape被广泛使用。将来,你会发现保持矩阵/矢量的维度直接将消除大量的错误。 - numpy具有高效的内置功能 - broadcasting非常有用
- 矢量化:dot,outer,elementwise product之间的区别
- dot是内积,就是求
,a,b均为行向量。
- outer是向量乘法,为
- elementwise就是逐像素相乘,点积
- dot是内积,就是求
dot = np.dot(x1, x2) # 求内积
outer = np.outer(x1, x2) # x1' * x2
mul = np.multiply(x1, x2) # 逐像素相乘
dot = np.dot(W, x1) # size(3,1)与x1的内积的结果为size(1,3)
- L1和L2代价函数的实现
def L1(yhat, y):
loss = np.sum(np.abs(yhat - y))
return loss
def L2(yhat, y):
loss = np.dot(yhat - y, (yhat - y).T)
return loss作业2:建立一个逻辑回归分类器识别猫
构建一个学习算法的总体架构,包括:
- 初始化参数
- 计算代价函数及其梯度
- 使用优化算法(梯度下降) 将上述三个函数按照正确的顺序集成到主模型函数中。
1 - Packages
首先,运行下面的单元格,导入您在此作业中需要的所有软件包。
- numpy 科学计算的基本软件包。
- h5py 是与数据集(存储在H5文件中的数据集)交互的常用软件包。
- matplotlib 著名的绘图工具
- PIL and scipy 最后环节用自己的图片测试自己的模型。
2 - Overview of the Problem set
给你一个数据集“data.h5",h5py是与数据集交互的常用软件包。数据集包含以下信息:
- - 训练集:带标签的数据,猫y=1和非猫y=0
- -测试集
- -每一幅图像都是64*64*3大小,且px=py
任务:构造一个简单的图像识别算法,可以正确的将图像分类为猫和非猫
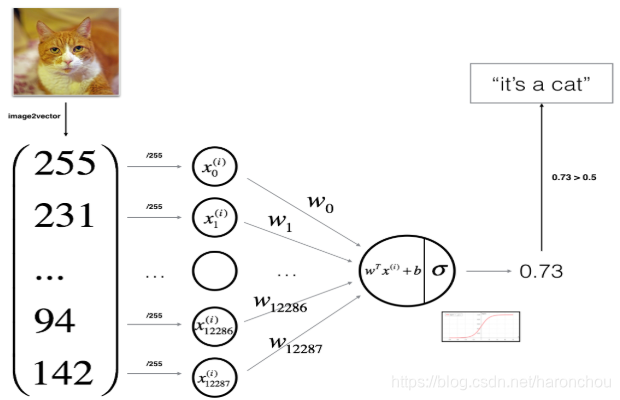
- (1)加载数据:全是array类型的数据,train.shape为(209,64,64,3),class为(2,),test.shape为(50,64,64,3),每一行为一个图像的数组。shape[0]=209,shape[1]=64,shaple[3]=3
#全是array类型的数据,train.shape为(209,64,64,3),class为(2,)
train_set_x_orig, train_set_y, test_set_x_orig, test_set_y, classes = load_dataset()- (2)数据预处理:全部reshape为X=(x1,x2,...,xm),每一列为一个样本
# 先拉成一列,reshape(train.shape[0],-1).T,就是全整成一行,剩下的程序自己算,所以是-1
train_set_x_flatten = train_set_x_orig.reshape(train_set_x_orig.shape[0],-1).T- (3)图像数据标准化:减去均值/标准差——标准化
- (4)建立逻辑回归实现猫的识别
- 初始化模型参数
- 通过最小化代价函数学习参数
- 使用学习到的参数在测试集上进行预测
- 对结果进行分析和总结
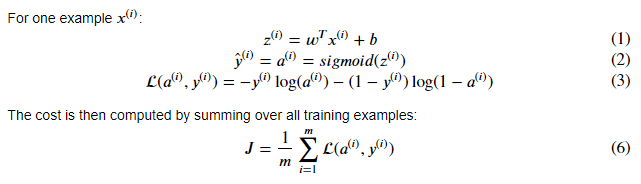


- (5)向前传播和向后传播
def sigmoid(z):
s = 1 / (1 + np.exp(-z))
return s
# 权重w初始化为零向量, w^T*x+b为模型
def initialize_with_zeros(dim):
w = np.zeros((dim,1)) #dim*1的列向量,对应于每一个Pixel输入
b = 0
return w,b
# 前向传播和反向传播
def propagate(w, b, X, Y):
m = X.shape[1] # 样本个数
A = sigmoid(np.dot(w.T, X) + b)
cost = -1 / m * np.sum( Y * np.log(A) + (1 - Y) * np.log(1 - A))
dw = np.dot(X, (A - Y).T) / m
db = np.sum(A - Y) / m
cost = np.squeeze(cost)
grads = {"dw":dw,
"db":db}
return grads, cost- (6)优化:梯度下降来更新参数
# 梯度下降更新参数
def optimize(w, b, X, Y, num_iterations, learning_rate, print_cost = False):
costs = []
for i in range(num_iterations):
grads, cost = propagate(w, b, X, Y)
dw = grads["dw"]
db = grads["db"]
# 梯度下降更新
w = w - learning_rate * dw
b = b - learning_rate * db
if i % 100 == 0 :
costs.append(cost)
if print_cost and i % 100 == 0:# 每隔100此打印代价函数
print("第%i此迭代后的cost:%f" %(i, cost))
params = {"w":w,
"b":b}
grads = {"dw":dw,
"db":db}
return params, grads,costs- (7)预测:用训练好的参数进行预测 𝑌̂ =𝐴=𝜎(𝑤𝑇𝑋+𝑏)
# 使用训练好的参数进行预测
def predict(w, b, X):
m = X.shape[1]
Y_prediction = np.zeros((1,m))
w = w.reshape(X.shape[0], 1)
A = sigmoid(np.dot(w.T, X) + b)
Y_prediction[A <= 0.5] = 0
Y_prediction[A > 0.5] = 1
assert(Y_prediction.shape == (1, m))
return Y_prediction - (8)合并整个模型
def model(X_train, Y_train, X_test, Y_test, num_iterations = 2000, learning_rate = 0.5, print_cost = False):
# 参数初始化
w, b = initialize_with_zeros(X_train.shape[0]) # 有多少特征
# 计算出最优化参数
parameters, grads, costs = optimize(w, b, X_train, Y_train, num_iterations, learning_rate)
w = parameters["w"]
b = parameters["b"]
# 对训练集和测试集进行预测
Y_prediction_test = predict(w, b, X_test)
Y_prediction_train = predict(w, b, X_train)
print("train accuracy: {} %".format(100 - np.mean(np.abs(Y_prediction_train - Y_train)) * 100))
print("test accuracy: {} %".format(100 - np.mean(np.abs(Y_prediction_test - Y_test)) * 100))
d = {"costs": costs,
"Y_prediction_test": Y_prediction_test,
"Y_prediction_train" : Y_prediction_train,
"w" : w,
"b" : b,
"learning_rate" : learning_rate,
"num_iterations": num_iterations}
return dComment: 训练的准确性接近100%。This is a good sanity check: 您的模型正在运行,并且具有足够的能力来拟合训练数据。测试错误是70%。考虑到我们使用的数据集较小,而且逻辑回归是一个线性分类器,所以对于这个简单的模型这个结果实际上并不差。不用担心,下周会建立一个更好的分类器!
另外,您会发现模型明显过拟合。稍后你将学习如何防止过拟合,例如通过正则化。使用下面的代码(更改index变量),您可以查看测试集的图片预测。
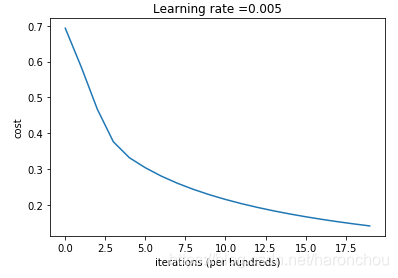
您会看到每次迭代,代价函数都在下降。表明正在学习参数。 但是,您看到可以在训练集上训练更多模型。 尝试增加迭代次数,然后重新运行。 您可能会看到训练集准确性提高了,但是测试集准确性却降低了。 这称为过度拟合。
- (9)进一步分析
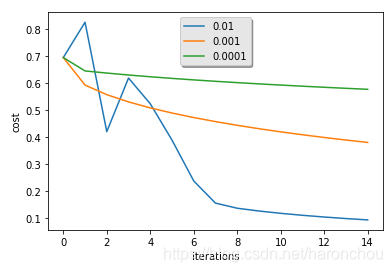
- 选择学习率α:决定了更新参数的速度,α太大则跳过最优解,α太小则收敛太慢。

























 926
926

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








