二叉树基础详解和Python代码定义，各种二叉树遍历方式详解和Python实现

二叉树基础详解

二叉树的种类

满二叉树

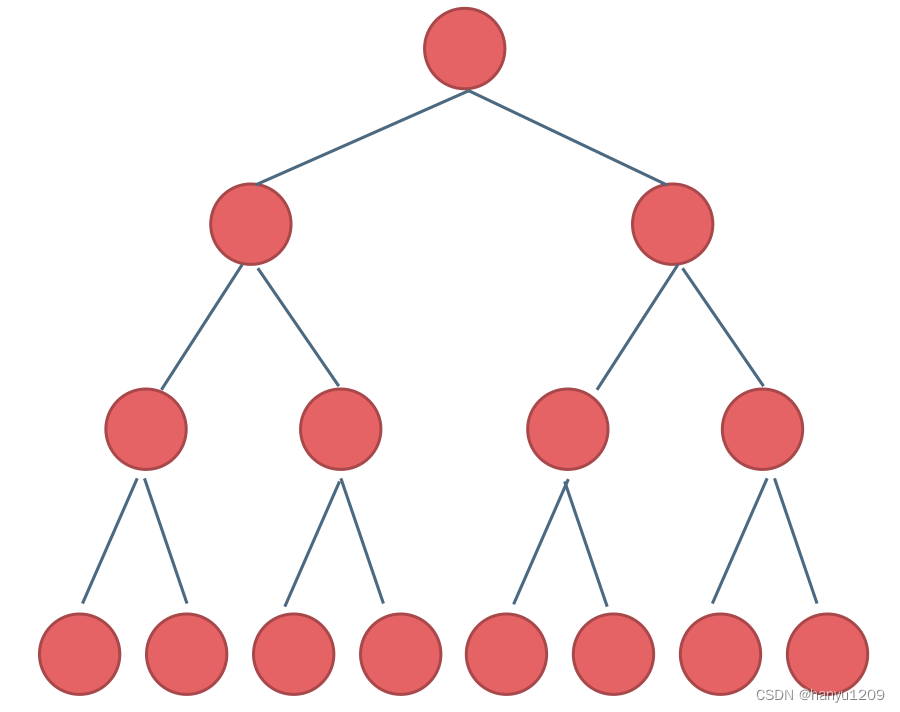
满二叉树：如果一棵二叉树只有度为0的结点和度为2的结点，并且度为0的结点在同一层上，则这棵二叉树为满二叉树。

完全二叉树

完全二叉树的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2^(h-1) 个节点。

二叉搜索树

前面介绍的树，都没有数值的，而二叉搜索树是有数值的了，二叉搜索树是一个有序树。

●若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
●若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
●它的左、右子树也分别为二叉排序树

平衡搜索二叉树

平衡二叉搜索树：又被称为AVL（Adelson-Velsky and Landis）树，且具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。

二叉树的储存方式

二叉树可以链式存储，也可以顺序存储。
但我们一般都用链式储存

那么链式存储方式就用指针， 顺序存储的方式就是用数组。

顾名思义就是顺序存储的元素在内存是连续分布的，而链式存储则是通过指针把分布在各个地址的节点串联一起。

二叉树的遍历方式

二叉树主要有两种遍历方式：

深度优先遍历：先往深走，遇到叶子节点再往回走。
广度优先遍历：一层一层的去遍历。
这两种遍历是图论中最基本的两种遍历方式，后面在介绍图论的时候 还会介绍到。

那么从深度优先遍历和广度优先遍历进一步拓展，才有如下遍历方式：

深度优先遍历
●前序遍历（递归法，迭代法）
●中序遍历（递归法，迭代法）
●后序遍历（递归法，迭代法）
广度优先遍历
层次遍历（迭代法）
在深度优先遍历中：有三个顺序，前中后序遍历， 有同学总分不清这三个顺序，经常搞混，我这里教大家一个技巧。

这里前中后，其实指的就是中间节点的遍历顺序，只要大家记住 前中后序指的就是中间节点的位置就可以了。

看如下中间节点的顺序，就可以发现，中间节点的顺序就是所谓的遍历方式

●前序遍历：中左右
●中序遍历：左中右
●后序遍历：左右中
大家可以对着如下图，看看自己理解的前后中序有没有问题。

最后再说一说二叉树中深度优先和广度优先遍历实现方式，我们做二叉树相关题目，经常会使用递归的方式来实现深度优先遍历，也就是实现前中后序遍历，使用递归是比较方便的。

二叉树的定义（Python）

class TreeNode:
    def __init__(self, value):
        self.value = value
        self.left = None
        self.right = None

二叉树的深度优先遍历（递归）：

前序遍历（中左右）

力扣144. 二叉树的前序遍历

class Solution:
    def preorderTraversal(self, root: Optional[TreeNode])-> List[int]:
        result = []                       #保存结果
        def transfer(root):
            if root==None:
                return
            result.append(root.val)        #前序
            transfer(root.left)            #左
            transfer(root.right)           #右
        transfer(root)
        return result

中序遍历&