链表题目汇总：逆置，合并，分割，返回特定结点，回文，环形

链表常见oj题目解法

链表反转

常见思路：将各节点取出，依次头插，返回新链表

如图所示，注意链表的尾结点指针域置空

struct ListNode* reverseList(struct ListNode* head){
    struct ListNode*rhead=NULL;
    struct ListNode*cur=head;
    while(cur){
        struct ListNode*pre=cur->next;
        cur->next=rhead;
        rhead=cur;
        cur=pre;
    }return rhead;
    
}

链表合并

要求：将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。

常见思路：
两个指针，分别指向待合并的两个链表，比较指向的节点的大小，取小的尾插到返回链表中。当两个链表的指针一个为空时，合并完成，将不为空的那个链表链接到返回链表即可。
为了便于维护，我们设置头节点在返回链表中。**但结束时要注意释放！**合并过程如图所示：

struct ListNode* mergeTwoLists(struct ListNode* list1, struct ListNode* list2)
{
	struct ListNode* head=(struct ListNode*)malloc(sizeof(struct ListNode));
	struct ListNode*tail=head;
	tail->next=NULL;
	while(list1 && list2)
	{
		if(list1->val <list2->val)
		{
			tail->next=list1;
			list1=list1->next;
			tail=tail->next;
		}else
		{
			tail->next=list1;
			list1=list1->next;
			tail=tail->next;
		}
	}if(list1)
	{
		tail->next=list2;
	}if(list2)
	{
		tail->next=list1;
	}
	struct ListNode*newhead=head->next;
	free(head)
	return newhead;
}

链表的分割

要求：以给定值x为基准将链表分割成两部分，所有小于x的结点排在大于或等于x的结点之前
常见思路：创建两个链表，分别存放小于x的节点和大于等于x的节点，分别进行尾插，最后链接起来。注意，链表的尾部节点要置空NULL

ListNode* partition(ListNode* pHead, int x) {
	ListNode*head1,*tail1,*head2,*tail2;
	head1=( ListNode*)malloc(sizeof( ListNode));
    head2=( ListNode*)malloc(sizeof( ListNode));
    tail1=head1;
    tail2=head2;
    head1->next=head2->next=NULL;
    while(pHead)
    {
    	if(pHead->val <x)
    	{
    		tail1->next=pHead;
    		tail1=tail1->next;
    		pHead=pHead->next;
    	}else
    	{
    		tail2->next=pHead;
    		tail2=tail2->next;
    		pHead=pHead->next;
    	}
    }
    //两个链表链接
    tail1->next=head2->next;
    //尾结点置空，防止成环
    tail2->next=NULL;
    //释放两个自己创建的头结点
    ListNode*newHead=head1->next;
    free(head1);
    free(head2);
    return newHead;
}

返回链表的倒数第k个节点

常见思路：快慢指针，慢指针从头出发，快指针先走K步，然后同时出发，一次移动一步，直到快指针指向NULL，慢指针指向的即为第k个节点。

示例：返回倒数第2个节点


以此类推，列出结束时情况

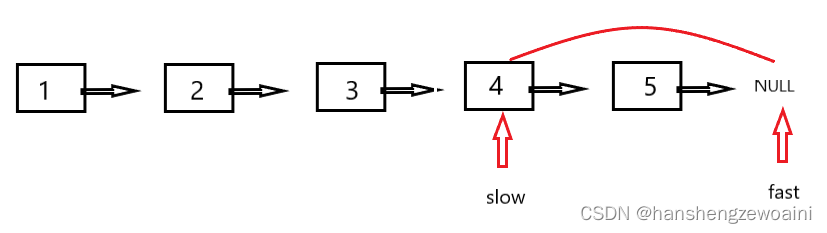
此时slow指向的是倒数第2个节点

struct ListNode* FindKthToTail(struct ListNode* pListHead, int k ) {
    if (!pListHead || k <= 0) //链表为空或k<0
    {
    	return NULL;
    }
    struct ListNode* slow, * fast;
    fast = slow = pListHead;
    while (k--)
    {
        if (fast)
        {
            fast = fast->next;
        }
        else //  k>链表长度
        {
            return NULL;
        }
    }
    while (fast)
    {
        slow = slow->next;
        fast = fast->next;
    }return slow;
}

回文链表判定

要求：对于一个链表，请设计一个时间复杂度为O(n),额外空间复杂度为O(1)的算法，判断其是否为回文结构。
1->2->2->1 ture
1->2->3->1 false
1->2->3->2->1 true

常见解法：

1. 找到链表中间节点
2. 反转中间节点后半部分的链表
3. 两段链表比较，其中一个到NULL后停止

class PalindromeList {
public:
    bool chkPalindrome(ListNode* A) {
    //返回中间节点
    ListNode* head=(ListNode* )malloc(sizeof(ListNode));
    ListNode* slow,*fast;
    head->next=A;
    slow=fast=head;
    while(fast && fast->next)
    {
    	slow=slow->next;
    	fast=fast->next->next;
    }
    //倒置链表
    ListNode*cur=slow->next;
    ListNode*rhead=NULL;
    slow->next=NULL; //分割，防止成环
    while(cur)
    {
    	ListNode*next=cur->next;
    	cur->next=rhead;
    	rhead=cur;
    	cur=next;
    }
    //两边分别遍历
    while(rhead && A){
            if(rhead->val!=A->val){
                return false;
            }
            rhead = rhead->next;
            A = A->next;
        }
        return true;
    }
 }

环形链表

判定链表中是否有环

判定方法：快慢指针，同时出发，快指针每次走两步，慢指针每次走一步，如果快指针能够追上慢指针，即fastslow时，说明链表有环。否则，当fastNULL 或fast->next==NULL 时，证明无环。

bool hasCycle(struct ListNode *head) {
   Node* slow = head;
   Node* fast = head;
 
  while(fast && fast->next)
  {
    slow = slow->next;
    fast = fast->next->next;
 
    if(slow == fast)
      return true;
  }
 
  return false;
}

找到链表中成环的节点

常见方法：
1.判断是否有环，有的话找到slow和fast的相遇点
2.链表首结点处设置指针，与slow同时走一步，直到两者相遇即为链表成环节点

证明：
fast一次走两步，slow一次走一步，fast的速度是slow的两倍，故相同起点出发，经过相同时间，fast的路程也是slow的两倍。如果链表存在环，则fast与slow一定会相遇。
设链表头到成环入口处相距L，环的距离是C，则相遇时遇点到环入口点的距离为X：
slow的路程：L+X
fast的路程：L+X+N*C (N代表走过环的圈数，不排除环很小，L很大的情况，会使得相遇时fast走过多圈)

所以，可以列出等式 （L+X）*2=（L+X+NC）
L+X=2NC=KC（K为常数）
我们想求环入口点， L=KC-X
所以从相遇点开始slow继续走，让一个指针从头开始走，相遇点即为入口节点

typedef struct ListNode Node;
struct ListNode *detectCycle(struct ListNode *head) {
    	Node* slow = head;
        Node* fast = head;
 
        while(fast && fast->next)
        {
            slow = slow->next;
            fast = fast->next->next;
            //走到相遇点
            if(slow == fast)
            {
                // 求环的入口点
                Node* meet = slow;
                Node* start = head;
 
                while(meet != start)
                {
                    meet = meet->next;
                    start = start->next;
                }
 
                return meet;
            }
        }
 
        return NULL;
}