Kmean算法
聚类算法
对于"监督学习"(supervised learning),其训练样本是带有标记信息的,并且监督学习的目的是:对带有标记的数据集进行模型学习,从而便于对新的样本进行分类。而在“无监督学习”(unsupervised learning)中,训练样本的标记信息是未知的,目标是通过对无标记训练样本的学习来揭示数据的内在性质及规律,为进一步的数据分析提供基础。对于无监督学习,应用最广的便是"聚类"(clustering)。
“聚类算法”试图将数据集中的样本划分为若干个通常是不相交的子集,每个子集称为一个“簇”(cluster),通过这样的划分,每个簇可能对应于一些潜在的概念或类别。
kmeans算法又名k均值算法。其算法思想大致为:先从样本集中随机选取 k 个样本作为簇中心,并计算所有样本与这 k 个“簇中心”的距离,对于每一个样本,将其划分到与其距离最近的“簇中心”所在的簇中,对于新的簇计算各个簇的新的“簇中心”
算法的算法过程如下:
D为训练集,K为聚类簇的个数,maxIter最大迭代次数
KMeans(D, K, maxIter):
随机选取K个中心点
for j in range(m):
计算每个样本Xj到各个簇中心的距离
根据最近距离,筛选样本归属于哪个簇
for i in range(k):
计算新的簇的中心,利用均值
如果簇中心改变,则更新该簇中心,否则不变
如果每个簇的中心都没更新则退出算法算法分析:
kmeans算法由于初始“簇中心”点是随机选取的,因此最终求得的簇的划分与随机选取的“簇中心”有关,也就是说,可能会造成多种 k个簇的划分情况。这是因为kmeans算法收敛到了局部最小值,而非全局最小值。
二分k-means算法
基于kmeans算法容易使得结果为局部最小值而非全局最小值这一缺陷,对算法加以改进。使用一种用于度量聚类效果的指标SSE(Sum of Squared Error),即对于第 ii 个簇,其SSE为各个样本点到“簇中心”点的距离的平方的和,SSE值越小表示数据点越接近于它们的“簇中心”点,聚类效果也就越好。以此作为划分簇的标准。
算法思想是:先将整个样本集作为一个簇,该“簇中心”点向量为所有样本点的均值,计算此时的SSE。若此时簇个数小于 k,对每一个簇进行kmeans聚类(k=2) ,计算将每一个簇一分为二后的总误差SSE,选择SSE最小的那个簇进行划分操作。
算法的算法过程如下:
D为训练集,K为聚类簇的个数,maxIter最大迭代次数
KMeans(D, K, maxIter):
将所有点看做一个簇,计算此时“簇中心”向量
while “簇中心”个数h<k :
for i=1,2,...,h do
将第 i 个簇使用 kmeans算法进行划分,其中 k=2
计算划分后的误差平方和 SSEi
比较 k 种划分的SSE值,选择SSE值最小的那种簇划分进行划分
更新簇的分配结果
添加新的“簇中心”
until 当前“簇中心”个数达到 k二分k-means算法分析:
二分k-means算法不再随机选取簇中心,而是从一个簇出发,根据聚类效果度量指标SSE来判断下一步应该对哪一个簇进行划分,因此该方法不会收敛到局部最小值,而是收敛到全局最小值。
HMM模型
隐马尔可夫模型(Hidden Markov Model,以下简称HMM)。
1、什么样的问题需要HMM模型
使用HMM模型的问题一般有一下两个特征:
1)问题是基于序列的,比如时间序列或者状态序列。
2)问题中有两类数据,一列序列数据是可以观测的,即观测序列;而另一类数据是不能观测到的,即隐藏状态序列,简称状态序列。
有这两个特征,那么问题一般可以用HMM模型解决。这样的问题在实际生活中是很多的。比如:打字的过程,在键盘上敲出来的一系列字符就是观测序列,而实际想输入的句子就是隐藏序列,输入法的任务就是根据敲入的一系列字符尽可能的猜测我要输入的词语,并把最可能的词语放在最前面,这就可以看做一个HMM模型。
2、HMM模型的定义
HMM模型详细介绍:http://www.52nlp.cn/hmm-learn-best-practices-two-generating-patterns
http://www.52nlp.cn/hmm-learn-best-practices-three-hidden-patterns
http://www.52nlp.cn/hmm-learn-best-practices-four-hidden-markov-models
对于HMM模型,假设Q是所有可能的隐藏状态的集合,V是所有可能的观测状态的集合,即:
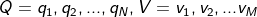
其中,N是可能的隐藏状态数,M是所有的可能的观察状态数。
对于一个长度为T的序列,I对应的状态序列, O是对应的观察序列,即:
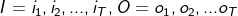
其中,任意一个隐藏状态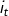 ∈Q, 任意一个观察状态
∈Q, 任意一个观察状态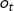 ∈V。
∈V。
HMM模型做了两个很重要的假设如下:
1)齐次马尔科夫链假设。即任意时刻的隐藏状态只依赖于它前一个隐藏状态。当然这样假设有点极端,因为很多时候我们的某一个隐藏状态不仅仅只依赖于前一个隐藏状态,可能是前两个或者是前三个。但是这样假设的好处就是模型简单,便于求解。如果在时刻t的隐藏状态是,在时刻t+1的隐藏状态是
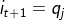 , 则从时刻t到时刻t+1的HMM状态转移概率
, 则从时刻t到时刻t+1的HMM状态转移概率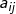 可以表示为:
可以表示为:
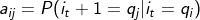
这样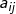 可以组成马尔科夫链的状态转移矩阵A:
可以组成马尔科夫链的状态转移矩阵A:
![A=[a_i_j]_N_*_N](https://i-blog.csdnimg.cn/blog_migrate/ebb2c8de29fd839c2994462aadfa83e9.gif)
2)观测独立性假设。即任意时刻的观察状态只仅仅依赖于当前时刻的隐藏状态,这也是一个为了简化模型的假设。如果在时刻t的隐藏状态是, 而对应的观察状态为
, 则该时刻观察状态
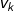 在隐藏状态
在隐藏状态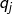 下生成的概率为
下生成的概率为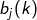 ,满足:
,满足:
这样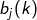 可以组成观测状态生成的概率矩阵B:
可以组成观测状态生成的概率矩阵B:
![B=[b_j(k)]_N_*_M](https://i-blog.csdnimg.cn/blog_migrate/6ab8e073d60b110f8de43bc0fe88a20a.gif)
除此之外,我们需要一组在时刻t=1的隐藏状态概率分布Π:
![\Pi =[\pi(i)]_N](https://i-blog.csdnimg.cn/blog_migrate/34c7927873065cefd0e53ecf5685d8e0.gif) , 其中
, 其中 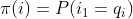
一个HMM模型,可以由隐藏状态初始概率分布Π, 状态转移概率矩阵A和观测状态概率矩阵B决定。Π, A决定状态序列,B决定观测序列。因此,HMM模型可以由一个三元组λ表示如下:
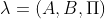
3、一个HMM模型实例
一个简单的实例来描述上面抽象出的HMM模型。这是一个盒子与球的模型,例子来源于李航的《统计学习方法》。
假设我们有3个盒子,每个盒子里都有红色和白色两种球,这三个盒子里球的数量分别是:

按照下面的方法从盒子里抽球,开始的时候,从第一个盒子抽球的概率是0.2,从第二个盒子抽球的概率是0.4,从第三个盒子抽球的概率是0.4。以这个概率抽一次球后,将球放回。然后从当前盒子转移到下一个盒子进行抽球。规则是:如果当前抽球的盒子是第一个盒子,则以0.5的概率仍然留在第一个盒子继续抽球,以0.2的概率去第二个盒子抽球,以0.3的概率去第三个盒子抽球。如果当前抽球的盒子是第二个盒子,则以0.5的概率仍然留在第二个盒子继续抽球,以0.3的概率去第一个盒子抽球,以0.2的概率去第三个盒子抽球。如果当前抽球的盒子是第三个盒子,则以0.5的概率仍然留在第三个盒子继续抽球,以0.2的概率去第一个盒子抽球,以0.3的概率去第二个盒子抽球。如此下去,直到重复三次,得到一个球的颜色的观测序列:
O={红,白,红}.
注意在这个过程中,观察者只能看到球的颜色序列,却不能看到球是从哪个盒子里取出的。
那么按照我们上一节HMM模型的定义,我们的观察集合是:
V={红,白},M=2
我们的状态集合是:
Q={盒子1,盒子2,盒子3},N=3
而观察序列和状态序列的长度为3.
初始状态分布为:
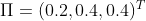
状态转移概率分布矩阵为:
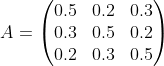
观测状态概率矩阵为:
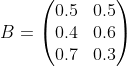
从上一节的例子,可以抽象出HMM观测序列生成的过程。
输入的是HMM的模型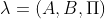 ,观测序列的长度T
,观测序列的长度T
输出是观测序列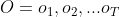
生成的过程如下:
1)根据初始状态概率分布Π生成隐藏状态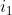
2) for t from 1 to T
a. 按照隐藏状态it的观测状态分布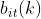 生成观察状态
生成观察状态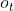 .
.
b. 按照隐藏状态it的状态转移概率分布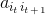 产生隐藏状态
产生隐藏状态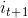 .
.
所有的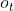 一起形成观测序列
一起形成观测序列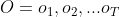
HMM模型一共有三个经典的问题需要解决:
1) 评估观察序列概率。即给定模型λ=(A,B,Π)和观测序列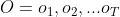 ,计算在模型λ下观测序列O出现的概率P(O|λ)。这个问题的求解需要用到前向后向算法。
,计算在模型λ下观测序列O出现的概率P(O|λ)。这个问题的求解需要用到前向后向算法。
2)模型参数学习问题。即给定观测序列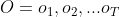 ,估计模型λ=(A,B,Π)的参数,使该模型下观测序列的条件概率P(O|λ)最大。这个问题的求解需要用到基于EM算法的Baun-Welch算法。这个问题是HMM模型三个问题中最复杂的。
,估计模型λ=(A,B,Π)的参数,使该模型下观测序列的条件概率P(O|λ)最大。这个问题的求解需要用到基于EM算法的Baun-Welch算法。这个问题是HMM模型三个问题中最复杂的。
3)预测问题,也称为解码问题。即给定模型λ=(A,B,Π)和观测序列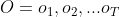 ,求给定观测序列条件下,最可能出现的对应的状态序列,这个问题的求解需要用到基于动态规划的维特比(Viterbi)算法。这个问题是HMM模型三个问题中复杂度居中的算法。
,求给定观测序列条件下,最可能出现的对应的状态序列,这个问题的求解需要用到基于动态规划的维特比(Viterbi)算法。这个问题是HMM模型三个问题中复杂度居中的算法。
Baun-Welch算法,Viterbi解码算法将在下一篇学习日志中介绍。





 本文介绍了二分k-means算法和HMM模型。二分k-means算法是对kmeans算法的改进,可收敛到全局最小值。HMM模型适用于基于序列且有观测和隐藏状态序列的问题,文中给出其定义、实例,还提及该模型需解决评估观察序列概率、模型参数学习、预测三个经典问题。
本文介绍了二分k-means算法和HMM模型。二分k-means算法是对kmeans算法的改进,可收敛到全局最小值。HMM模型适用于基于序列且有观测和隐藏状态序列的问题,文中给出其定义、实例,还提及该模型需解决评估观察序列概率、模型参数学习、预测三个经典问题。
















 6293
6293

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








