MATLAB画图（二）

三维曲线

 plot3函数

（1）plot3函数的基本用法

plot3(x, y, z)

其中，参数x、y、z组成一组曲线的坐标。

（2）plot3(x,y,z)函数参数的变化形式

plot3(X, Y, Z)

 参数X、Y、Z是同型矩阵时，以X、Y、Z对应列元素绘制曲线，曲线条数等于矩阵列数。

 参数X、Y、Z中有向量，也有矩阵时，向量的长度应与矩阵相符。

（3）含多组输入参数的plot3函数

plot3(x1, y1, z1, x2, y2, z2, …, xn, yn, zn)

每一组x、y、z向量构成一组数据点的坐标，绘制一条曲线。

（4）含选项的plot3函数

plot3(x, y, z, 选项)

选项用于指定曲线的线型、颜色和数据点标记。

 fplot3函数

fplot3(funx, funy, funz, tlims)

其中，funx、funy、funz代表定义曲线x、y、z坐标的函数，通常采用函数句柄的形式。tlims为参数函数自变量的取值范围，用二元向量[tmin, tmax]描述，默认为[-5, 5]。

例：

x=@(t) exp(-t/10).*sin(5*t)
y=@(t) exp(-t/10).*cos(5*t)
z=@(t) t
fplot3(x,y,z,[-12,12])

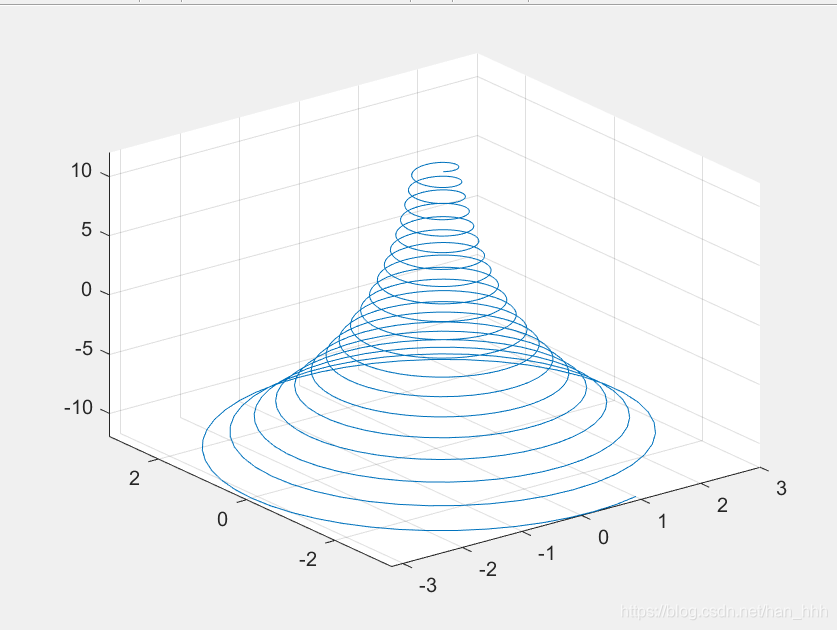
在fplot3函数中，可以指定曲线的线型、颜色或数据点标记。

fplot3(xt, yt, zt, [-12, 12], 'r-.')

三维曲面

1．平面网格数据的生成

在MATLAB中，产生平面区域内的网格坐标矩阵有两种方法。

(1)利用矩阵运算生成。

>> x = 2:6;

>> y = (3:8)';

>> X = ones(size(y))*x;

>> Y = y*ones(size(x));

X和Y相同位置上的元素，如X32、Y32是区域的第3行第2列网格点的坐标(3,5)。

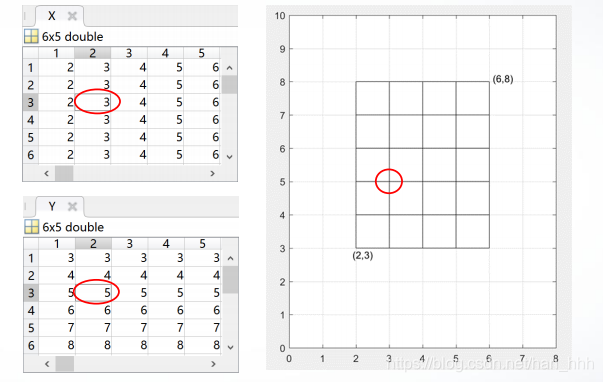
(2)利用meshgrid函数生成。

[X,Y]=meshgrid(x,y);

其中，参数x、y为向量，存储网格点坐标的X、Y为矩阵。

>> x = 2:1:6;

>> y = (3:1:8)';

>> [X, Y] = meshgrid(x, y);

第3行命令生成的网格坐标矩阵X、Y与方法(1)得到的相同。

2．绘制三维曲面的函数

 mesh函数和surf函数的调用格式：

mesh(x, y, z, c)   线条有颜色，线条间补面无颜色

surf(x, y, z, c)     线条和线条间补面都有颜色

其中，x、y是网格坐标矩阵，z是网格点上的高度矩阵，c用于指定在不同高度下的曲面颜色。c省略时，颜色的设定正比于图形 的高度。

 mesh函数和surf函数的其他调用格式：

mesh(z, c)

surf(z, c)

当x、y省略时，z矩阵的第2维下标当作x轴坐标，z矩阵的第1维下标当作y轴坐标。

 带等高线的三维网格曲面函数meshc

 带底座的三维网格曲面函数meshz

 具有等高线的曲面函数surfc

 具有光照效果的曲面函数surfl

 

3. 标准三维曲面

（1）sphere函数

[x,y,z]=sphere(n)

产生3个(n+1)阶的方阵，采用这3个矩阵可以绘制出圆心位于原点、半径为1的单位球体。

（2）cylinder函数

[x,y,z]=cylinder(R, n)

其中，参数R是一个向量，存放柱面各个等间隔高度上的半径，n表示在圆柱圆周上有n个间隔点，默认有20个间隔点。

 

（3）peaks 函数

peaks函数的调用格式：

peaks(n)                                  >> p1=peaks(10);

peaks(V)                                  >> p2=peaks;

peaks(x,y)                                >> p3=peaks(-3:0.2:3);

                                                  >> [x,y]=meshgrid(-2:0.1:2, 0:0.1:5);

peaks                                        >> p4=peaks(x,y);

4．fmesh函数和fsurf函数

用于绘制参数方程定义的曲面

fsurf(funx, funy, funz, uvlims)

fmesh(funx, funy, funz, uvlims)

其中，funx、funy、funz代表定义曲面x、y、z坐标的函数，通常采用函数句柄的形式。uvlims为funx、funy和funz的自变量的取值范围，用4元向量[umin, umax, vmin, vmax]描述 ，默认为[-5, 5, -5, 5]。