Psi‐演算工作台：通用进程分析工具

Psi‐演算工作台：一种用于应用进程演算的通用工具

¨ ¯约翰内斯·博格斯特伦，拉穆纳斯·古特科瓦斯，伊奥安娜·罗德赫¨和比约恩·维克托，乌普萨拉大学

ψ‐演算是一种参数化框架，用于扩展π‐演算以支持任意数据和逻辑。该框架的所有实例均继承了经过机器检查的 元理论证明，例如组合性和双模拟同余。我们提出了一种面向ψ‐演算实例的通用分析工具，支持对单播和广播通 信进行符号执行以及（双）模拟验证。该工具还提供了一个用于实现新ψ‐演算实例的库。我们给出了来自传统通 信协议和无线传感器网络的示例。我们还描述了该工具的理论基础，包括一种改进的符号操作语义，新增了对作 用域广播通信的支持。

分类与主题描述：C.2.2[Computer-Communication Networks]：网络协议—协议验证；D.2.2[Software Engineering]：设计工具与技术；I.1.4[Symbolic andAlgebraic Manipulation]：应用 通用术语：设计、理论、验证 附加关键词与短语：无线传感器网络，进程演算，符号语义

ACM引用格式
约翰内斯·博格斯特伦、拉穆纳斯·古特科瓦斯、伊奥安娜·罗德赫和比约恩·维克托。2015年。Psi‐演算工作台：一 种用于应用进程演算的通用工具。ACM嵌入式计算系统汇刊，第14卷，第1期，文章9（2015年1月），25页。
DOI: http://dx.doi.org/10.1145/2682570

1. 引言

并发系统的开发得益于使用精确且形式化的系统模型。针对并发系统存在许多不同的形式 化方法，这些方法通常针对特定应用领域进行了专门化设计。对于每种形式化方法而言， 都需要相应的工具支持，以便构建和分析非平凡系统的模型。本文介绍了针对具有移动性 的进程演算通用语义框架的工具支持。因此，我们并非为每一种单独的进程演算分别开发 工具，而是为一整类进程演算开发一个统一的通用工具。

ψ‐演算 [Bengtson 等人 2011]是一种基于 π‐演算 [Milner 等人 1992a],的参数化 语义框架，能够针对每个应用程序定制数据语言和逻辑。该框架提供了多种特性，例如资 源的词法作用域局部名字、作为数据的通信通道、单播和广播通信 [Borgstr¨om 等人 2011], ，以及一阶和高阶通信 [Parrow 等人 2013]。

本工作由ProFun项目资助。作者地址：瑞典乌普萨拉，乌普萨拉大学，信息技术系，邮政信箱337，75105；电 子邮件：{johannes. borgstrom, ramunas.gutkovas, bjorn.victor}@it.uu.se, ioana.rodhe@foi.se。允许 出于个人或课堂教学目的，在不收取费用的情况下制作本作品全部或部分内容的数字版或纸质副本，但前提是不 得以盈利或商业利益为目的制作或分发这些副本，且每份副本必须在首页或显示设备的初始屏幕显著位置附上完 整的引用信息及本版权声明。对于本作品中由非ACM方拥有版权的组成部分，必须尊重其原有版权。允许在注明 出处的前提下进行摘要引用。如需其他用途，例如复制、重新发布、上传至服务器、向列表分发，或在其他作品 中使用本作品的任何组成部分，则必须事先获得特定许可和/或支付费用。许可申请可发送至：美国纽约彭广场2 号701室，邮编10121‐0701，ACM公司出版部，传真 +1(212) 869‐0481，或 permissions@acm.org。c © 2015 ACM 1539‐9087/2015/01‐ART9 $15.00 DOI: http://dx.doi.org/10.1145/2682570
ACM嵌入式计算系统汇刊，第14卷，第1期，文章9，出版日期：2015年1月。
nstory.ai 的开源 PDF 翻译库 BabelDOC v0.5.10 (http://yadt.io) 翻译，本仓库正在积极的建设当中，欢迎 star 和关注。

9:2 J. Borgstr¨om 等

π‐演算的许多不同扩展，包括spi‐演算[Abadi和Gordon 1997],、融合演算[Wischik和Gardner 2005],、并发约束pi‐演算[Buscemi和Montanari 2007],以及多 维同步pi‐演算[Carbone和Maffeis 2003],，都可以直接表示为ψ‐演算框架的实例。一个 主要优势是，所有元理论结果（包括bisimilarity的代数定律和同余性质）都适用于该框 架的任何有效实例。此外，其中大多数结果已经使用名义Isabelle定理证明器[Urban和 Tasson 2005]得到了严格证明。ψ‐演算的这些特性为使用者节省了大量工作——ψ‐演算是 一个可重用的框架。

本文介绍了Psi‐演算工作台（PWB），这是一个用于实现ψ‐演算实例以及分析相应实 例中进程的通用工具。尽管已有多种专门针对特定进程演算和应用领域的工具，我们的工 具具有通用性和可重用性。相比以往的工作，其适用范围更广，并且能够以相对较低的成 本对新的进程演算进行实验。与ψ‐演算类似，我们的工具是参数化的：它为任意估算演算 实例中的进程提供双模拟等价性检查和符号模拟（或执行）功能，以及一个用于实现新 ψ‐演算实例的基础库。因此，PWB有两类用户：一类是在框架的现有实例中分析系统的用 户，另一类是实例实现者。

我们通过三个步骤说明该工具的两种用途：在第2节中，我们半形式化地介绍ψ‐演算的 框架，关联对应于π‐演算的一个实例，并展示智能体的符号模拟。在第3节描述PWB的设 计以及如何实现一个实例之后，我们在第4节中通过建模用于可靠通信的传统交替比特协议 来展示如何添加数据和计算。在第5节中，我们为无线传感器网络建模一个数据聚合协议， 其中包含专用的数据结构和逻辑，以及单播和广播通信。第6节将前述示例扩展到动态拓扑。 在第7节中，我们描述了在PWB中实现的符号语义。第7.1节的符号操作语义简化了先前ψ‐ 演算的符号语义[Johansson et al. 2012]，并添加了用于无线（同步且不可靠）广播的规则[Borgstr¨om et al. 2011]。据我们所知，这是首个用于词法作用域广播通信的符号语义。 在第8节中，我们讨论相关工作。本文的简略版本已作为Borgstr¨om et al.[2013]发表。

2. 引入ψ‐演算

本节中，我们半形式化地介绍ψ‐演算参数化语义框架，并将一些精确定义和操作语义推迟 到第7节。关于ψ‐演算更详尽的论述，包括其需求动机和其他实例示例，参见Bengtson et al.[2011], Borgstr¨om et al. [2011],和Johansson et al. [2010, 2012]。我们在第4、 5和6节中展示更复杂的示例。

一个估算演算实例由三种数据类型指定：（数据）项T，以M,N表示；条件C，以 ϕ表 示；以及断言A，以 表示。这些项、条件和断言可以是任意集合，其中的元素可能包含 名字（来自名字集合 N），并允许名字置换（即所谓的名义集合[Pitts 2003]）。特别地， 每个元素X都有一个自由名称的有限集n(X) ⊆N，我们用a#X表示a ∈ n(X)。

ACM嵌入式计算系统汇刊，第14卷，第1期，文章9，出版日期：2015年1月。

Psi‐演算工作台 9:3

项既用作通信通道，也用作通信中发送和被接收的数据。项可以是结构化的，因此允 许使用标准结构如列表和集合、数字、布尔值，以及更复杂的结构。断言用于对项及其之 间的关系建模“事实”，例如通过为变量赋值或约束其取值范围。最小的断言是单位元， 记作1，断言通过 ⊗操作符进行组合。条件用于对项执行测试。其结果取决于当前的断言 环境，通过蕴含关系（ 蕴含 ϕ，记作 ϕ）确定，该蕴含关系也是psi实例规范的一 部分。

在Pi实例中，对应于多通道pi‐演算，项仅仅是名字a, b, c…，而条件是关于名字的相 等性测试。（名字相等性用于匹配结构[a= b]P，当且仅当a= b成立时，其行为与P 相同。）在π‐演算中没有断言，但ψ‐演算框架至少需要平凡单位断言。后续示例将展示如 何利用断言来建模高级特性。

给定psi‐演算参数T, C,A，智能体（用P, Q…表示）具有以下形式： ˜MN.P输出前缀M(˜x).P输入前缀˜M!N. P广播输出前缀M?(˜x).P广播输入前缀caseϕ1: P1[] ···[] ϕn:Pn选择(νa)P限制P | Q并行!P复制 ( ||)断言˜A〈M〉 调用

我们用M表示元组M1,… Mn。输出和输入前缀表示多播（单播）输出和输入，而广播 前缀表示（同步的）广播输出和输入，这种传输在无线系统中是不可靠的，即传输可能未 被接收。情况结构可以表现为任意满足相应条件ϕi为真的Pi；其他情况则被丢弃。限制将 a在P中进行绑定，输入前缀将 ˜x在其后缀中绑定；我们视α‐等价进程为相同。调用形式 用于调用由形式A(˜y)⇐P定义的进程A；其行为等同于˜P{M/ ˜y}。

在Pi实例中，输出和输入前缀是通常的a ˜x.P和a(˜x).P；匹配结构[a= b]P对 应于选择真:P。如果我们有一个恒为真的条件，就可以将非确定性选择（传统上写作P + Q）建模为选择恒真条件:P[]恒真条件:Q。

ψ‐演算的语义由标注转移关系定义，记作 P →α P′，表示在环境 中，代理 P 可以执行一个动作 α 迁移为P′。在π‐演算实例中，环境 始终是平凡的1，但一般 情况下，它表示环境的断言，包括并行代理。

语义仅对良构代理定义。代理中子项的出现称为受保护，如果它是前缀形式的一个真 子项。一个代理是结构良好的，当在M(˜x).P和M?(˜x).P中， ˜x是一个无重复元素的序 列；在选择ϕ1: P1[] ···[] ϕn: Pn中，代理Pi不包含无保护断言；且在复制!P中，代理P 不包含无保护断言或广播输入前缀。对于进程定义，适用与复制类似的条件。

9:4 J. Borgstr¨om 等人

动作包括输入M(˜x)，表示通过由M表示的˜ ˜通道接收 绑定到 ˜x的数据，以及输出M(ν ˜x)N，表示通过M发送N，并额外打开名字 ˜x的作 用域；相应的广播动作为˜M?(˜x)和M!(ν ˜x)N；还有静默动作 τ，它是一个输入动作和 一个输出动作之间通信的结果。当 ˜x为空时，我们通常省略(ν˜x)和(˜x)。

用于通信的连通性谓词也由实例化定义。这些条件包括通道等价谓词M ↔. N，该谓 词用于定义哪些项表示相同的单播信道，以及广播连接性谓词M≺.K和K. M，它们分 别用于在广播通道上的发送和接收：只有当在当前断言环境中存在M ≺. K时，项M才能 用于在通道K上发送广播消息，广播接收的情况类似（见第5节中的示例）。

例如，Pi代理
bc.Q | b(a).case a= b: a(z).R
具有标记为bc和b(x)的迁移，适用于所有名字x和 τ。输入前缀可以生成无限多个输入动作 （此处每个x对应一个）。为了避免这种无限分支，我们在工具中使用符号语义（参见第7节.1），其中实际值被变量所抽象。相反，每条迁移都有一个转换约束，该约束必须满足才能使 相应的非符号迁移成为可能。形式上，这些迁移写作P α →− C P′，其中C是一个转换约束。

先前代理的输入迁移在符号语义中可用单个迁移表示。为简便起见，我们展示输入前 缀子代理的前两个迁移：
P= b(a). case a= b: a(z).R
w(a) −−−−−→ { |1b↔.w|} case a= b: a(z).R
v(z) −−−−−−−−−−−→ { |1 a↔.v|}∧{ |1a=b|} R,
其中 w和 v是新的（形式语义见第7节）。第一次迁移的约束直观上表示通道 w等价于b （不一定总是存在这样的 w！）；对于第二次迁移，除了情况结构的条件外，还出现了类 似的约束。

我们可以使用PWB来模拟P的迁移。该工具使用智能体的ASCII表示，其中非字母数 字的项和条件必须用双引号括起来， ν写作new，输出对象写在角括号之间，输出中的上 划线用前面的单引号表示。例如，bf(a,c).(νx)Q写作’b< ”f(a,c)”>.(newx)Q。

代理P 的第一个迁移如下：

ACM嵌入式计算系统汇刊，第14卷，第1期，文章9，出版日期：2015年1月

Psi‐演算工作台 9:5

打印约束时，平凡的 1 会被省略。此处的“gna”表示一个新鲜名称，对应于 w：符号输入动作 的主语导。数选择”a= b”:a(x).R没有非符号迁移，因为a与b不是相同名称，但符号语 义在约束under theconstraint a=b下具有迁移。

约束{ |”a= b”| } 可通过将a替换为b来求解，如解行所述。该解由PWB中的约 束求解器模块生成，对于π‐演算实例，此模块执行名称合一（见第2节），类似于早期用 于π‐相关演算的工具（例如MWB）。在将解应用于代理后，会产生相应的非符号迁移。

除了符号执行外，PWB还包含一个符号检查器，用于计算一个代理与另一个代理（双） 相似的最小充分约束，以及一个见证关系。在对该约束应用一个解（如果存在的话）后， 这两个智能体将以非符号形式相关联。

3. 实现

Psi‐演算工作台（PWB）使用标准ML编程语言实现，并可在Poly/ML编译器[PolyML 2013] 版本5.4下编译。PWB是开源的，可从Gutkovas和Borgstr¨om [2013]的在线资源免费获取。

PWB 是ψ‐演算的一个模块化实现，既可作为建模工具使用，也可作为构建Ψ‐演算的 特定实例工具的库。作为建模工具使用时，用户通过命令解释器进行交互，该解释器提供 用于进程定义（手动或从文件导入）、进程环境操作、逐步执行符号（强和弱）迁移以及 符号双模拟检查（强和弱）的命令。第4节和第5节给出了此类用法的示例。接下来，我们 描述PWB 的实现以及在创建ψ‐演算实例时需要提供的模块。

3.1. Ψ‐演算实例化

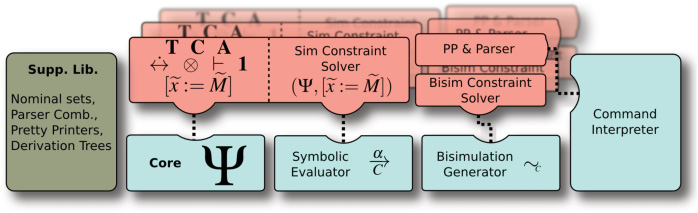
PWB为实例实现者实现了多个辅助库。我们在图1中展示了PWB的架构。在此图中，组件 之间的依赖关系从右向左：每个组件只能依赖于其上方或左侧的组件。所有组件都建立在 支持库之上，该支持库提供了ψ‐演算的基本数据结构和核心算法。实例实现者需提供实例 的参数、约束求解器以及解析和美化打印代码的定义。这些由用户实现的组件随后会被工 具实现的不同算法和命令解释器调用。并非所有组件都必须实现：例如，双模拟约束求解 器仅在进行双模拟检查时才需要。

实例的参数包括名称、项、条件和断言这几种类型，以及三类函数：定义逻辑的函数、 定义代换的函数和定义连通性的函数。作为类型的示例，以下是π‐演算的声明

ACM嵌入式计算系统汇刊，第14卷，第1期，文章9，出版日期：2015年1月

9:6 J. Borgstr¨om 等人

第2节中提到的实例。所呈现的所有SML代码均由实例实现者编写。

我们需要三个函数来定义实例的逻辑：蕴含（entails，或 ），用于描述在给定断言 下哪些条件为真；组合操作符（compose，或 ⊗），用于组合两个断言；以及单元断言 （unit，或1）。我们要求断言组合构成一个交换幺半群（模蕴含），并且所有函数都是等 变的，即它们对所有名字一视同仁。双模拟算法和弱符号语义还要求满足削弱性，即对于 所有′， ϕ蕴含 ⊗′ ϕ。

我们还需要等变的代换函数，用于在每一项、条件和断言中用项替代名字。

最后，我们有三个等变函数用于描述演算的连通性：chaneq（用于单播连通性）、 brTransmit 和 brReceive（用于广播）。通常，这些函数是简单地注入到条件类型中 （例如，funchaneq (M,N) = ChanEq (M,N)，其中 ChanEq 是条件的一个数据构造器）， 而连通性的定义则留给蕴含关系或约束求解器来完成。

通道等价chaneq需满足交换性和传递性（对每个）。brTransmit是广播输出连 通性. ≺，brReceive是广播输入连通性.；这些函数在第5节中举例说明。如果 蕴含 M . ≺ K 或 蕴含K . M，则要求出现在K 中的所有名字也必须出现在M中。

ACM嵌入式计算系统汇刊，第14卷，第1期，文章9，出版日期：2015年1月

Psi‐演算工作台 9:7

所有前述函数还需满足与代换可交换，即f(Xσ)=f(X)σ。

用户还需要为所调用的每种数据类型实现解析器 by t进程项的解析器。

3.2 符号执行

PWB通过sstep命令提供进程的符号执行。这是探索进程属性或模型本身的有用工具。在 此过程中，进程输入的值由变量表示，并在迁移推导过程中收集约束。这些约束显示了迁 移在何种条件下可能发生，尽可能延迟变量的实例化。强符号语义和弱符号语义（忽略 τ‐ 迁移）均可用（见第7节）。

在ψ‐演算中，包含断言的并行上下文（例如( | x = 3|)）可以启用额外的迁移。因此， 约束的一个解(σ,)由一个代换 σ（表示先前的输入）和一个断言 （表示并行上下文） 组成。直观上，每个解(σ,)求解为真，假没有解，同时是C 和C′ 的每个解都是C ∧ C′的解，而(ν ˜a){ |′ ϕ|}的解是形如(σ,)的对，其中 ⊗′σ ϕσ，且 ˜a 中的名 字不出现在 , σ中。

实例实现者可以为迁移约束提供一个约束求解器。该求解器应返回描述约束不可满足 性的字符串，或返回由代换和断言组成的解。由于迁移约束仅仅是原子约束的合取，通常 一个简单的基于合一的求解器就已足够。求解器的类型如下：

例如，第2节中π‐演算实例的求解器执行合一，通过迁移关系next实现。迁移系统中 的节点要么是形如(C σ)的对，要么是失败状态 ∅：
(ν a˜){ |1 T|} ∧ C, σ → C, σ
(ν a˜){ |1 a= a|} ∧ C, σ → C, σ
(ν a˜){ |1 a= b|} ∧ C, σ → ∅ if a = b∧(a ∈ a˜ ∨ b ∈ a˜)
(ν a˜){ |1 a= b|} ∧ C, σ → C[b:= a], σ[b:= a] otherwise.

3.3 符号（双）模拟

PWB还可用于检查进程上的模拟关系。例如，命令P˜ Q试图构造一个关联智能体P和Q的 互模拟关系。为此，我们实现了一个基于Johansson等人[2012]的符号互模拟算法（做了 一些修正和优化）。该算法接受两个进程，并生成扩展约束语言中的一个约束；这两个进 程在该约束的所有解下都是互模拟的。对于模拟检查，则使用该算法的一个简单变体。

互模拟约束语言还包含合取、析取和蕴涵，以及项等价 { | M = N|}、新鲜性{ |a#X|}（其 直观含义为“a在X中不是自由的”）和静态蕴涵约束。为了简化针对这种更丰富语言的约 束求解器的开发，PWB包含一个具有适当辅助函数的SMT求解器库。除非断言语言是平凡 的（仅包含单元断言），否则将迁移约束求解器扩展为互模拟约束求解器所需的大部分额 外工作都在于正确处理静态蕴涵约束。

ACM嵌入式计算系统汇刊，第14卷，第1期，文章9，出版日期：2015年1月。

9:8 J. Borgstr¨om 等人

4. 交替二进制协议

在本节中，我们描述了经典交替比特协议在PWB中的建模。这展示了如何使用PWB为特定 问题或问题领域定义量身定制的进程演算。我们还给出了PWB中符号化弱转换生成的一个 示例。

4.1. 交替位协议简介

交替二进制协议（ABP）[Bartlett 等人 1969]是一种通过有损辛道实现可靠数据传输的简单 网络协议。此处的“可靠”是指所有数据片段在接收方恰好被接收一次，并且顺序正确。考虑 一个发送方Sender、一个接收方Receiver，以及它们之间的两个通信通道：数据通道（ DataChan），用于发送数据片段；响应通道（ResponseChan），用于发送确认信号。我们 在图2中展示了这种情况：箭头表示数据传输的方向。ABP假设具备可靠的错误检测能力，但 不具备错误纠正能力。

为了确保接收方能够在存在丢包的通信信道下接收到每个片段，发送方会重复发送同 一片段，直到收到相应的确认信号，此时发送方才开始传输下一个片段。由于接收方不应 两次接受相同的片段，因此需要一种协议来区分各个包。在ABP中，每个数据包都附带一 个一位标志。第一个发送的数据包附带标志0；接收方对该包的确认信号也带有标志位0。 当发送方收到带有标志0的确认信号时，便知道接收方已正确接收该片段，随后发送方将开 始发送下一个带有标志位1的数据包，依此类推。因此，具有相同标志位的发送或接收的包 序列及其相应的确认信号均指向同一数据片段。

4.2. 一个用于 ABP 的估算演算实例

为了定义一个可表达ABP的估算演算实例，我们从数据项开始。由于该协议的行为不依赖 于所传输的数据，因此我们简单地将每个片段表示为一个名称。然而，协议本身需要一些 数据值和结构。

在项的集合中，我们包含通道DataChan和ResponseChan，以及值ERR，用于表示已检测 到错误。我们还有0和1比特，以及对它们的否定操作 ∼·，并具有预期的等式 ∼0= 1和 ∼1= 0。

我们对ABP的描述是无类型的，因此这些项构造符会产生不打算作为模型一部分的项， 例如 ∼ERR。这些虚假项会产生无效值 ⊥。总之，我们将数据项T定义如下：

ACM嵌入式计算系统汇刊，第14卷，第1期，文章9，出版日期：2015年1月

Psi‐演算工作台 9:9

在此及后续的显示中，符号表示列为数学符号表示，SML为实例实现者编写的代码，P WB是用户在工具中使用的实例所采用的ASCII语法。

接下来我们定义条件。在协议中，我们需要比较发送方或接收方的比特与传输的比特， 并检查在传输数据时是否发生了错误。为此，我们使用值上的相等性=。

我们添加一个恒成立的条件真和一个永不成立的条件假。最后，我们为单播通信引入 一个信道等价条件（ABP不使用广播，因此我们让广播连接性谓词返回假）：

我们不需要断言来建模ABP，因此我们令A={单位元}如第2节所述。

最后一步，我们定义项和条件上的代换函数。这些是标准的避免捕获的代换，随后根 据后文给出的项重写系统进行归一化。在计算弱迁移时，我们在代换后使用重写，以准确 检测 τ‐迁移的循环。这也极大地简化了约束求解器，因为范式比任意项更容易处理。

接下来，我们给出归约上下文 R::=[]|∼R下项的重写系统。它用于求值 ∼·操作符， 消除变量的双重否定，并识别虚假项。特别地，项 ∼∼ERR是虚假项，将被重写为 ⊥：
∼ERR → ⊥
∼⊥ → ⊥
∼0 → 1
∼1 → 0
∼∼x → x if x ∈N.

以下是关于条件的项重写系统。涉及虚假项 ⊥的等式被重写为假。注意，我们仅考 虑组成项已处于范式中的相等性条件；这已足够，因为条件上的代换函数是基于项上的代 换函数定义的：
∼x= ∼y → x= y
∼x= x → False
x= ∼x → False
M= N → True if M= N and{M, N} ⊆ Val ∪N
M= N → False if M = N and{M, N} ⊆ Val
M= N → False if ⊥ ∈{M, N}.

最后，我们需要定义蕴含。对于范式中的条件，我们定义如下
Unit a↔. b iff a= b
Unit M= N iff M= N
Unit True,
否则我们令单位元 ϕ 当且仅当 ϕ →+ ϕ′ → 且单位元 ϕ′

4.3. ABP迁移约束的约束求解器

ABP约束求解器是一个定义为迁移系统的标准合一算法。由于约束中的条件处于范式，其 设计得到了极大简化。

以下是统一转换系统。前两条规则是平凡的。关于通道等价↔.条件的规则，是π‐演 算求解器中所见的经典名字统一规则。最后的规则涉及相等性条件=。由于项处于范式， 我们知道其中一侧必定是一个名称，因此我们进行消元或交换以允许消元。接下来， ˜a# X d表示名字 ˜a在X中不自由出现；我们省略每个条件前面的 1 :
(ν a˜){ |True|} ∧ C, σ → C, σ
(ν a˜){ |False|} ∧ C, σ → ∅
(ν a˜){ |a↔. b|} ∧ C, σ → C, σ if a= b and a, b ∈N
(ν a˜){ |a↔. b|} ∧ C, σ → C[b:= a], σ[b:= a] if a˜#a, b and a = b
(ν a˜){ |a↔. b|} ∧ C, σ → ∅ otherwise
(ν a˜){ |a= M|} ∧ C, σ → C[a:= M], σ[a:= M] if a˜#a, M and a ∈N
(ν a˜){ |M= N|} ∧ C, σ →(ν a˜){ |N= M|} ∧ C, σ otherwise.

4.4. ABP 作为一个进程

这里我们给出了在之前定义的ABPpsi‐演算流实例中对ABP进行建模的过程。我们使用P WB语法给出该定义，这种语法由psi实例的用户所使用。

我们将图2中所示ABP的组件发送方和接收方建模为psi‐演算进程。组件数据通道 和响应通道的行为在我们的模型中被隐式地表示。为了组合系统，各组件分别具有输入和 输出通道inp和out。接收方和发送方各自还有一个额外的通道，分别用于向使用该协议 的应用程序输出o和输入i。

发送方的建模如下：首先在输入通道i上接收数据，然后递归地将数据与当前位b一 起在通道out上输出。接着，发送方在输入通道inp上接收确认位：如果确认位与b匹配， 则发送方翻转b并返回等待数据的状态；否则（如果位不匹配或发生错误），发送方会持 续尝试发送数据和b，直到接收到带有标志b的确认为止。

接收方以对偶的方式工作：

每个通道上都可能随时发生错误。这种不可靠的进程通过将名称（表示比特）视为变 量来隐式建模。由于传输的名称是变量，约束求解器可以通过找到合适的项进行替换，从 而在发送方或接收方中启用任意的选择子句。

隐藏内部通道后，ABP系统可以描述如下：

4.5. 一个弱转换示例

在研究ABP时，有趣的是观察该协议何时与外部系统进行通信，而忽略 τ‐迁移。我们在此展示了一 种这样的“弱”迁移，

ACM嵌入式计算系统汇刊，第14卷，第1期，文章9，出版日期：2015年1月

Psi‐演算工作台 9:11

其中发送方接收数据，并通过数据通道将其传输给接收方。我们对ABP 使用 wsstep命令，得到如下迁移之一：

迁移后，发送方（第13–16行）处于一种状态：它接收到的确认位与其自身的比特不匹配（第8行的约 束条件），从而使发送者发送的条件“b= ˜ackBit”（在此状态下为“sb= ˜rb”）变为真（第15行）。

该迁移是PWB生成的七个迁移之一。由于发送方和接收方始终有可能检测到错误E RR，因此它们之间会循环产生无限多个弱迁移。wsstep命令能够检测到此类循环（模α‐ 等价）。由于智能体中出现的项均处于范式，wsstep在ABP上会终止。

我们展示了在PWB中开发定制估算演算实例的过程。（完整的代码清单可在线获取[Gutkovas和Borgstr¨om 2013]。）通过这种方式，我们直接表达了比特及比特操作，并 且表明在代换函数中使用计算是可行且有益的，这不同于传统演算。我们还展示了弱转换 的符号模拟，这对应用很有帮助。

5. 无线传感器网络中的数据收集

在此示例中，我们研究一种用于无线传感器网络（WSNs）的数据采集协议 ) by在我们于PWB中实现的自定义Psi演算中对其进行建模。

无线传感器网络由大量传感器节点组成，用于感知环境数据。一个特殊的节点称为汇聚节 点，用于从网络中收集数据。数据收集通常采用多跳通信，构建以汇聚节点为根的路由树[Madden et al. 2002]。由于无线通信是不可靠的，每次协议运行时可能会构建不同的路由树。

我们提出了一种简单的算法来构建路由树：汇聚节点通过广播一条包含其标识符的特 殊初始化消息Sink来启动树构建。当一个节点n首次接收到初始化消息
时，它将其父节点parentn 设置为该消息的发送方，并广播一条包含自身标识符的新初始化消息，以继续 构建树的下一层。在树构建完成后，每个节点向其父节点发送一条包含其数据的数据消息。 此外，每个节点将被接收的数据消息转发给其父节点，确保数据最终到达汇聚节点。

ACM嵌入式计算系统汇刊，第14卷，第1期，文章9，出版日期：2015年1月

9:12 J. Borgstr¨om 等人

表示连通性，(b) 和 (c) 表示一些可能的路由树。)

5.1. 无线传感器网络数据收集的估算演算实例

我们首先定义并实现了一个自定义的ψ‐演算实例，适用于对前述树构建和数据采集协议进 行建模。我们使用两种类型的结构化信道：广播信道init(M)和单播信道data(M)。节点之 间的广播连通性由一个无向拓扑图给出。我们首先假设一个静态拓扑top；图3(a)的拓扑可 表示为top={(0,1),(0,2),(1, 2)}，其中汇聚节点ID为0。相应的Psi演算参数定义如下：

由于我们考虑的是静态拓扑，因此将断言实现为单位类型。具有主语init(i)的广播输 出前缀可以在广播信道init(i)上进行广播，而具有相同主语的输入前缀则可以从拓扑结构 中指定的任意连接的广播通道接收。两个单播前缀当且仅当其主语为相同名称时才可以通 信。因此，我们定义 如下：
init(M) . ≺init(N)当且仅当M= N ∈ N
init(M) . init(N)当且仅当M,N ∈ N 且（M,N） ∈或（N,M） ∈
数据(a) ↔.数据(b)当且仅当a= b ∈N.

5.2. 符号迁移的约束求解器

我们描述了迁移约束求解器的实现。我们用 ∅表示无解。迁移约束是条件的合取。这些 约束在两个阶段中求解，分别对应于单播连通性约束和广播连通性约束。为了简化求解器， 我们将进程中的所有自由名称视为互不相同（参见区分 [米尔纳等，1992b]）。对于单播 约束，如果约束不满足，则求解器失败（返回 ∅）。
(ν a˜){ |data(a) ↔. data(b)|} ∧ C → C if a= b
(ν a˜){ |data(a) ↔. data(b)|} ∧ C → ∅ otherwise.

约束求解器随后检查给定拓扑中的广播连通性。设O为输出约束 { |init(n) . ≺a|}，I为 输入约束 { |a . init(n)|}。我们区分四种不同的情况：
(1)如果I= ∅ 且O={{ |init(n)≺. a|}}，则解为[a:= init(n)]。
(2)如果I = ∅ 且O={{ |init(n)≺. a|}}，并且对于I中的每个约束{ |a.init(m)|} 都有(n,m) ∈ top，则解 为[a:= init(n)]。否则，该约束不可满足，即 ∅。
(3)如果I = ∅ 且O= ∅，则约束 求解器会找到n，使得对于每个{ |a. init(m)|} ∈ I，都有(n,m) ∈ top。对于每一个这 样的n，[a:= init(n)] 是一个可能的解。
(4)如果I= ∅且O= ∅，则该约束的广播部分 平凡成立。

5.3. 树构建模型

实例实现后，我们可以使用PWB语法定义用于建模树构建算法的进程。汇聚节点广播其自 身的通道，然后进入数据收集模式；即，它在其单播信道上重复监听：

一个节点在其广播信道上监听其父节点的通道，以便向该父节点发送数据。然后，类 似于汇聚节点，它广播自己的单播信道，期望通过该信道接收数据并转发给父节点。完成 广播后，它将数据发送给父节点，并进入数据转发模式：

5.4. 示例强迁移

我们在此研究由一个包含汇聚节点和两个传感器节点的小型无线传感器网络生成的（符号）迁移系 统。每个节点都有一个用于响应消息的唯一通道：

我们将展示在PWB中可能的迁移序列，使用图3(a)所示的拓扑。为了便于跟踪，我们仅 考虑标记为广播输出和单播通信动作的迁移。

通过执行PWB在System3 上的符号模拟器，得到以下初始迁移。结果系统处 于一种配置中，其中两个传感器节点均已获得父节点的通道，此处即汇聚节点的通道。随 后，这些节点将能够向汇聚节点传输其数据。单播通道连接性对应于图3(b)所示的路由树。 这是由PWB生成的七种可能初始迁移之一，其中三种表示从环境接收的广播，另外三种表 示并非所有节点都接收到广播消息的情况。迁移标签gna!(newbsChan)bsChan表示具有 新鲜名称gna的通道。生成的约束要求 { |init(0) . ≺ gna|} ∧ { |gna. init(1)|} ∧{ |gna. init(2)|}，意味着节点0输出连接到某个输入 连接到节点1和节点2。约束求解器找到该约束的一个解，该解将init(0)代入gna：

在导数中，汇聚节点成功将其单播信道chanS与两个节点进行了通信。

从这一点开始，系统可以通过两种对称的方式演化：任一节点都可以广播一条初始化消息， 但由于（封闭）系统中没有节点在广播信道上监听，该消息不会被接收。以下是节点1的迁移：

系统现在处于节点1可以向汇聚节点发送数据的状态。通过执行节点2的类似迁移，我们得 到一个系统，其中两个节点都已准备好通信数据：

ACM嵌入式计算系统汇刊，第14卷，第1期，文章9，出版日期：2015年1月

Psi‐演算工作台 9:15

我们展示了在PWB中使用高级特性的方法，例如使用具有不同通信模式（点对点与广 播）的结构化通道。广播连接图（拓扑）被形式化为一个断言；这使得我们有可能扩展模 型，例如支持动态或局部连通性。我们使用符号执行来模拟系统的强符号迁移。这些都表 明了PWB在建模和研究无线传感器网络算法方面的多功能性和实用性。

6. 无线传感器网络中的动态拓扑

我们在此将第5节的示例扩展到动态拓扑。我们首先允许向连通性图中添加边，然后加入删除边的对偶操作。

参数与第5节示例中的相同，除了断言外，现在的断言是一个表示拓扑中边的有限集元组：

蕴含关系保持不变，单播约束的约束求解器也相同。为了实现广播连通性，如果必要的边 不存在，求解器会尝试将其添加到解中（这在无线传感器网络的进程演算模型中是常见的 [Ghassemi 等人，2008；Godskesen 2010]）。例如，第5.4节中第一次迁移的约束在空 拓扑下的解为([gna:=”init(0)”],”(0,2),(0,1)”)。

接下来，我们增加代理从环境中删除边的能力。在断言中，我们将边建模为二元切换 器，因此如果同一条边出现两次，则等效于该边根本不出现（即{(M,N)} ⊗{(M, N)} 1）。 参数通过添加与边是否存在相对应的条件进行扩展，而断言则为有限多重集：

环境中奇数个边元组表示该边存在；偶数个表示不存在。因此，向环境中添加一个元 组可能会增加或删除一条边。我们通过以下蕴含定义来描述这一点：
conn(M,N)当且仅当M,N ∈ N 且 |(M,N)| + |(N, M)| 为奇数
disconn(M,N)当且仅当M,N ∈ N 且 conn(M,N)
init(M) . init(N)当且仅 当conn(M,N).

对于第5节中的协议，我们可以重用相同的约束求解器，但需注意它无法处理断开连接条件（ disconn condition）控制广播输入的情况。我们还可以通过以下两个智能体来表示拓扑结构的变化：

ACM嵌入式计算系统汇刊，第14卷，第1期，文章9，出版日期：2015年1月

9:16 J. Borgstr¨om 等人

代理Disconnect<1, 2> |( |”(1,2)”|)具有两条迁移：第一条为( |”(1,2)”|)| ( |”(1,2)”|)， 其约束条件 { |”(1,2)” |−”conn(1,2)”|}可平凡求解；第二条为 0|(|”(1,2)”|)，其解为([],” (1,2)”)。在这两条迁移中，环境均被扩展了一个额外的元组(1,2)，从而有效地从拓扑中移除 了一条边。直观上，智能体Connect和Disconnect可用于在全局表中设置和清除比特。

7. 符号语义

在本节中，我们描述了广播psi‐演算的符号操作语义，该语义相对于具体广播语义[Borgstr¨om等人提出的模型是可靠的（定理7.11）和完备的（定理7.12） 2011, 2013]。 该语义已在PWB中实现，并对Johansson等人提出的原始符号语义[2012]进行了扩展、简 化和修正。

7.1. 符号操作语义

正如我们所见，符号操作语义中的迁移形式为P α →− C Q ，其中C是迁移启用所需满足的约束。 每个PWB 实例实现一个求解器，用于计算该实例迁移约束的解。

定义 7.1（约束与解） 。 一个解是形如(σ,)的二元组，其中 σ 是将项代换为名字 的替换序列， 是一个断言。迁移约束（记作C,Ct）及其对应的解sol(C)定义如下：
约束解
C,C′ ::= 真 {(σ,) : σ是一个替换序列 ∧ ∈A}
| 假 ∅
| (νa)C {(σ,) : b#σ,, C ∧(σ,) ∈sol((a b) · C)}
| { |′ ϕ|} {(σ,) : ′σ ⊗ ϕσ }
| ∃x.C {(σ,) : y#σ,, C ∧([y := M]σ,) ∈sol((x y) · C)}
| a ∈n(M) {(σ,) : a ∈n(Mσ)}
| C ∧C ′ sol(C) ∩ sol(C′)

(a b)·C 表示在 C 中同时将 a 替换为 b 并将 b 替换为 a（“交换”）。在 (νa)C 中，a 在 C 中被 绑定；而在 ∃x.C 中，x 在 C 中被绑定。我们用 ∃ bx.C 表示 (νb)∃x.(b ∈n(x) ∧C)； ∃ 和 · ∈ n(·) 的唯一使用形式就是这种受限形式（该形式本身仅用于 表I 中的规则 SBRCLOSE）。我们采 用符号表示 (σ,) | = C 来表示 (σ,) ∈ sol(C)，并用 C ↔ D 表示 sol(C) = sol(D)。

转换约束C定义了一组解sol(C)，即通过应用代换并添加断言后使公式为真的那些解。例 如，转换约束 { |1 x= 3|} 的解为([x:= 3],1)和([], x= 3)，其中[]是恒等替换。 限制在逻辑合取上具有分配律，且逻辑合取以true为单位元并是结合的。因此，我们将在以下方程模 下考虑约束。
LEMMA 7.2 . (νa)(C1 ∧ C2) ↔(νa)C1 ∧(νa)C2 且 C1 ∧(C2 ∧ C3) ↔(C1 ∧ C2) ∧ C3 且 C ∧真 ↔ C.

ACM嵌入式计算系统汇刊，第14卷，第1期，文章9，出版日期：2015年1月

Psi‐演算工作台 9:17

代理 F(P)的框架概念在语义中被使用：直观上，它是代理的顶层断言，包括顶层绑 定器。框架的形式为F ::= | (ν a)，其中a在(νa)中被绑定。一个进程的框架表示其 对并行代理的贡献。例如，进程 F((νa)(( |1|) | M N . ( |3|) | ( |2|)))的框架是(νa)( 1 ⊗2)。注意3 未包含在框架中，因为它出现在前缀之下。为了定义符号操作语义， 我们需要一种将并行进程的框架添加到当前转换约束中的方法。

定义 7.3（向约束添加框架） 。我们按如下方式定义F ⊗C：
F ⊗(νa)C=(νa)(F ⊗ C) where a#F
(νa˜) ⊗ { |′ ϕ|}=(νa˜){ | ⊗′ ϕ|} where a˜#′, ϕ
(νa˜) ⊗ ∃x.C=(νa˜)∃x.( ⊗ C) where a˜#C and x#a˜,
F ⊗(C ∧ D)=(F ⊗ C) ∧(F ⊗ D)
F ⊗ C= C otherwise.

为了使符号语义能够识别出用于发送消息的原始通道，我们要求通道连接性在其左参 数上具有部分单射性：即要求对于所有名字a，函数x →(x ↔.a)是单射的。

如果一个进程P中出现的每个( ||)都是输入或输出的子项，则称该进程为断言保护。 要求进程是结构良好的：P是结构良好的˜，如果在P的每一个形如case ϕ˜:Q的子项中， 每个Qi都是断言保护的，并且在P的每一个形如!Q的子项中，Q是断言保护的。

我们令动作 α 的主语（或通道）为subj(x?(˜y))= subj(x(˜y))=˜ ˜ subj(x! (ν˜a)N)= subj(x (ν˜a)N)= x和subj(τ)= ∅。我们还定义标签的绑定名称 ˜（即私有名 称）为bn(x?(˜y))= bn(x(˜y))= ˜y和bn(x! (ν˜a)N)=˜bn(x (ν˜a)N)= ˜a以及bn(τ)= ∅。

结构化的符号操作语义保持结构良好性，并在表I、II和III中定义。我们首先描述表I 中的广播规则。首先 ˜ 考虑 SBROUT规则：M ˜N.P y! N −−−−−→ P。其转换约束{ |1M . ≺y|}的解 是使输出前缀的主语M能够在新鲜通道上进行广播的那些解

ACM嵌入式计算系统汇刊，第14卷，第1期，文章9，出版日期：2015年1月

9:18 J. Borgstr¨om 等人

{ |1 ⊗2 M1 ↔.M2|}) ∧(((ν˜c2)2) ⊗C1) ∧ (((ν˜c1)1) ⊗C2)。在 SOPEN 中，表达式 ν˜a∪{b} 表示将 b 插入到序列 ˜a 中任意位置。)

通道变量y。类似地，在 SBRIN中，我们可以从输入前缀的主语M能监听的任意通道x接 收一条广播。在SBRMERGE中，两个具有相同标签的输入被合并为一个。在SBRCOM中，Q接 收到P的广播，˜并将消息N代入输入变量 ˜y。名字˜a在P中被限制，因此它们必须对 Q是新的。在SBRMERGE 和 SBRCOM中，每个迁移的转换约束都扩展了另一个进程的帧。 在SBROPEN中，出现在消息N中的新名称˜b的作用域被打开；我们在转换约束中记录b 是新的。在SBRCLOSE中，已达到其词法作用域的广播转变为内部 τ动作。新名字˜a的作 用域被重新建立。

表II和表III中的其他符号规则与广播规则类似，但有两个例外。在表III的规则SCASE 中，我们将必须成立的约束 ϕi添加到迁移约束中。在表II的规则SCOM中，我们对输入和 输出迁移的迁移约束进行部分解构，提取出第一个合取项。然后重新组合迁移约束的剩余 部分，并添加它们的通道等价的约束（即1 ⊗2 M1 ↔. M2），得到Ccom。此处利用了 ↔.的部分单射性来保证M1是引发该迁移的通道。

7.2. 与原始符号操作语义的比较

本文使用的符号语义在四个方面与Johansson等人提出的原始语义[Johansson etal. 2012]存在显 著差异：
(1) 支持广播通信（表I）；
(2) 支持多体通信（一次发送多个消息项）；
(3) 不依赖外部断言环境（稍后）；以及 (4) 一个新的 SCOM规则，原因将在稍后 解释。

原始的通信规则如下（省略了其新鲜性侧条件）。接下来，断言环境“…”收集 当前进程上下文的断言，可以忽略：

为了推导出具有OLD‐SCOM的迁移，我们需要计算P和Q的框架，将框架中的绑定名称与出 现在˜ ˜迁移约束中的名称设为相等，使得 F(P)=(νbP)P 且 F (Q)=(νbQ)Q，然后验证1= 2= ⊗P ⊗Q。然而，在某些我们期望其成立的情况 下，这些等式却会失败。

例7.4 。此示例展示了与在进程构造子case和复制（!）下的限制相关的问题。我们以 复制为例；使用case时的情况类似。考虑π‐演算实例中的进程P=!(ν b)cb.Q。在原始 语义中，P的符号输出转换具有约束(ν b){ |1 c↔. x|}，因为推导中使用了(ν b)cb.Q的帧 （即(ν b)1）。当尝试推导P与进程c(x).R之间的通信时，OLD‐SCOM的侧条件˜F(P)=(ν bP)P无法满足： F(P)=(νε)1，而P的转换约束为(νb){ |1 c↔. x|}，因此绑定名称的数 量不同。

一个类似的问题，与帧中限制的顺序有关，出现在非活动并行进程具有顶层限制时。

例7.5 。设P=(ν b)cb.Q | (ν a)c(x).R。在原始语义中，P的符号输出转换具有约束 条件(νa)(ν b){ |1 c↔. x|}但 F(P)=(ν b)(ν a)1，其中绑定名称的顺序不同。

如果帧的约束符采用所谓的集合+约束符[Huffman 和 Urban 2010]（即顺序无关且忽 略冗余约束符），那么这两个问题都可以避免。然而，这种约束符的概念在用于ψ‐演算的 形式化[Bengtson 和 Parrow 2009]的 Nominal Isabelle [Urban 和 Tasson 2005]版 本中并不可用。

示例 7.6 。此示例展示了与断言组合为非交换的情况相关的问题。设断言为由名字组成 的元组 ˜a，使用˜连接 ˜a;b进行组合。考虑OLD‐SCOM的前提：在原始语义中， 1将具 有前缀Q;，而2 将具有前缀P;。由于连接是非交换的，若 P 和Q 非空且 n(P) = n(Q)，则OLD‐COM 的侧条件1= 2= ⊗P ⊗Q 无法成立。这使得两个 进程( |a|) | c和( |b|) | c无法通过OLD‐SCOM进行通信。

这些示例表明，规则OLD‐SCOM 对其前提中迁移约束的语法形式做出了过强的假设。 原始的符号语义在某些实例中仍然对应于具体语义 [Bengtson et al. 2011]，例如在通 信的进程不包含限制的情况下。

ACM嵌入式计算系统汇刊，第14卷，第1期，文章9，出版日期：2015年1月。

9:20 J. Borgstr¨om 等人

·X)[˜y：= ˜T] if ˜y#X ˜x)

⊇n(M)\ n(σ) n(M[˜a:= L˜]) ⊇ n( L˜) 当n(M) ⊇ ˜a (M . ≺N)σ= Mσ . ≺ Nσ (N .M)σ= Nσ . Mσ (M↔.N)σ= Mσ ↔. Nσ 1σ= 1 ⊗1 N ⊗′ N ′ ⊗ 1 ⊗(2 ⊗3) N(1 ⊗2)⊗3 ( ⊗′)σ N σ ⊗′σ ⊗1 N ⊗2当1 N 2)

断言组合满足交换幺半群定律（不仅仅是模断言等价）。与OLD‐SCOM不同，表II中的规则 S COM对绑定名称的数量或断言结构不做任何假设，而表I中相应的广播规则SBRCOM和 SBR MERGE对其约束的形式也完全不做任何假设。

7.3. 符号操作语义的正确性

符号语义相对于具体广播语义的可靠性与完备性的证明[Borgstr¨om 等人 2011]主要沿 用[Johansson 等人 2012]的方法。主要区别在于，他们对应的引理 7.10（描述迁移约束 的形状）并不在所有情况下成立，如示例 7.4、7.5 和 7.6 所示。我们在此通过考虑断言和 框架在冗余限制（参见示例 7.4）、限制顺序（参见示例 7.5）以及断言组合的交换幺半群 定律（参见示例 7.6）模下的情况，证明了一个较弱结果。

关于技术预备知识，我们假设表四中代换的一般性质，以及表 V 中的同态和名称保持 定律。例如，（名义）项代数中的标准代换概念满足所有这些性质。我们写作 N ′ iff n()= n(′)，并且对于所有 ϕ, 都有 ϕ iff′ ϕ。然后我们假设表 V 中的等价 关系。例如，当断言是关于项的有限方程集，并具有标准代换时，这些等价关系即被满足。

与原始证明的主要区别在于引入了框架上的一个辅助关系（定义 7.7），以准确描述 迁移约束的结构（引理 7.10），使得它们总能在规则 SCOM 中被分解，而不像 OLD‐SCOM 的情况。

定义 7.7（AC等价） 。 断言的结合/交换等价（AC等价）是最小的等价关系，使得
(1) 1 ⊗ ≡AC ；以及 (2) 1 ⊗2 ≡AC 2 ⊗1； 以及 (3) 1 ⊗(2 ⊗3) ≡AC(1 ⊗2)⊗3；以 及 (4) 1 ≡AC 2 ⇒ ⊗1 ≡AC ⊗2。
帧(ν˜a)1 和(ν˜c)2 是AC等价的，记作(ν˜a)1 ≡AC(ν˜c)2，如果 1 ≡AC 2且{˜a} ∩ n( 1)={˜c} ∩ n(2)。

LEMMA 7.8 . AC等价是框架上的一个等价关系，且当F1 ≡ACF2,时，也有n(F1)= n(F2)和(νa)F 1 ≡AC(νa)F2以及G ⊗F1 ≡AC G⊗F2。
PROOF 。根据定义直接得出，使用表 V 中的定律。

例如，受保护的进程具有与单位元帧1AC等价的框架。

LEMMA 7.9 .如果P是断言保护的，则 F(P) ≡AC 1。
PROOF 。对P进行归纳。

以下引理刻画了点对点输入和输出迁移的约束形式。约束中的第一个合取项始终是一 个通道等价约束（即原始前缀的对象M与迁移对象变量y之间的等价），该约束必须在某 个帧(ν˜c)下成立，且该帧与原始进程P的帧是AC等价的。该引理用于定理7.12的证明中， 以证明规则SCOM中迁移形状的前提条件始终成立。

LEMMA 7.10 (FORM OF CONSTRAINT) 。设 α=y (ν˜a) ˜N 或 α=y(˜x)。如果P →−α C P ′ 且 y#P，则存在 ˜c 、 M和D，使得 F(P)≡AC(ν˜c)，且y#˜c 、 M、 D以及C=(ν˜ c){ | M↔.y |} ∧ D。
PROOF 。根据P α →− C P′的推导进行归纳。一个基本情况如下。

SOUT 。在这种选择下，该迁移是由
SOUT
K N˜. P −−−y −N˜−→ { |1K↔.y|} P.
y#K, N˜, P
˜Here˜c= ε, = 1,M=K,和D=真,其中 F(KN .P)= 1.

需要使用AC等价的情况如下。

SCASE 。在这种选择下，迁移是由
SCASE
Pi α →− C P′
case ϕ˜: P˜ α −−−−−→ C∧{ |1ϕi|} P′.
bn(α)#ϕi
根据归纳，可得M,D′,,˜c，使得C=(ν˜c){ | M↔. y|} ∧ D ′，其中y#D′ 且 ˜F(Pi) ≡AC(ν˜c)。令D= D′ ∧ { |1 ϕi|}；由于y#选择 ϕ˜:P，因此也有y#D。根据结构良好性， Pi 是受保护的，因此根据引理7.9， F(Pi) ≡AC 1。由传递性得，F(P)= 1 ≡AC(ν˜c)。

SPAR 。在这种选择下，该迁移是由
SPAR
P α →− C P′
P | Q α −−−−→ F(Q)⊗C P′ | Q
bn(α)#Q
α= τ ∨ subj(α)#Q.
根据归纳，存在M,D{v1,}{v2,}˜c使得C=(ν˜c){ | M↔. y|} ∧ D ′，其中y#D′且 F (P) ≡AC(ν˜c)。令D= F(Q) ⊗ D′；由于y#P|Q，我们也有y#D。根据引理7.8， F(P | Q)≡AC((ν˜c))⊗F(Q) ≡AC F(Q) ⊗(ν˜c).

SSCOPE 。在此选择中，该迁移是由
SSCOPE
P α →− C P′
(νb)P α −−−→ (νb)C (νb)P′
b#α.
ACM嵌入式计算系统汇刊，第14卷，第1期，文章9，出版日期：2015年1月

9:22 J. Borgstr¨om 等人

=(νbP)P 且 F(Q)=(νbQ)Q，其 中bP对P˜bQ, Q,和 是新的，并且˜bQ 对Q˜bP, P,和 是新的。在规则 CPAR 中，我们假设 F(Q)=(ν˜bQ)Q,其中˜ bQ 对 ,P,和 α是新的。在规则 COPEN 和 CBROPEN 中，表达式 ˜a∪{b} 表示将b插入序列 ˜a中任意位置的结果。)

CBROUT
M≺. K
M!N˜. P −K−!− →N˜ P

CBRIN
K. M |x˜| = | N˜|
M?(x˜). P −K−?− →N˜ P[x˜:= N˜]

CBRMERGE
Q ⊗ P −K−?− →N˜ P′
P ⊗ Q −K−?− →N˜ Q′
P | Q K? N˜ −−−→ P′ | Q′

CBRCOM
Q ⊗ P K!(νa˜)N˜ −−−−−→ P′
P ⊗ Q K? N˜ −−−→ Q′
P | Q K!(νa˜)N˜ −−−−−→ P′ | Q′
˜bP˜bQ#K a˜#Q

CBROPEN
P K!(νa˜)N˜ −−−−−→ P′
(νb)P K!(νa˜∪{b})N˜ −−−−−−−−→ P′
b#a˜,, K b ∈ n(N)

CBRCLOSE
P K!(νa˜)N˜ −−−−−→ P′
(νb)P τ →−(νb)(νa˜)P′
b ∈ n(K) b#

COUT
M↔. K
M N˜. P K N