1 主要思想
- 将原始数据分成几个组
- 训练一组分类器,里面有很多种弱分类器
- 每个分类器的标签看作一次投票,投票最多的标签为最终标签
其架构如下所示:

2 为什么集成方法可行
假设这里有25个训练的弱分类器,且这些分类器独立工作,不会相互影响。
每一个分类器的出错率
集成分类器的最终做出一个错误预测的概率(超过一半的基础分类器都预测错了)为:
其中:X为做出错误预测的弱分类器的数量
由此可见,集成分类器做出一个错误预测的概率比弱分类器低很多。
下图显示了,弱分类器(有的文档也称base classifier)的错误率(做出错误预测的概率)与集成分类器(ensemble classifier)的错误率之间的关系

由上图可见,当弱分类器的错误率低于0.5时,集成分类器才有效。
集成分类器主要分为两种,一种处理数据的分布,例如bagging,boosting;
另一种处理输入特征,例如 random forests
3 Bagging Algorithm
3.1 Pseudo code

- 放回抽样(sampling with replacement)
3.2 实例
已知一维原始数据集:

弱分类器是一个单层决策树(desicion stump)

抽样,分类


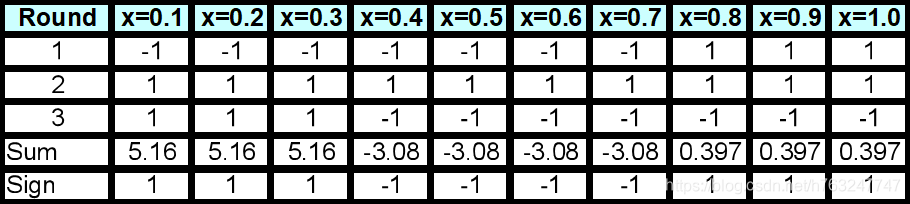
统计各标签的得票数(正票数+负票数):

上图中最后一行为预估类(或标签)
4 AdaBoosting Algorithm
4.1 Boosting
在bagging中,每一轮sampling,数据被取得概率都是一样的,而Boosting更加关注哪些被误分类的数据。
在Boosting算法中,首先,在第一轮Boosting中,所有的数据都被分配相同的权重(被抽取的概率),
在以后的几轮抽取中,被抽取的权重发生变化,错误分类的数据的被抽取的权重将会提升,
而正确分类的数据被抽取的权重将会降低。
4.2 AdaBoosting
4.2.1 Pseudo code

首先初始化权重w=1/n 并训练弱分类器:C1, C2, …, CT
其次,计算错误率:

计算一个分类器的重要性:

更新权重:

使所有
之和为1.
如果错误率高于0.5,所有权重再次被分配为1/n
分类公式:

4.2.2 实例
3.2中的一维原始数据集:

基本分类器任然是一个单层决策树(desicion stump)

训练数据过程:

总结:

计算权重:

分类:
预测分类的计算:

![]()
























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








