B树

https://www.bilibili.com/video/av36069871?from=search&seid=11071313654867248772我是根据这个视频来的。

为何要用到b树，原因是当数据量特别巨大时(操作系统的文件系统，数据库的索引),普通的搜索二叉树会导致树的深度非常的深，而b树是多路查找树，一个节点中有多个关键字(就是你需要的有效信息)，这样可以减少树的深度从而达到优化的作用。

我们先简单的看一下特性，首先是左边子树的值小于根节点的值，右子树的值都大于，中间子树在父子树两个关键之的值之间。

基本的概念就是这样，下面我们来说下2-3树和2-3-4树。

那么这个23和234是什么意思呢？这个叫做阶，意思就是一个b树中节点拥有多少个指向子节点的指针。

这是二阶

这是三阶

这是比较正规的说法，对于2树不允许有1个孩子，3树不允许有1或2个孩子要强调一下，b树的叶子节点要在同一层上，并且叶子节点的所有指针域都是null，这都是b树的一些性质。

这是非叶子节点的结构

n：该节点有多少个关键字

p:指向子树的指针

K:关键字

k1<k2<...<kn

k1<p1<k2

这都是很好理解的没关键是第三点每个节点至少含有[m/2]-1个关键字,这个很重要，也就是并非一个节点的关键字没有下限，这是与阶相关的。在后面的删除操作中异常的重要。

下面我们来构造一个b树，看看在构建时需要通过哪些手段让其变得具备上述性质。

首先给个数组 20，30，50，52，60，68，70 要求构建一个3阶的b树，我们先计算出节点最少和最多的关键字

最少:[3/2]-1=1 最多:[3-1]=2

当加入到50我们发现超过最大值了，这时，我们要用到分裂的手段。

分裂就是取n/2关键字作为新节点，然后将左右关键字作为子树

插入52

插入60

分裂

这里发现出现了不同，对于有父节点的树，需要向上合并，然后根据左右节点的大小进行插入。这里特别说明一下即便是合并了导致父节点关键字超过范围也要向上合并，下面会说处理方法。

插入68

70

然后我们分裂

我们发现父节点的关键词超出了最大值，怎么办呢？继续分裂

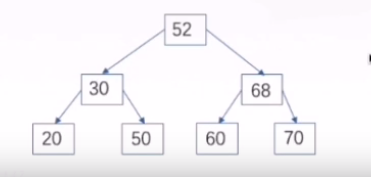
所以大家要注意这种连锁分裂的情况。

 

所谓的终端节点就是最下面一排的节点。

 

在这种情况下如果我们要删除2，如果直接删除的话会导致2这个节点的最小关键字没有达到要求，这时候我们要向兄弟节点取借一个关键字。但是同时要满足这个左小右大的条件，我们用7替换5的位置，再把5作为7的左节点。这就叫做兄弟够借的情况。

那么自然有兄弟不够借的情况，如果兄弟也是最小关键字，借了就会导致兄弟不够，这时我们要用到节点合并。

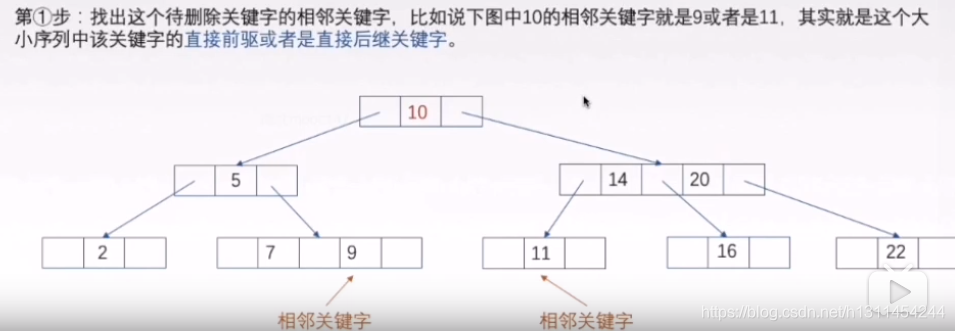
如果我们要删除16

如果直接删除了16会导致父节点的中间指针为null这不满足b树定义，那我们把父节点关键字给取消一个指针就是满的了，再把这个父节点的最小关键字放在最左子树的右侧，这就能满足b树的要求了。当然我把22和20合并了也是一种有效的方法，想法一致的。

这里采用的是9，因为9这个节点的关键字是大于最小的关键字数量的。

然后接下来就是第一种情况了，我们发现并不影响，所以直接删除就好了。

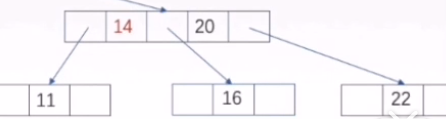例如我们要删除14    11和16都只有自已关键字，是最小关键字。

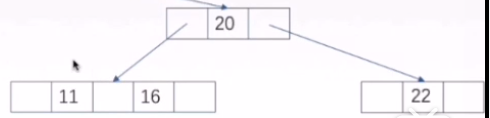
其实我们可以换一种思想我要删除14  ，14的相邻关键字是11和16，我们和11互换，然后删除14，实际上就是兄弟不够借的情况，采用向上合并的操作，得到的答案是一致的。