209. 长度最小的子数组（中等）

给定一个含有 n 个正整数的数组和一个正整数 target 。

找出该数组中满足其总和大于等于 target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。

示例 1：

输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。

示例 2：

输入：target = 4, nums = [1,4,4]
输出：1

示例 3：

输入：target = 11, nums = [1,1,1,1,1,1,1,1]
输出：0

思路：

滑动窗口双指针
首先两个指针都从0开始，两个指针分别为窗口的头和尾
用窗口的尾指针进行for循环遍历，每次累加一下，算总和在for循环中，因为累计加和要有终止条件，因此引入一个while循环，用来判断窗口里面的和是否>=目标值，while(sum>=target),在这里面用来移动窗口，首先算一下当前窗口的长度，窗口的和把原先头指针索引的值减掉，然后将窗口的头指针进行移动，继续进行while循环判断，如果还大于目标值，则继续移动头指针，按上面方法做，如果小于，则重新进行下一次for循环，说白了for循环是为了移动窗口尾指针，while是为了移动窗口头指针

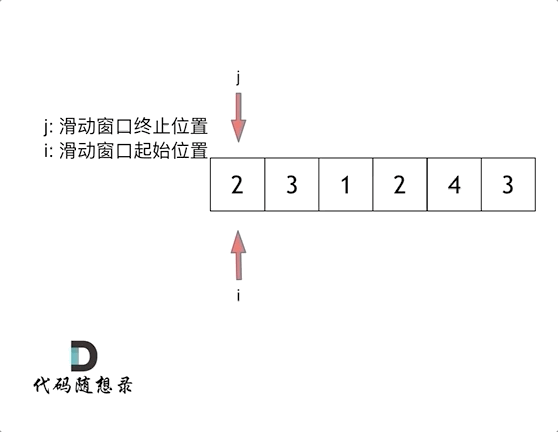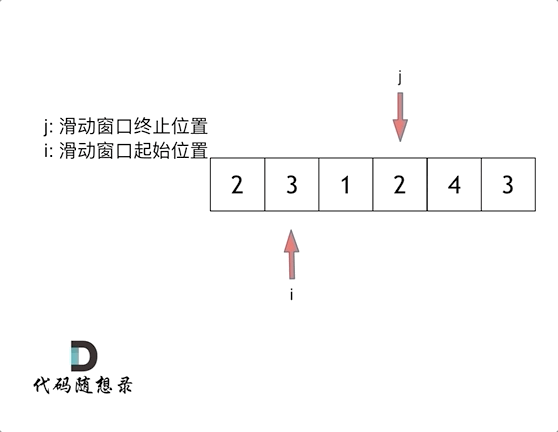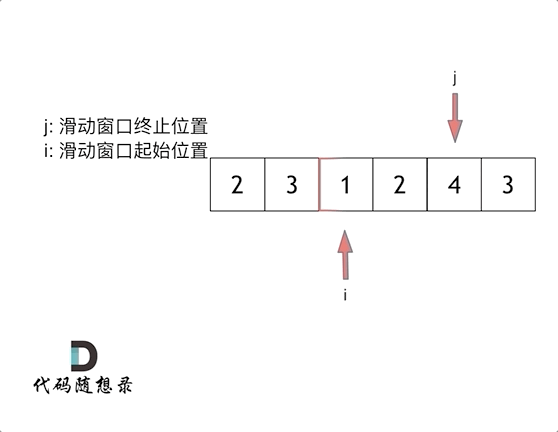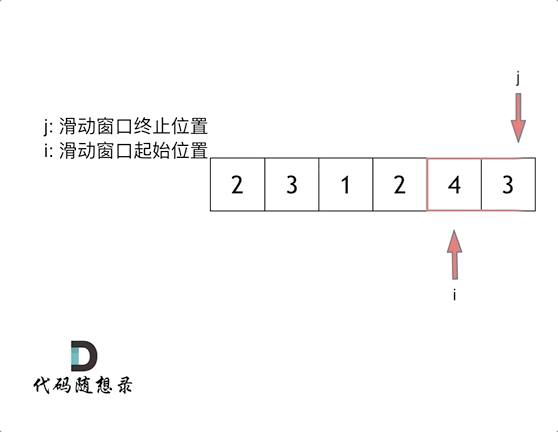
图片来源于代码随想录        

class Solution {
public:
    int minSubArrayLen(int target, vector<int>& nums) {
        int i=0,sum=0;
        int result=INT32_MAX;
        int temp=0;
        vector<int> end;
        for(int j=0;j<nums.size();j++)
        {
            sum+=nums[j];
            while(sum>=target)
            {
                temp=j-i+1;
                result=result>temp?temp:result;
                sum-=nums[i];
                i++;             
            }
        }
        if(result!=INT32_MAX)
        {
            return result;
        }
        else
        {
            return 0;

        }
       
    }
};