week1- Lecture2- asymptotic analysis

Algorithm efficiency: asymptotic analysis

一、Time Complexity Analysis

1. 如何衡量算法的运行时间

（1）编写算法并在计算机上运行，直接测量时间。然而，这种方法效率较低，因为运行时间会依赖于计算机的性能，并且测试慢速算法可能会浪费时间。

（2）更好的方法是分析算法中的重要步骤，并计算每个步骤需要执行多少次，与计算机的性能无关。

算法所需操作的数量通常是以输入规模为基础的 

2. 算法所需操作的数量通常是以输入规模为基础

Number of operations usually expressed in terms of input size

总共会有 n-1 次比较。

因此，时间复杂度 是 O(n-1)，这也可以简化为 O(n)

• 对于一个算法执行 5n - 3 次操作，时间复杂度依然是 O(n)，因为常数因子 5 和 -3 对输入规模 n 的影响是微不足道的。

因此，O(n-1) 和 O(n) 在时间复杂度分析中是等效的，我们通常直接表示为 O(n)。

二、Why efficiency matters?

尽管计算硬件的速度已经提高，但效率依然重要。随着计算机应用需求的增加，我们需要更高效的算法和解决方案来满足复杂任务的处理需求。

虽然速度提高了100倍，但由于算法本身的复杂度，能够处理的数据量并没有明显增加。

多个算法（A1, A2, A3, A4, A5）解决同一问题时的不同时间复杂度

不同复杂度的算法在不同数据量下的表现差异 

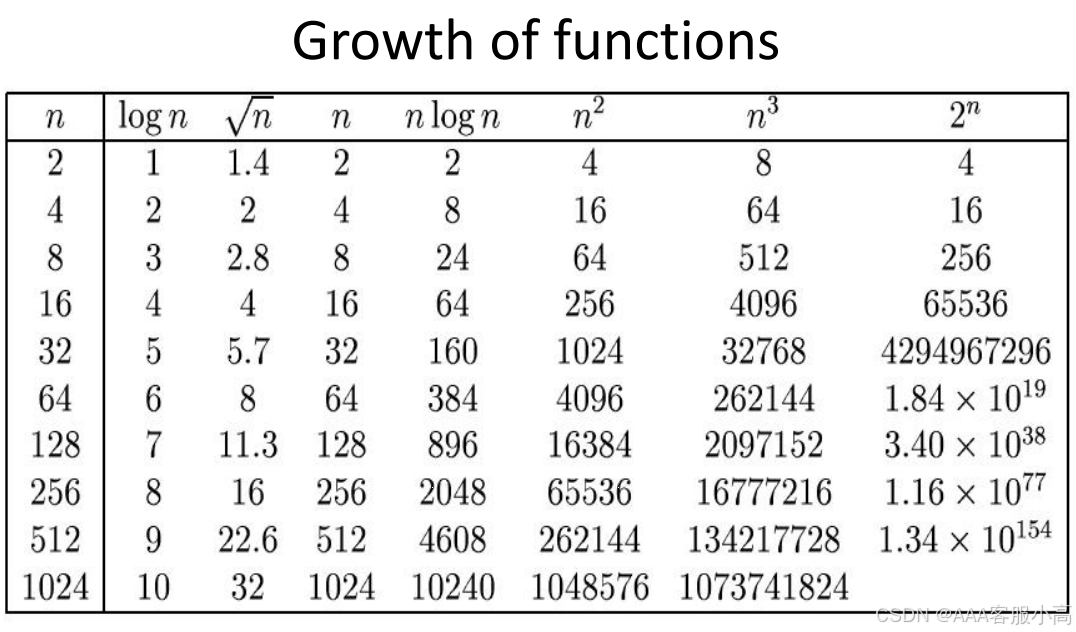
多项式时间复杂度和指数时间复杂度之间的差异

• 多项式函数（polynomial functions）（如 n, n log n, n² 等）：这些函数的增长速度较慢，通常是我们希望算法的复杂度属于这一类，因为它们随着数据量增加的速度较为平稳。

• 指数函数（如 2ⁿ）（exponential functions）：这些函数的增长速度非常快，随着数据量的增大，计算时间会迅速增加，通常会导致算法性能的严重下降。

– functions involving powers of n (e.g., n, n log n, n2 , called polynomial functions)

– functions involving powering by n (e.g., 2n , called exponential functions)

在多项式函数中，具有相同幂次的函数之间增长速度更接近，例如 f₃(n) = n² - 3n + 6 和 f₄(n) = 2n²，它们的增长速率非常相似。

Among polynomial functions, those with same order of power are more comparable

三、Hierarchy of functions

1. 这张图片展示了函数的层次结构，每个函数的增长速率都比前一个函数大。

each function has a greater order of magnitude than its predecessor.

successive functions have greater order of magnitude than the previous ones.

2. 可以通过在 n 和 n² 之间插入 n log n，或者在 n² 和 n³ 之间插入 n² log n 等方法进一步细化层次结构。refine the hierarchy

3. Relative Growth Rates

当 n 增加时，后面的函数的增长率大于前面的函数，说明增长率相对增加。

4. 我们可以为每个函数分配一个层次结构中的函数。比如 f(n) = 2n³ + 5n² + 4n + 7，其中最高次项是 2n³，因此 f(n) 的增长率由 n³ 主导。

The term with the highest power is 2n^3 .

The growth rate of f(n) is dominated by n^3

四、Big-O Notation

Big-O 记法用来表示算法的时间复杂度，它表示一个函数最多是另一个函数的常数倍。具体来说，f(n) = O(g(n)) 意味着，对于足够大的 n，f(n) 的增长不会超过 g(n) 的增长的常数倍。

this means f(n) is at most a constant times g(n) for all large n

1. Examples

不同函数的 Big-O 记法：

• 2n³ = O(n³)，表示 2n³ 的增长速率和 n³ 相同。

• 3n² = O(n²)，表示 3n² 的增长速率和 n² 相同。

• 2n log n = O(n log n)，表示 2n log n 的增长速率和 n log n 相同。

• n³ + n² = O(n³)，表示 n³ + n² 的增长速率由 n³ 主导，因此其时间复杂度是 O(n³)。

2. Big-O notation - formal definition

f(n) = O(g(n)): There exists a constant c and n₀ such that f(n) ≤ c g(n) for all n > n₀

 

 

n₀ 并没有一个固定的计算方法，它通常是通过理论推导和实验分析来估算出来的。

在  n < n₀  时，函数  f(n)  的值并不重要，因为 Big-O 分析只关注当数据量足够大时，算法的行为。

当  n  很小的时候，两者的关系不是特别明显，但随着  n  的增大， f(n)  的增长趋势逐渐与  c \times g(n)  一致。

• 渐近时间复杂度 （asymptotic time complexity）关注的是 大数据量（即  n  较大时）的复杂度表现。当输入规模足够大时，我们更关心算法随规模变化的增长速率，忽略了初期的一些常数项和不重要的低级增长。

when n is large

五、 Proof of order of magnitude（数量级）

 

 Exercise

6n²⁰ + 2ⁿ

The term with the highest degree is 2^n, so the order of magnitude is O(2ⁿ), not O(n²⁰). The answer is incorrect.