Arangodb最短路径查询语法

Arangodb最短路径算法只能确定一条最短路径。

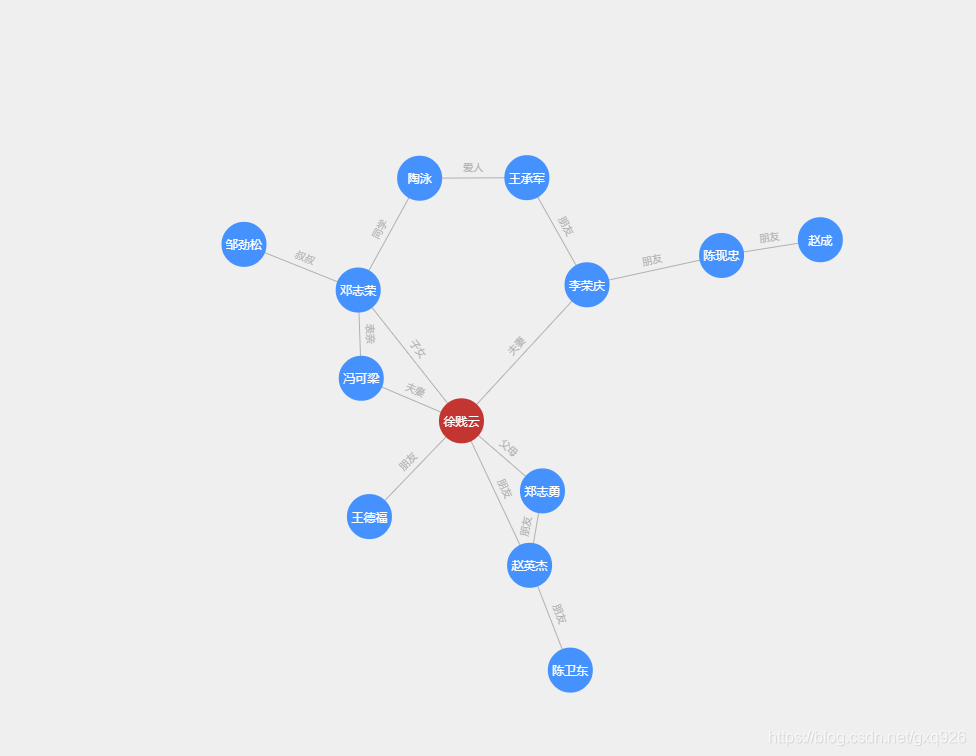
如图所示，我们从郑志勇到邓志荣的关系路径是：1、郑志勇–>徐贱云–>邓志荣 2、郑志勇–>徐贱云–>冯可梁–>邓志荣 3、郑志勇–>赵英杰–>徐贱云–>邓志荣 …

当然还有多条路径。我们可以从这些路径中可以看出除了第一条长度为3，其余的都大于3，而第一条就是我们要找的最短路径。

那么如果在arangodb如何来查询最短路径呢？假设我们有个people的vertex document即顶点文档,graph(图)为relation，然后查询如下：

FOR p IN OUTBOUND SHORTEST_PATH "people/郑志勇" TO "people/邓志荣" edges return p

这样就能查询出最短路径，结果就是：郑志勇–>徐建云–>邓志荣

总结

最短路径在关系图谱查询非常有用，可以去除不必要的关系找到最短的那条关系

参考：https://www.w2us.com/thread-237.htm