马尔科夫链（markov chain）

A Markov chain is “a stochastic model describing a sequence of possible events in which the probability of each event depends only on the state attained in the previous event.”

马尔科夫链虽然听上去很高深莫测，但其实它的概念还是很简单的：
1. 随机过程
2. 下一状态只依赖当前状态
举个例子：
一个袋子中有两个红球、一个绿球，不放回的取三次。这种情况下，第二次会受第一取法的影响，第三次会受前两次取法的影响。这是一个随机过程。如果将不放回取改为放回取，那每次取只取决于当前状态而不受之前状态的影响，这就是一个马尔科夫过程。

马尔科夫链是一系列状态之间的转移，对于马尔科夫链来说，一个重要的概念是转移矩阵。

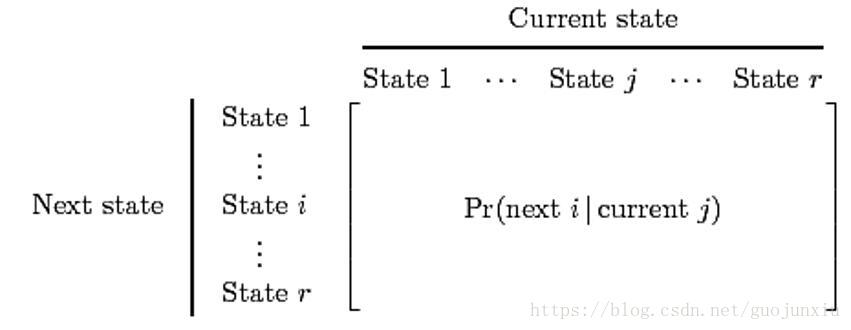
第i，j元素的意义是当前状态为 $j$，下一状态为 $i$，的概率。这种形式的矩阵每列概率和一定为1。

更常用的是一种转移矩阵是下列形式：

$P_{i,j}$表示当前状态为$i$, 下一状态为$j$的概率。这种形式的矩阵成为右随机矩阵(right stochastic matrix)

右随机矩阵的性质：

• 两个右随机矩阵的乘积仍然是仍然是一个右随机矩阵。
• 经过N步，状态$i$到状态$j$的概率为$(P^{N})_{i,j}$。
• 初始状态是一个行向量。
• 平稳概率向量$\pi$是不随转移矩阵运行而变化的矩阵，也就是说，它是转移矩阵的左特征向量，其特征值为1。
  $$\pi P = 1$$
  并可以观察到对任意 $i$ 我们都有以下极限而求出，
  $${\displaystyle \lim _{k\rightarrow \infty }\left(P^{k}\right)_{i,j}={\boldsymbol {\pi }}_{j},}$$
  其中 ${\displaystyle {\boldsymbol {\pi }}_{j}}$ 是行向量 $\pi$的第 个元素。