—数论—
一 、素数
1.素数筛法
(1) 线性筛选法——欧拉筛法
欧拉筛法通过红色标记部分保证每个合数只会被它的最小质因数筛去,时间复杂度降低到O(n)。
代码实现:`
#include <stdio.h>
#include <string.h>
#define MAXN 100000
#define MAXL 1000000
int prime[MAXN];
_Bool check[MAXL];
int main(void)
{
int n, count;
while (~scanf("%d", &n))
{
memset(check, 0, sizeof(check));
count = 0;
for (int i = 2; i <= n; i++)
{
if (!check[i])
prime[count++] = i;
for (int j = 0; j < count; j++)
{
if (i*prime[j] > MAXL)
break; // 过大的时候跳出
check[i*prime[j]] = 1;
if ((i%prime[j]) == 0) // 如果i是一个合数,而且i % prime[j] == 0
break;
}
}
for (int i = 0; i < count; i++)
printf("%d\n", prime[i]);
}
return 0;
}
2 小应用:求n的阶乘的因子数,题目n的范围(1000);
数论的原理,n的阶乘的因子个数等于n的素因子个数的幂的乘积;
代码实现:
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
int k[1005];
const LL mod=1e9+7;
int main()
{
int n;
cin>>n;
for(int i=2;i<=n;i++)
{
int l=i;
for(int j=2;j<=l;j++)
{
while(l%j==0)
{
k[j]++;
l/=j;
}
}
if(l) k[l]++;
}
LL sum=1;
for(int i=2;i<=n;i++)
{
if(k[i])
{
sum*=(k[i]+1);
sum=sum%mod;
}
}
printf("%lld\n",sum%mod);
return 0;
}
3.查找出小于等于MAXN的素数(生成连续素数表)
/*
* 素数筛选,查找出小于等于MAXN的素数
* prime[0]存素数的个数
*/
const int MAXN = 100000;
int prime[MAXN + 1];
void getPrime()
{
memset(prime, 0, sizeof(prime));
for (int i = 2; i <= MAXN; i++)
{
if (!prime[i])
{
prime[++prime[0]] = i;
}
for (int j = 1; j <= prime[0] && prime[j] <= MAXN / i; j++)
{
prime[prime[j] * i] = 1;
if (i % prime[j] == 0)
{
break;
}
}
}
}
4.同时得到欧拉函数表和素数表(线性筛)
/*
* 同时得到欧拉函数和素数表
*/
const int MAXN = 10000000;
bool check[MAXN + 10];
int phi[MAXN + 10];
int prime[MAXN + 10];
int tot; // 素数个数
void phi_and_prime_table(int N)
{
memset(check, false, sizeof(check));
phi[1] = 1;
tot = 0;
for (int i = 2; i <= N; i++)
{
if (!check[i])
{
prime[tot++] = i;
phi[i] = i - 1;
}
for (int j = 0; j < tot; j++)
{
if (i * prime[j] > N)
{
break;
}
check[i * prime[j]] = true;
if (i % prime[j] == 0)
{
phi[i * prime[j]] = phi[i] * prime[j];
break;
}
else
{
phi[i * prime[j]] = phi[i] * (prime[j] - 1);
}
}
}
return ;
}
二、GCD && exgcd
1.GCD: 公式:gcd(a,b) = gcd(b, a%b)
求a,b 最大公约数
代码实现:
ll gcd(ll a, ll b)
{
if(b == 0)
return a;
return gcd(b, a % b);
}
2.EXGCD:
公式: ax+by=c;
功能:用来解二元一次方程组;
注意事项:a,b均为正数;
取最小正整数解:
例题:。设青蛙A的出发点坐标是x,青蛙B的出发点坐标是y。青蛙A一次能跳m米,青蛙B一次能跳n米,两只青蛙跳一次所花费的时间相同。纬度线总长L米。现在要你求出它们跳了几次以后才会碰面。
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<vector>
#include<queue>
#include<stack>
#include<string>
#define LL long long
#define INF 0x3f3f3f3f
#define PI acos(-1.0)
using namespace std;
LL exgcd(LL a,LL b,LL &x,LL &y)
{
if(!b)
{
x=1;
y=0;
return a;
}
LL r=exgcd(b,a%b,x,y);
LL t=y;
y=x-(a/b)*y;
x=t;
return r;
}
int main()
{
LL a,b,x,y,n,m,l,k1,k2;//k2就是方程的一个x的解
cin>>x>>y>>m>>n>>l;
LL d=x-y;
a=l;
b=n-m;
LL c=exgcd(a,b,k1,k2);//c是最大公约数
if(d%c)//方程有解的条件
printf("Impossible");
else{
LL s=k2*d/c;
LL v=a/c;//对结果取余的最小的范围
printf("%lld\n",(s%v+v)%v);
}
return 0;
}
三、唯一分解定理
任何大于1的自然数,都可以唯一分解成有限个质数的乘积
例如对于大于1的自然数n,

这里Pi均为质数,其指数ai是正整数。
这样的分解称为的标准分解式。
1.找出一个数n的所有素因子
typedef long long ll;
ll fac[10050], num;//素因数,素因数的个数
void init(ll n) {//唯一分解定理
num = 0;
ll cpy = n;
int m = (int)sqrt(n + 0.5);
for (int i = 2; i <= m; ++i) {
if (cpy % i == 0) {
fac[num++] = i;
while (cpy % i == 0) cpy /= i;
}
}
if (cpy > 1) fac[num++] = cpy;
}
2.约数和定理&&约数个数定理
(1) 约数个数定理
约数个数定理可以计算出一个数约数的个数
根据唯一分解定理:

则n的正约数的个数就是

将378000分解质因数378000=2^ 4×3^ 3×5^ 3×7^1
由约数个数定理可知378000共有正约数(4+1)×(3+1)×(3+1)×(1+1)=160个。
代码实现
int prime[maxn],nprime;
int vis[maxn];
void getprime(){
nprime = 0;
memset(vis,0,sizeof(vis));
for(int i = 2; i <= 450; i++){
int t = 450/i;
for(int j = 2; j <=t; j++)
vis[i*j] = 1;
}
for(int i = 2; i <= 450; i++){
if(!vis[i])
prime[nprime++] = i;
}
}
int factor_count(int n){
int ans = 1,sum;
int k = sqrt(n*1.0);
for(int i = 0; prime[i] < k; i++){
if(n % prime[i] == 0){
sum = 0;
while(n % prime[i] == 0){
sum++;
n /= prime[i];
}
ans *= (a+1); //ans为n的约数的个数
}
}
if(n > 1)
ans *= 2;
return ans;
}
(2)约数和定理
n的(a₁+1)(a₂+1)(a₃+1)…(ak+1)个正约数的和为
f(n)=(p1 ^ 0+p1 ^ 1+p1 ^ 2+…p1^ a1)(p2 ^ 0+p2 ^ 1+p2 ^ +…p2 ^ a2)…(pk ^ 0+pk^1+pk ^ 2+…pk ^ ak)
代码实现:
int prime[maxn],nprime;
int vis[maxn];
void getprime(){
nprime = 0;
memset(vis,0,sizeof(vis));
for(int i = 2; i <= 450; i++){
int t = 450/i;
for(int j = 2; j <=t; j++)
vis[i*j] = 1;
}
for(int i = 2; i <= 450; i++){
if(!vis[i])
prime[nprime++] = i;
}
}
int pow_mod(int a,int n,int MOD){
int ans = 1;
while(n){
if(n&1)
ans = (ans*a)%MOD;
n >>= 1;
a = (a*a)%MOD;
}
return ans;
}
int factor_sum(int n){
int ans = 1,sum;
int k = sqrt(n*1.0);
for(int i = 0; prime[i] < k; i++){
if(n % prime[i] == 0){
sum = 0;
while(n%prime[i] == 0){
sum++;
n /= prime[i];
}
ans *= (pow_mod(prime[i],sum+1,MOD)-1)/(prime[i]-1);
}
}
if(n > 1)
ans *= ans(n*n-1)/(n-1);
return ans;
}
杜教筛:
有些时候也有一些奇形怪状的函数比如
,其中是pi质数,ai>0且
。
接着,出题人给了你一个挺大的n,n一般来说都有10^10左右。
最后,他想让你输出的值(可能会对一个大数取模)。
杜教筛差不多就是拿来解决这类问题哒…它给出了一个比较通用的技巧使得可以在或者
的时间复杂度内求的答案。
例如: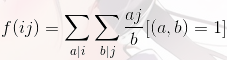
f(i,j)是一个积性函数,求前缀和,可以用杜教筛
#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include <tr1/unordered_map>
typedef long long ll;
using namespace std;
using namespace std::tr1;
const int P=1000000007;
const int inv2=(P+1)/2;
const int inv3=(P+1)/3;
const int maxn=1000000;
int prime[2000000],num;
int miu[maxn+5];
ll sumd[maxn+5],t1[maxn+5],t2[maxn+5]; int d[maxn+5];
inline void Pre(){
miu[1]=1; sumd[1]=1;
for (int i=2;i<=maxn;i++){
if (!d[i]) d[i]=prime[++num]=i,sumd[i]=1+i,t1[i]=1+i,t2[i]=i,miu[i]=-1;
for (int j=1;j<=num && (ll)i*prime[j]<=maxn;j++){
d[i*prime[j]]=prime[j]; int k=i*prime[j];
if (i%prime[j]==0){
miu[k]=0;
t2[k]=t2[i]*prime[j],t1[k]=t1[i]+t2[k],sumd[k]=sumd[i]/t1[i]*t1[k];
break;
}
miu[i*prime[j]]=miu[i]*miu[prime[j]];
sumd[k]=sumd[i]*sumd[prime[j]],t1[k]=1+prime[j],t2[k]=prime[j];
}
}
for (int i=1;i<=maxn;i++)
miu[i]=((ll)i*((P+miu[i])%P)%P+miu[i-1])%P,(sumd[i]+=sumd[i-1])%=P;
}
unordered_map<ll,int> S;
inline void add(int &x,int y){
x+=y; if (x>=P) x-=P;
}
inline int sum1(ll n){ return (n+1)%P*(n%P)%P*inv2%P;}
inline int sum1(ll l,ll r){ return (l+r)%P*((r-l+1)%P)%P*inv2%P; }
inline int Sum(ll n){
if (n<=maxn) return miu[n];
if (S.find(n)!=S.end()) return S[n];
int tem=1; ll l,r;
for (l=2;l*l<=n;l++) add(tem,P-l*Sum(n/l)%P);
for (ll t=n/l;l<=n;l=r+1,t--)
r=n/t,add(tem,P-(ll)sum1(l,r)*Sum(t)%P);
return S[n]=tem;
}
/*
inline int F(ll n){
int t1=0,t2=0; ll l,r;
for (l=1;l*l<=n;l++) add(t1,l%P*(n/l)%P),add(t2,sum1(n/l)%P);
for (ll t=n/l;l<=n;l=r+1,t--)
r=n/t,add(t1,(ll)sum1(l,r)*(n/l)%P),add(t2,(r-l+1)%P*sum1(n/l)%P);
return (ll)t1*t2%P;
}
*/
inline int F(ll n){
if (n<=maxn) return (ll)sumd[n]*sumd[n]%P;
int t1=0; ll l,r;
for (l=1;l*l<=n;l++) add(t1,l%P*(n/l)%P);
for (ll t=n/l;l<=n;l=r+1,t--)
r=n/t,add(t1,(ll)sum1(l,r)*(n/l)%P);
return (ll)t1*t1%P;
}
int main(){
ll n,l,r; int Ans=0;
freopen("t.in","r",stdin);
freopen("t.out","w",stdout);
Pre();
scanf("%lld",&n);
for (l=1;l*l<=n;l++) add(Ans,(ll)(Sum(l)+P-Sum(l-1))%P*F(n/l)%P);
for (ll t=n/l;l<=n;l=r+1,t--)
r=n/t,add(Ans,(ll)(Sum(r)+P-Sum(l-1))%P*F(n/l)%P);
printf("%d\n",Ans);
return 0;
}
黑科技之BM
线性递推式,给出前几项自动可得出n项的值;前面的不用动 ,只需更改main函数中的 初值
代码实现:
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <vector>
#include <string>
#include <map>
#include <set>
#include <cassert>
#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,n) for (int i=a;i<n;i++)
#define per(i,a,n) for (int i=n-1;i>=a;i--)
#define pb push_back
#define mp make_pair
#define all(x) (x).begin(),(x).end()
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
typedef vector<int> VI;
typedef long long ll;
typedef pair<int,int> PII;
const ll mod=1e9+7;
ll powmod(ll a,ll b) {ll res=1;a%=mod; assert(b>=0); for(;b;b>>=1){if(b&1)res=res*a%mod;a=a*a%mod;}return res;}
// head
int _,n;
namespace linear_seq {
const int N=10010;
ll res[N],base[N],_c[N],_md[N];
vector<int> Md;
void mul(ll *a,ll *b,int k) {
rep(i,0,k+k) _c[i]=0;
rep(i,0,k) if (a[i]) rep(j,0,k) _c[i+j]=(_c[i+j]+a[i]*b[j])%mod;
for (int i=k+k-1;i>=k;i--) if (_c[i])
rep(j,0,SZ(Md)) _c[i-k+Md[j]]=(_c[i-k+Md[j]]-_c[i]*_md[Md[j]])%mod;
rep(i,0,k) a[i]=_c[i];
}
int solve(ll n,VI a,VI b) { // a 系数 b 初值 b[n+1]=a[0]*b[n]+...
// printf("%d\n",SZ(b));
ll ans=0,pnt=0;
int k=SZ(a);
assert(SZ(a)==SZ(b));
rep(i,0,k) _md[k-1-i]=-a[i];_md[k]=1;
Md.clear();
rep(i,0,k) if (_md[i]!=0) Md.push_back(i);
rep(i,0,k) res[i]=base[i]=0;
res[0]=1;
while ((1ll<<pnt)<=n) pnt++;
for (int p=pnt;p>=0;p--) {
mul(res,res,k);
if ((n>>p)&1) {
for (int i=k-1;i>=0;i--) res[i+1]=res[i];res[0]=0;
rep(j,0,SZ(Md)) res[Md[j]]=(res[Md[j]]-res[k]*_md[Md[j]])%mod;
}
}
rep(i,0,k) ans=(ans+res[i]*b[i])%mod;
if (ans<0) ans+=mod;
return ans;
}
VI BM(VI s) {
VI C(1,1),B(1,1);
int L=0,m=1,b=1;
rep(n,0,SZ(s)) {
ll d=0;
rep(i,0,L+1) d=(d+(ll)C[i]*s[n-i])%mod;
if (d==0) ++m;
else if (2*L<=n) {
VI T=C;
ll c=mod-d*powmod(b,mod-2)%mod;
while (SZ(C)<SZ(B)+m) C.pb(0);
rep(i,0,SZ(B)) C[i+m]=(C[i+m]+c*B[i])%mod;
L=n+1-L; B=T; b=d; m=1;
} else {
ll c=mod-d*powmod(b,mod-2)%mod;
while (SZ(C)<SZ(B)+m) C.pb(0);
rep(i,0,SZ(B)) C[i+m]=(C[i+m]+c*B[i])%mod;
++m;
}
}
return C;
}
int gao(VI a,ll n) {
VI c=BM(a);
c.erase(c.begin());
rep(i,0,SZ(c)) c[i]=(mod-c[i])%mod;
return solve(n,c,VI(a.begin(),a.begin()+SZ(c)));
}
};
int main()
{
int T;
scanf("%d",&T);
while (T--)
{
vector<int>v;
v.push_back(3);
v.push_back(9);
v.push_back(20);
v.push_back(46);
v.push_back(106);
v.push_back(244);
v.push_back(560);
v.push_back(1286);
v.push_back(2956);
v.push_back(6794);
v.push_back(15610);
v.push_back(35866);
//VI{1,2,4,7,13,24}
ll n;
scanf("%lld",&n);
printf("%lld\n",linear_seq::gao(v,n-1));
}
}
斯特林近似公式:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define PI 3.1415926
ll n,t;
void solve()
{
ll a=(ll) ((0.5 * log ( 2 * PI * n) + n * log(n) - n-0.0005) / log(10));
printf("%lld\n",a+1); //是2 不是22,上传时貌似出问题了
}
int main()
{
scanf("%lld",&t);
while(t--){
scanf("%lld",&n);
solve();
}
return 0;
}//n! = sqrt((2 * n * PI) * (n / e ) ^ n)
卡特兰数
1.求n对括号合法的匹配的方式
C(n,2n)-C(n+1,2n)
2.卡特兰数公式
令h(0)=1,h(1)=1,catalan数满足递推式:h(n)= h(0)*h(n-1)+h(1)*h(n-2) + … +h(n-1)*h(0) (n>=2)
另类递推式[2]:h(n)=h(n-1)(4n-2)/(n+1);
递推关系的解为:h(n)=C(2n,n)/(n+1) (n=0,1,2,…)
递推关系的另类解为:h(n)=c(2n,n)-c(2n,n-1)(n=0,1,2,…)
3.可以利用卡特兰数解决的常见问题:
一个栈(无穷大)的进栈序列为1,2,3,…,n,有多少个不同的出栈序列?
在n*n的格子中,只在下三角行走,每次横或竖走一格,有多少中走法?
将一个凸n+2边形区域分成三角形区域的方法数?
圆上选择2n个点,将这些点成对连接起来使得所得到的n条线段不相交的方法数?
有2n个人排成一行进入剧场。入场费5元。其中只有n个人有一张5元钞票,另外n人只有10元钞票,剧院无其它钞票,问有多少中方法使得只要有10元的人买票,售票处就有5元的钞票找零?
代码实现:
#include <stdio.h>
#include<string.h>
int a[105][1000];//大数运算
int b[105]; //储存对应卡特兰数有多少位
void catalan() //求卡特兰数
{
int i, j, len, carry, temp;
a[1][0] = b[1] = 1;
len = 1;
for(i = 2; i <= 100; i++)
{
for(j = 0; j < len; j++) //乘法
a[i][j] = a[i-1][j]*(4*(i-1)+2);
carry = 0;
for(j = 0; j < len; j++) //处理相乘结果
{
temp = a[i][j] + carry;
a[i][j] = temp % 10;
carry = temp / 10;
}
while(carry) //进位处理
{
a[i][len++] = carry % 10;
carry /= 10;
}
carry = 0;
for(j = len-1; j >= 0; j--) //除法
{
temp = carry*10 + a[i][j];
a[i][j] = temp/(i+1);
carry = temp%(i+1);
}
while(!a[i][len-1]) //高位零处理
len --;
b[i] = len;
}
}
int main() {
catalan();
for(int i=1;i<=100;i++)
{
for(int j=b[i]-1;j>=0;j--)
{
printf("%d",a[i][j]);
}
printf("\n");
}
}




















 2237
2237

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








