2. AdaBoost算法

        AdaBoost是一个具有代表性的提升算法（Boosting）。

一、提升方法（Boosting）

（1）强可学习与弱可学习

        在概率近似正确（PAC）学习的框架中，一个概念（一个类）如果存在一个多项式的学习算法能够学习它，并且正确率很高，则称为这个概念是强可学习的；如果存在一个多项式的学习算法能够学习它，并且正确率仅比随机猜想略好，那么称为这个概念是弱可学习的。可以证明，强可学习与弱可学习是等价的。通常，发现弱可学习算法通常要比发现强可学习算法容易的多。

（2）提升方法

        提升方法是一种集成学习方法，其基本思想是：针对训练集，从若学习算法出发，反复学习，得到一系列地弱学习器，然后通过一定的结合策略组合这些弱分类器，形成一个强分类器。大多数提升算法都是改变训练数据的概率分布（权值分布）。针对不同的训练数据分布调用弱学习算法学习一系列弱分类器。

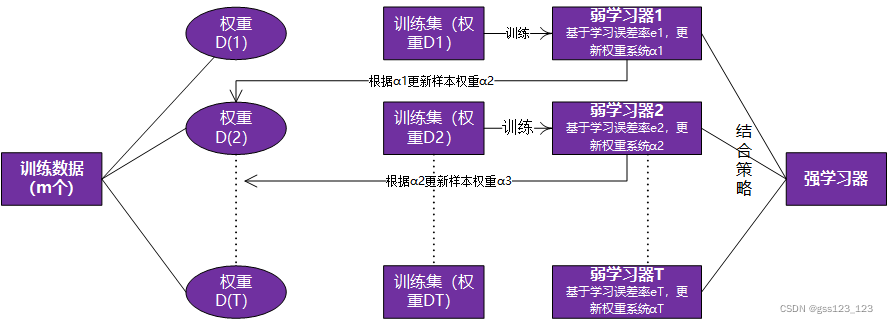
         提升算法的学习过程可以总结为：

        ① 初始化样本权重；

        ② 基于弱学习算法学习得到弱学习器，并基于损失函数最小化，更新样本的权值并计算弱分类器的权重系数；

        ③ 重复第②步操作，直到达到某个阈值；

        ④ 将上述得到的一系列的弱学习器按照一定的结合策略进行组合得到强学习器。

        对提升算法来说，需要解决两个问题：一是如何改变训练数据的概率（权值）分布；二是如何将弱分类器组合成一个强分类器。

        AdaBoost针对第一个问题，采取的策略是提高被错误分类的样本的权值，降低被争取分类的样本的权值；对于第二个问题，采用的加权多数表决方法，加大分类错误率低的弱分类器的权重，减小分类错误率高的弱分类器的权重。

二. 前向分步算法

       提升方法实际采用加法模型（即基函数的线性组合）与前向分步算法。

        加法模型如下：

        其中，表示基函数，是基函数的参数，是基函数的系数。

        在给定训练数据以及损失函数的情况下，学习加法模型成为经验风险最小化问题即损失函数极小化问题：

        这是一个复杂的优化问题，可以采用前向分步算法进行求解。前向分步算法的思路是：因为学习的是加法模型，如果能从前向后，每一步只学习一个基函数及其系数，逐步逼近目标函数，则可以简化优化问题的复杂度。每一步只需优化如下损失函数：

        前向分步算法的学习过程如下：

        输入：训练数据集，损失函数，基函数集；

        输出：加法模型