递归实现DFS全排列

​

问题

通过上一篇文章《return None来看递归函数流程解析》了解了递归函数的调用及执行之后，来看看如何应用吧。本篇文章将以DFS算法实现全排列为例，加深对递归的理解，顺便看看DFS算法中回溯（回退）机制的原理。

在正式开始之前，先来看看DFS算法及全排列的理论描述，如果对这部分已经掌握的读者，可以直接看下一个部分。

DFS算法通俗的讲就是一条道走到黑，再回头。以其典型的应用走迷宫为例。先选择一条路一直走下去，当走不通了，就回到上一个路口，看看还有没有其他可以走，有就继续往下走，没有就再倒退一个路口，直到走出迷宫或者走完所有路线。

全排列简单地说就是列出一个集合内所有元素的排列组合情况，高中知识就不赘述。那全排列如何与DFS算法结合呢？

以下题为例：

求出1,2,3,4四个元素的全排列

全排列的所有情况可以用树状图表示出来，图一中的红色数字1234便是其中一种排列情况。

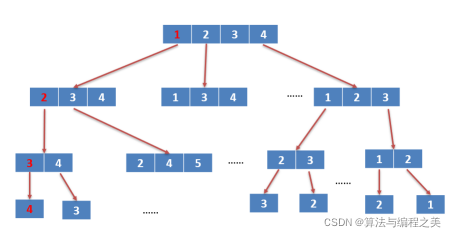
树状图也是图，根据DFS算法的思想，完全可以把图一视为一个迷宫，只是需要找的不是迷宫的出口&#x