首先放视频地址李宏毅老师深度强化学习视频。
上一篇初识Q-Learning讲了一些基础知识,本篇记录改进内容。
Double DQN
在DQN中,Q值总是会被高估,因为 Q ( s t , a t ) Q\left(s_{t}, a_{t}\right) Q(st,at)的target是 r t + max a Q ( s t + 1 , a ) r_{t}+\max _{a} Q\left(s_{t+1}, a\right) rt+maxaQ(st+1,a),估计的Q值中某个action的值偏高,在max操作时就很可能会选到这个。这样会导致Q值越估越大。因此有了Double Q-Learning的思想,即选取action的Q网络不变,选出action后,用另外一个网络 Q ′ Q^\prime Q′计算Q值。即target 为 r t + Q ′ ( s t + 1 , arg max a Q ( s t + 1 , a ) ) r_{t}+Q^{\prime}\left(s_{t+1}, \arg \max _{a} Q\left(s_{t+1}, a\right)\right) rt+Q′(st+1,argmaxaQ(st+1,a))这样就可以避免overestimate问题。在实作时,其实只需要里面max Q使用更新的network, Q ′ Q\prime Q′使用DQN中的target network。而不需要再增加新的网络。
Dueling DQN
这个tip是改network的架构,
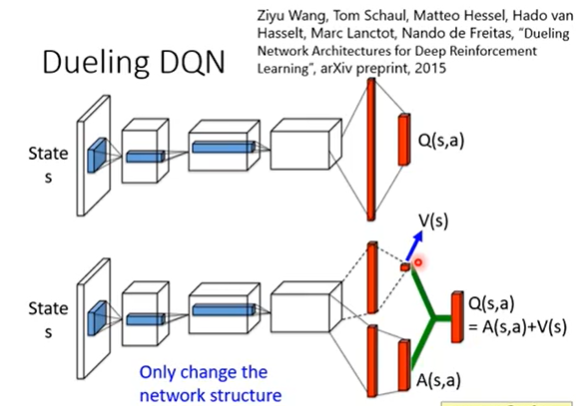
这样有时候直接改
V
(
s
)
V(s)
V(s)的值,就可以改变整个
Q
Q
Q,为了使网络更倾向于改
V
V
V而不是
A
A
A,文章给
A
A
A加了一些限制,比如某状态下
A
A
A值之和为零。这点在实作时就是加上了一个Normalization。
Prioritized Reply
改变从经验池里的采样方式。比如TD-error比较大的transition要较大概率地被采样到。
Multi-step(Balance MC and TD)
在TD方法中,我们只需要存下transition ( s t , a t , r t , s t + 1 ) \left(s_{t}, a_{t}, r_{t}, s_{t+1}\right) (st,at,rt,st+1),现在可以改成记录n-step的transition,如 ( s t , a t , r t , ⋯ , s t + N , a t + N , r t + N , S t + N + 1 ) \left(s_{t}, a_{t}, r_{t}, \cdots, s_{t+N}, a_{t+N}, r_{t+N}, S_{t+N+1}\right) (st,at,rt,⋯,st+N,at+N,rt+N,St+N+1),这样网络更新的设计就变为:
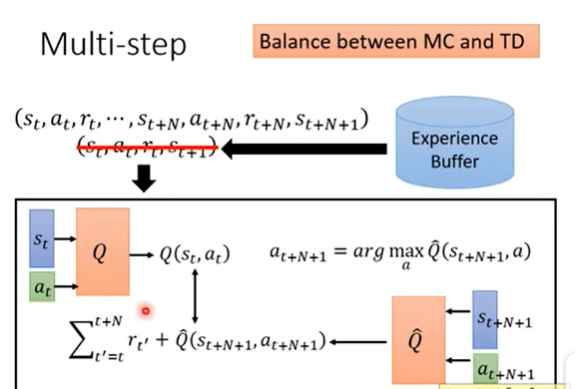
Noisy Net
Noise on Action (Epsilon Greedy)
就像上一节讲过的,在Action上加一个随机扰动。
a
=
{
arg
max
a
Q
(
s
,
a
)
,
with probability
1
−
ε
random,
otherwise
a=\left\{\begin{array}{cl} \arg \max _{a} Q(s, a), & \text { with probability } 1-\varepsilon \\ \text { random, } & \text { otherwise } \end{array}\right.
a={argmaxaQ(s,a), random, with probability 1−ε otherwise
这样给定同一个state,agent可能采用不同的action。
Noise on Parameters
a
=
arg
max
a
Q
~
(
s
,
a
)
a=\arg \max _{a} \tilde{Q}(s, a)
a=argamaxQ~(s,a)
其中,
Q
~
(
s
,
a
)
\tilde{Q}(s, a)
Q~(s,a)是用加噪声后的网络。
这种方法当遇到相同的state时,agent就会采取相同的action。(同一个episode,加的noise不变),称之为State-dependent Exploration。
Distributional Q-function
我们算的 Q π ( s , a ) Q^\pi(s, a) Qπ(s,a)其实是一个分布的期望,但是不同的分布(可能相差很大)的期望可能相同,这样用期望可能会损失一些信息。Distributional Q-function输出的不再是期望,而直接是原始的分布。这样能看到更细节的信息,比如某个 Q π ( s , a ) Q^\pi(s, a) Qπ(s,a)期望很大,方差也很大,表示采取这个行为平均收益较大,但也有很大的风险。
Q-Learning for Continuous Action
连续动作空间下不容易选出 a = arg max Q ( s , a ) a=\arg \max Q(s, a) a=argmaxQ(s,a),有以下几种思路:
-
采样法:
采样n个action,选出做大。这样不够精确。
-
利用梯度上升算法,parameter为a
运算量太大
-
重新构造网络使得
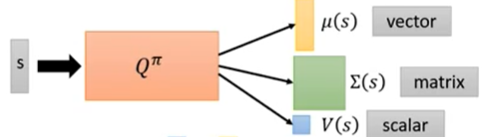
Q ( s , a ) = − ( a − μ ( s ) ) T Σ ( s ) ( a − μ ( s ) ) + V ( s ) Q(s, a)=-(a-\mu(s))^{T} \Sigma(s)(a-\mu(s))+V(s) Q(s,a)=−(a−μ(s))TΣ(s)(a−μ(s))+V(s)
这样就能满足 μ ( s ) = arg max a Q ( s , a ) \mu(s)=\arg \max _{a} Q(s, a) μ(s)=argmaxaQ(s,a)
 深度强化学习进阶
深度强化学习进阶





 本文深入探讨了深度强化学习的改进方法,包括DoubleDQN、DuelingDQN、PrioritizedReply、Multi-step、NoisyNet等策略,以及针对连续动作空间的Q-learning应用。通过这些方法,可以有效解决Q值过估问题,提高学习效率。
本文深入探讨了深度强化学习的改进方法,包括DoubleDQN、DuelingDQN、PrioritizedReply、Multi-step、NoisyNet等策略,以及针对连续动作空间的Q-learning应用。通过这些方法,可以有效解决Q值过估问题,提高学习效率。
















 1810
1810

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








