线段树模板

线段树

为什么需要线段树？
树状数组已经可以做到在含有单点修改的情况下，实现区间和的维护，其实先思路是利用两此查询的区间和相减得到指定区间的和
但是有些信息是无法通过相减得到的，例如最小值
这时就需要线段树来进行相关信息的维护了
线段树可以在O（logn）的时间内维护区间的信息
支持单点修改，区间修改，区间查询（区间求和，区间求最小值，区间求最大值等）

线段树维护的信息需满足可加性

区间的积，和，最值都满足可加性，区间的中位数不满足可加性

线段树的基本结构

线段树将每个长度不唯一的区间划分成左右两个区间递归求解，把整个线段划分为一个树形结构，通过合并左右区间的信息来求得区间的信息。这种数据结构可以方便的进行大部分操作。

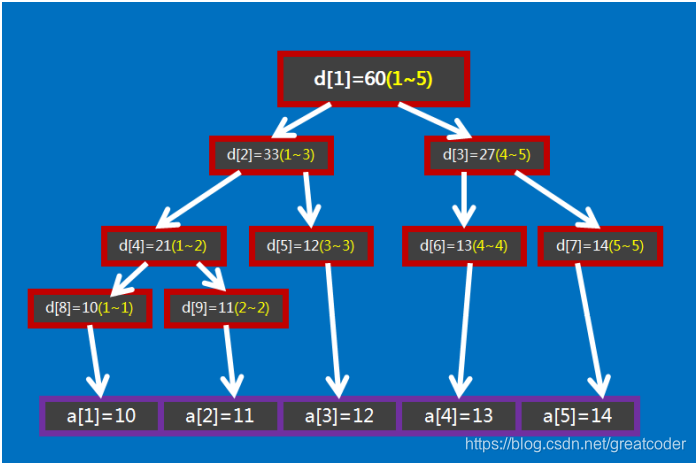
线段树的根维护 [ 1, n ] 区间
若当结点维护的区间为[ l , r ] , 定义m = ( l + r ) / 2
其左孩子维护的区间为[ l, m ]
其右孩子维护的区间为 [ m + 1, r ]
若当前阶段维护的区间长度为1，则指为线段树的初值,对应的数组的值

线段树的建立

递归建立，先建立孩子节点的，在建立父节点的
若一个结点标号为x ，其左孩子结点的标号为 2 * x ，右节点的标号为 2 * x + 1
当区间长度为 1 时，到达递归的边界，此时采用初值更新区间的值并返回.

//这是一个加和线段树
 long long  a[MAXN],d[MAXN<<2];
 void build(int x,int l,int r){
     if(l ==r){
         d[x] = a[l];
         return;
     }
     int m = (l + r)/2;
     build(x*2,l, m);
     build(x*2 + 1, m+1, r);
     d[x] = d[x * 2] +  d[x * 2 + 1];
 }

线段树的单点修改

只需找到相应的叶子节点，更新其值，在返回时维护经过的结点的值

int position;
 long long v;
 //将position的位置加v
 void upd(int x,int l,int r)
 {
     if( l== r)
     {
         d[x] += v;
         return;
     }
    int m = (l + r ) /2 ;
    if( position <= m) upd(x * 2, l, m);
    else upd(x * 2 +1, m + 1,r);
   
    d[x] = d[x*2] + d[x * 2 + 1];
 }

线段树的查询

//查询[p1， p2]的答案
 long long  ask(int x,int l,int r,int p1,int p2){
     // 要查询的区间刚好是当前区间，直接返回
     if(l == p1 && r == p2) return d[x];
     int m = (l + r) /2;
     //情况一 要查询的区间完全在左边的区间
     if(p2 <= m) return ask(x * 2, l, m, p1, p2);
    //情况二 要查询的区间完全再右边的区间
    else if(p1 > m) return ask(x * 2 + 1, m + 1, r, p1, p2);
    //情况三 要查询的区间分布在做有两个便，分别计算，合并后作为答案
    else {
        long long  lch_val = ask(x* 2, l, m, p1, m);
        long long  rch_val = ask(x * 2 + 1,m +1 ,r, m+1,p2);
        return lch_val + rch_val;
    }
 }