【一文了解】八大排序-归并排序、快速排序

如何理解时间复杂度为O(nlogn)？可以将分治过程想象成一棵二叉树：

    根节点：规模 n 的问题，耗时 O(n)（合并时间）。

    第 1 层子节点：2 个规模 n/2 的问题，总耗时 2×O(n/2) = O(n)。

    第 2 层子节点：4 个规模 n/4 的问题，总耗时 4×O(n/4) = O(n)。

    ...

    第 log₂n 层：n 个规模 1 的问题，总耗时 n×O(1) = O(n)。

    整棵树共 log₂n + 1 层，每层总耗时均为 O(n)，因此总时间为 O(n) × logn = O(nlogn)。

    注意：算法复杂度分析的核心是忽略常数因子（只关注增长趋势），因此 log₂n、log₁₀n、logₑn 在复杂度中被视为“等价”，统一记为 logn。

2）空间复杂度：

●递归：O(n + logn)（O(n) 用于合并时的临时数组，O(logn) 为递归调用栈深度）；

●非递归：O(n)（仅需临时数组，无递归栈消耗）。

4.稳定性

稳定（合并时，相同元素按子数组顺序保留，不改变相对位置）

1.5.举例（升序为例）

1）核心动作拆解

●分：将原数组递归拆分为两个等长（或近似等长）的子数组，直到每个子数组只包含 1 个元素（长度为 1 的数组天然有序）。

●治：当子数组无法再拆分时（长度为 1），开始合并。将两个有序的子数组合并为一个更大的有序数组，

●重复分治：重复分治过程直到合并出原数组长度的有序数组。

2）实例分析（[8,4,5,7,1,3,6,2]）

阶段 1：拆分（Divide）

    将数组不断二分，直到每个子数组长度为 1：

    原始数组：[8,4,5,7,1,3,6,2]

    拆分为： [8,4,5,7] 和 [1,3,6,2]

    继续拆： [8,4] [5,7] 和 [1,3] [6,2]

    最终拆分：[8] [4] [5] [7] 和 [1] [3] [6] [2]（共8个长度为1的子数组）

阶段 2：合并（Merge）

    从最小的子数组开始，两两合并为有序数组，逐步扩大规模：

    第 1 轮合并（长度 1 → 长度 2）

        合并 [8] 和 [4] → 比较 8 和 4 → 有序数组 [4,8]。

        合并 [5] 和 [7] → 比较 5 和 7 → 有序数组 [5,7]。

        合并 [1] 和 [3] → 比较 1 和 3 → 有序数组 [1,3]。

        合并 [6] 和 [2] → 比较 6 和 2 → 有序数组 [2,6]。

        合并后得到 4 个长度为 2 的有序数组：[4,8]、[5,7]、[1,3]、[2,6]。

    第 2 轮合并（长度 2 → 长度 4）

        合并 [4,8] 和 [5,7]：

            用双指针分别指向两个数组的开头（i=0 指向 4，j=0 指向 5）。

            比较 4 和 5 → 4 更小，放入临时数组[4]，i=1。

            比较 8 和 5 → 5 更小，放入临时数组[4,5]，j=1。

            比较 8 和 7 → 7 更小，放入临时数组[4,5,7]，j=2（j 越界，退出）。

            将剩余元素 [8] 放入临时数组 → 结果 [4,5,7,8]。

        合并 [1,3] 和 [2,6]：

            比较 1 和 2 → 1 更小，放入临时数组[1]，i=1。

            比较 3 和 2 → 2 更小，放入临时数组[1,2]，j=1。

            比较 3 和 6 → 3 更小，放入临时数组[1,2,3]，i=2（i 越界，退出）。

            将剩余元素 [6] 放入临时数组 → 结果 [1,2,3,6]。

        合并后得到 2 个长度为 4 的有序数组：[4,5,7,8]、[1,2,3,6]。

    第 3 轮合并（长度 4 → 长度 8）

        合并 [4,5,7,8] 和 [1,2,3,6]：

            双指针 i=0（指向 4）、j=0（指向 1）。

            比较 4 和 1 → 1 更小，放入临时数组[1]，j=1。

            比较 4 和 2 → 2 更小，放入临时数组[1,2]，j=2。

            比较 4 和 3 → 3 更小，放入临时数组[1,2,3]，j=3。

            比较 4 和 6 → 4 更小，放入临时数组[1,2,3,4]，i=1。

            比较 5 和 6 → 5 更小，放入临时数组[1,2,3,4,5]，i=2。

            比较 7 和 6 → 6 更小，放入临时数组[1,2,3,4,5,6]，j=4（j 越界，退出）。

        将剩余元素 [7,8] 放入临时数组 → 最终结果 [1,2,3,4,5,6,7,8]。

1.6.代码实现

归并排序的递归实现和非递归实现。

/// <summary>
/// 归并排序（分治思想）
/// </summary>
/// <param name="arr">待排序数组（会直接修改原数组）</param>
/// <param name="isAscending">排序方向：true=升序，false=降序</param>
/// <param name="isRecursive">是否递归实现</param>
public static void MergeSort<T>(T[] arr, bool isAscending = true, bool isRecursive = false) where T : IComparable<T>
{
    if (arr == null || arr.Length <= 1) return;
    if (isRecursive)
        MergeSortRecursive(arr, 0, arr.Length - 1, isAscending);
    else
        MergeSortIterative(arr, isAscending);
}
/// <summary>
/// 递归归并排序：二分数组并合并
/// </summary>
/// <param name="arr">原数组</param>
/// <param name="left">当前处理区间左边界</param>
/// <param name="right">当前处理区间右边界</param>
/// <param name="isAscending">排序方向：true=升序，false=降序</param>
private static void MergeSortRecursive<T>(T[] arr, int left, int right, bool isAscending) where T : IComparable<T>
{
    //递归终止条件：区间内只有1个元素（已序）
    if (left >= right) return;

    //1.二分区间（避免溢出）
    int mid = (left + right) / 2;

    //2.递归排序左半区间和右半区间
    MergeSortRecursive(arr, left, mid, isAscending);
    MergeSortRecursive(arr, mid + 1, right, isAscending);

    //3.合并两个已序子数组
    Merge(arr, left, mid, right, isAscending);
}
/// <summary>
/// 合并两个已序子数组
/// </summary>
/// <param name="arr">待排序数组</param>
/// <param name="left">左子数组开始索引</param>
/// <param name="mid">左子数组结束索引</param>
/// <param name="right">右子数组结束索引</param>
/// <param name="isAscending">排序方向：true=升序，false=降序</param>
private static void Merge<T>(T[] arr, int left, int mid, int right, bool isAscending) where T : IComparable<T>
{
    //1.创建临时数组，存储合并结果
    T[] temp = new T[right - left + 1];
    int i = left;//左子数组指针
    int j = mid + 1;//右子数组指针
    int k = 0;//临时数组指针

    //2.按排序方向，依次将两个子数组的小/大元素放入临时数组
    while (i <= mid && j <= right)
    {
        int compareResult = arr[i].CompareTo(arr[j]);
        bool takeLeft = isAscending ? (compareResult <= 0) : (compareResult >= 0);

        if (takeLeft)
        {
            temp[k++] = arr[i++];//取左子数组元素
        }
        else
        {
            temp[k++] = arr[j++];//取右子数组元素
        }
    }

    //3.将左子数组剩余元素复制到临时数组
    while (i <= mid)
    {
        temp[k++] = arr[i++];
    }

    //4.将右子数组剩余元素复制到临时数组
    while (j <= right)
    {
        temp[k++] = arr[j++];
    }

    //5.将临时数组的有序结果复制回原数组的对应区间
    Array.Copy(temp, 0, arr, left, temp.Length);
}
/// <summary>
/// 非递归（迭代）归并排序：原地合并优化，无需递归栈
/// </summary>
/// <param name="arr">待排序数组（原地排序，仅需临时数组存储合并结果）</param>
/// <param name="isAscending">排序方向：true=升序，false=降序</param>
public static void MergeSortIterative<T>(T[] arr, bool isAscending = true) where T : IComparable<T>
{
    int n = arr.Length;
    //核心：按“区间步长”迭代合并，步长从1开始（1个元素的区间天然有序）
    //步长每次翻倍（1→2→4→8...），直到步长≥数组长度
    for (int step = 1; step < n; step *= 2)
    {
        //遍历数组，按当前步长划分“相邻两个区间”并合并
        //每次处理两个区间：[left, mid-1] 和 [mid, right]
        for (int left = 0; left < n; left += 2 * step)
        {
            //计算第一个区间的右边界（mid = left + step）
            int mid = left + step;
            //计算第二个区间的右边界（right = left + 2*step -1），避免超出数组长度
            int right = Math.Min(left + 2 * step - 1, n - 1);

            //若mid > right，说明第二个区间为空（只剩一个区间），无需合并
            if (mid > right)
                continue;

            //合并两个有序区间：[left, mid-1] 和 [mid, right]
            Merge(arr, left, mid - 1, right, isAscending);
        }
    }
}

2.快速排序

2.1.核心逻辑

①选基准（如选区间最右边元素为基准）；②分区（将数组分为"小于/大于等于基准"的两部分）；③递归排序两部分（直至子数组长度为 0 或 1）

2.2.适用场景

不稳定（分区交换时，相同元素可能被交换到基准两侧，破坏相对位置）

2.3.复杂度

1）时间复杂度：O(nlogn)（平均/最优）、O(n²)（最坏，如已排序数组选两端为基准）

2）空间复杂度：O(logn)（递归栈深度，平均logn层）

2.4.稳定性

不稳定（分组排序时，相同元素可能被分到不同组，交换后破坏相对位置）

2.5.举例（升序为例）

1）核心动作拆解

核心思路：“分组优化插入排序”

●选基准：每轮排序选择当前数组的最右边元素作为基准值（pivot）。

●分区：将数组分为“小于基准值”“大于等于基准值”两部分，基准值最终放到两部分之间的正确位置。

●递归：对基准值左边的子数组和右边的子数组重复上述步骤，直到子数组长度为 0 或 1。

2）实例分析（[1, 4, 4, 0, 2]）

第 1 轮：处理整个数组 [1, 4, 4, 0, 2]

    ●基准值（pivot）：最右元素 2（index=4）。

    ●目标：将数组分为“小于 2”和“大于等于 2”两部分，最终 2 放到中间。

    ●分区过程（单指针法，记录小于基准的区域边界）：

        初始化 i = -1（i 是“小于基准区域”的右边界，初始为空），j 从 0 遍历到 3（因为基准在 index=4）。

        j=0，元素 1：1 < 2 → 扩大“小于区域”（i++ 变为 0），交换 i 和 j 位置元素（实际相同，数组不变）→ [1, 4, 4, 0, 2]。

        j=1，元素 4：4 ≥ 2 → 不操作，继续遍历。

        j=2，元素 4：4 ≥ 2 → 不操作，继续遍历。

        j=3，元素 0：0 < 2 → 扩大“小于区域”（i++ 变为 1），交换 i=1 和 j=3 位置元素 → [1, 0, 4, 4, 2]。

        遍历结束，将基准值 2 与 i+1 位置元素交换（此时 i=1，i+1=2）→ [1, 0, 2, 4, 4]。

    ●分区结果：

        基准值 2 已放到正确位置（index=2）。

        左子数组（小于 2）：[1, 0]（index 0~1）。

        右子数组（大于等于 2）：[4, 4]（index 3~4）。

第 2 轮：处理左子数组 [1, 0]

    ●基准值（pivot）：最右元素 0（index=1）。

    ●分区过程：

        初始化 i = -1，j 遍历到 0（基准在 index=1）。

        j=0，元素 1：1 ≥ 0 → 不操作。

        遍历结束，将基准值 0 与 i+1=0 位置元素交换 → [0, 1]。

    ●分区结果：

        基准值 0 放到正确位置（index=0）。

        左子数组：空（无需处理）。

        右子数组：[1]（长度 1，无需处理）。

第 3 轮：处理右子数组 [4, 4]

    ●基准值（pivot）：最右元素 4（index=4）。

    ●分区过程：

        初始化 i = 2（当前子数组起始 index=3，i 初始为 2），j 遍历到 3（基准在 index=4）。

        j=3，元素 4：4 ≥ 4 → 不操作。

        遍历结束，将基准值 4 与 i+1=3 位置元素交换（元素相同，数组不变）→ [4, 4]。

    ●分区结果：

        基准值 4 放到正确位置（index=4）。

        左子数组：[4]（长度 1，无需处理）。

        右子数组：空（无需处理）。

最终排序结果：[0, 1, 2, 4, 4]

2.6.代码实现

快速排序的递归实现和非递归实现（用栈和队列模拟递归）。

/// <summary>
/// 快速排序（分治思想，平均效率最优的比较排序）
/// </summary>
/// <param name="arr">待排序数组（会直接修改原数组）</param>
/// <param name="isAscending">排序方向：true=升序，false=降序</param>
/// <param name="isRecursive">是否递归排序</param>
public static void QuickSort<T>(T[] arr, bool isAscending = true, bool isRecursive = false, bool useStack = false) where T : IComparable<T>
{
    if (arr == null || arr.Length <= 1) return;
    if (isRecursive)
        QuickSortRecursive(arr, 0, arr.Length - 1, isAscending);
    else
    {
        if (useStack)
            QuickSortWithStack(arr, isAscending);
        else
            QuickSortWithQueue(arr, isAscending);

    }
}
/// <summary>
/// 递归实现快速排序：分区并递归排序
/// </summary>
/// <param name="arr">待排序数组</param>
/// <param name="left">区间开始索引</param>
/// <param name="right">区间结束索引</param>
/// <param name="isAscending">排序方向：true=升序，false=降序</param>
private static void QuickSortRecursive<T>(T[] arr, int left, int right, bool isAscending) where T : IComparable<T>
{
    //递归终止条件：区间内元素<=1（已序）
    if (left >= right) return;

    //1.分区操作，返回基准元素的最终位置
    int pivotIndex = Partition(arr, left, right, isAscending);

    //2.递归排序基准左侧（小于基准的部分）和右侧（大于基准的部分）
    QuickSortRecursive(arr, left, pivotIndex - 1, isAscending);
    QuickSortRecursive(arr, pivotIndex + 1, right, isAscending);
}
/// <summary>
/// 快速排序分区核心：将数组按基准分为两部分，返回基准最终位置
/// </summary>
/// <param name="arr">待排序数组</param>
/// <param name="left">区间开始索引</param>
/// <param name="right">区间结束索引</param>
/// <param name="isAscending">排序方向：true=升序，false=降序</param>
/// <returns>基准元素在有序数组中的最终索引</returns>
private static int Partition<T>(T[] arr, int left, int right, bool isAscending) where T : IComparable<T>
{
    //选基准
    //方案1：选区间末尾元素作为基准
    //T pivot = arr[right];

    //方案2：选区间中间位置的元素作为基准，优化方案1，"三数取中"避免最坏情况
    int mid = left + (right - left) / 2;//避免(left + right)溢出
    T pivot = arr[mid];
    //将基准元素交换到区间末尾（方便后续遍历）
    (arr[mid], arr[right]) = (arr[right], arr[mid]);

    int i = left - 1;//i：小于基准区域的末尾索引（初始为空，故为left-1）
    //遍历区间[left, right-1]，将元素按基准分组
    for (int j = left; j < right; j++)
    {
        int compareResult = arr[j].CompareTo(pivot);
        bool addToLeft = isAscending ? (compareResult <= 0) : (compareResult >= 0);

        if (addToLeft)
        {
            i++;//扩大小于基准的区域
            (arr[i], arr[j]) = (arr[j], arr[i]);//将当前元素放入小于基准的区域
        }
    }

    //将基准元素交换到"小于基准区域"的末尾（即基准的最终位置）
    i++;
    (arr[i], arr[right]) = (arr[right], arr[i]);

    return i;//返回基准的最终索引
}
/// <summary>
/// 栈实现的非递归快速排序：栈模拟递归，LIFO，避免栈溢出
/// </summary>
/// <typeparam name="T">支持比较的类型（需实现IComparable<T>）</typeparam>
/// <param name="arr">待排序数组（原地排序）</param>
/// <param name="isAscending">排序方向：true=升序，false=降序</param>
public static void QuickSortWithStack<T>(T[] arr, bool isAscending = true) where T : IComparable<T>
{
    int n = arr.Length;
    //用栈存储待排序区间的[left, right]边界（替代递归调用栈）
    //初始压入整个数组的区间：[0, n-1]
    Stack<Tuple<int, int>> stack = new Stack<Tuple<int, int>>();
    stack.Push(Tuple.Create(0, n - 1));

    //栈非空时，持续处理待排序区间
    while (stack.Count > 0)
    {
        //弹出栈顶区间（相当于递归中的当前函数调用）
        var current = stack.Pop();
        int left = current.Item1;
        int right = current.Item2;

        //若区间内元素≤1，无需处理（相当于递归终止条件）
        if (left >= right)
            continue;

        //1.分区操作：获取基准元素的最终位置
        int pivotIndex = Partition(arr, left, right, isAscending);

        //2.将基准左侧和右侧的子区间压入栈（顺序与递归相反，因栈是LIFO）
        //先压入较大的区间，后压入较小的区间（优化：减少栈深度，优先处理小区间）
        if (pivotIndex - left > right - pivotIndex)
        {
            //左侧区间更大，先压入左侧，再压入右侧（弹出时先处理右侧小区间）
            stack.Push(Tuple.Create(left, pivotIndex - 1));
            stack.Push(Tuple.Create(pivotIndex + 1, right));
        }
        else
        {
            //右侧区间更大，先压入右侧，再压入左侧（弹出时先处理左侧小区间）
            stack.Push(Tuple.Create(pivotIndex + 1, right));
            stack.Push(Tuple.Create(left, pivotIndex - 1));
        }
    }
}
/// <summary>
/// 队列实现的非递归快速排序：FIFO特性按顺序处理区间，避免栈溢出
/// </summary>
/// <typeparam name="T">支持比较的类型（需实现IComparable<T>）</typeparam>
/// <param name="arr">待排序数组（原地排序）</param>
/// <param name="isAscending">排序方向：true=升序，false=降序</param>
public static void QuickSortWithQueue<T>(T[] arr, bool isAscending = true) where T : IComparable<T>
{
    int n = arr.Length;
    //用队列存储待排序区间的[left, right]边界（替代递归栈，FIFO顺序处理）
    Queue<Tuple<int, int>> queue = new Queue<Tuple<int, int>>();
    //初始入队整个数组的区间：[0, n-1]
    queue.Enqueue(Tuple.Create(0, n - 1));

    //队列非空时，持续处理待排序区间
    while (queue.Count > 0)
    {
        //出队：取出队首的待处理区间（FIFO，按入队顺序处理）
        var current = queue.Dequeue();
        int left = current.Item1;
        int right = current.Item2;

        //区间内元素≤1时，无需处理（相当于递归终止条件）
        if (left >= right)
            continue;

        //1.分区操作：获取基准元素的最终位置（复用原分区逻辑）
        int pivotIndex = Partition(arr, left, right, isAscending);

        //2.入队：将基准左侧和右侧的子区间加入队列（顺序不影响结果，FIFO会依次处理）
        //先入队左侧区间，再入队右侧区间（也可反过来，最终都会处理）
        queue.Enqueue(Tuple.Create(left, pivotIndex - 1));
        queue.Enqueue(Tuple.Create(pivotIndex + 1, right));
    }
}

其中，Tuple（元组）是C#中的一种固定大小、不可变的数据结构，用于临时存储多个不同类型的元素。可以理解为“一个简单的容器”，专门用来打包少量相关的数据，而无需为这些数据定义一个完整的类或结构体。

3.测试

3.1.完整代码

using System;
using System.Collections.Generic;
using UnityEngine;
using Plugin;

public class SortTest : MonoBehaviour
{
    private void Start()
    {
        int[] arr5 = GenerateArray(10);
        PrintArray(arr5);
        MergeSort(arr5);
        PrintArray(arr5, "归并排序后，数组内容：");

        int[] arr6 = GenerateArray(10);
        PrintArray(arr6);
        QuickSort(arr6);
        PrintArray(arr6, "快速排序后，数组内容：");
    }
    /// <summary>
    /// 生成数组
    /// </summary>
    /// <param name="count"></param>
    /// <param name="minValue"></param>
    /// <param name="maxValue"></param>
    /// <returns></returns>
    private int[] GenerateArray(int count, int minValue = 0, int maxValue = 100)
    {
        List<int> arr = new List<int>();
        for (int i = 0; i < count; i++)
        {
            int value = UnityEngine.Random.Range(minValue, maxValue);
            arr.Add(value);
        }
        return arr.ToArray();
    }
    /// <summary>
    /// 归并排序
    /// </summary>
    /// <param name="arr">待排序数组（会直接修改原数组）</param>
    /// <param name="isAscending">排序方向：true=升序，false=降序</param>
    /// <param name="isRecursive">是否递归实现</param>
    public static void MergeSort<T>(T[] arr, bool isAscending = true, bool isRecursive = false) where T : IComparable<T>
    {
        if (arr == null || arr.Length <= 1) return;
        if (isRecursive)
            MergeSortRecursive(arr, 0, arr.Length - 1, isAscending);
        else
            MergeSortIterative(arr, isAscending);
    }
    /// <summary>
    /// 递归归并排序：二分数组并合并
    /// </summary>
    /// <param name="arr">原数组</param>
    /// <param name="left">当前处理区间左边界</param>
    /// <param name="right">当前处理区间右边界</param>
    /// <param name="isAscending">排序方向：true=升序，false=降序</param>
    private static void MergeSortRecursive<T>(T[] arr, int left, int right, bool isAscending) where T : IComparable<T>
    {
        //递归终止条件：区间内只有1个元素（已序）
        if (left >= right) return;

        //1.二分区间（避免溢出）
        int mid = (left + right) / 2;

        //2.递归排序左半区间和右半区间
        MergeSortRecursive(arr, left, mid, isAscending);
        MergeSortRecursive(arr, mid + 1, right, isAscending);

        //3.合并两个已序子数组
        Merge(arr, left, mid, right, isAscending);
    }
    /// <summary>
    /// 合并两个已序子数组
    /// </summary>
    /// <param name="arr">待排序数组</param>
    /// <param name="left">左子数组开始索引</param>
    /// <param name="mid">左子数组结束索引</param>
    /// <param name="right">右子数组结束索引</param>
    /// <param name="isAscending">排序方向：true=升序，false=降序</param>
    private static void Merge<T>(T[] arr, int left, int mid, int right, bool isAscending) where T : IComparable<T>
    {
        //1.创建临时数组，存储合并结果
        T[] temp = new T[right - left + 1];
        int i = left;//左子数组指针
        int j = mid + 1;//右子数组指针
        int k = 0;//临时数组指针

        //2.按排序方向，依次将两个子数组的小/大元素放入临时数组
        while (i <= mid && j <= right)
        {
            int compareResult = arr[i].CompareTo(arr[j]);
            bool takeLeft = isAscending ? (compareResult <= 0) : (compareResult >= 0);

            if (takeLeft)
            {
                temp[k++] = arr[i++];//取左子数组元素
            }
            else
            {
                temp[k++] = arr[j++];//取右子数组元素
            }
        }

        //3.将左子数组剩余元素复制到临时数组
        while (i <= mid)
        {
            temp[k++] = arr[i++];
        }

        //4.将右子数组剩余元素复制到临时数组
        while (j <= right)
        {
            temp[k++] = arr[j++];
        }

        //5.将临时数组的有序结果复制回原数组的对应区间
        Array.Copy(temp, 0, arr, left, temp.Length);
    }
    /// <summary>
    /// 非递归（迭代）归并排序：原地合并优化，无需递归栈
    /// </summary>
    /// <param name="arr">待排序数组（原地排序，仅需临时数组存储合并结果）</param>
    /// <param name="isAscending">排序方向：true=升序，false=降序</param>
    public static void MergeSortIterative<T>(T[] arr, bool isAscending = true) where T : IComparable<T>
    {
        int n = arr.Length;
        //核心：按“区间步长”迭代合并，步长从1开始（1个元素的区间天然有序）
        //步长每次翻倍（1→2→4→8...），直到步长≥数组长度
        for (int step = 1; step < n; step *= 2)
        {
            //遍历数组，按当前步长划分“相邻两个区间”并合并
            //每次处理两个区间：[left, mid-1] 和 [mid, right]
            for (int left = 0; left < n; left += 2 * step)
            {
                //计算第一个区间的右边界（mid = left + step）
                int mid = left + step;
                //计算第二个区间的右边界（right = left + 2*step -1），避免超出数组长度
                int right = Math.Min(left + 2 * step - 1, n - 1);

                //若mid > right，说明第二个区间为空（只剩一个区间），无需合并
                if (mid > right)
                    continue;

                //合并两个有序区间：[left, mid-1] 和 [mid, right]
                Merge(arr, left, mid - 1, right, isAscending);
            }
        }
    }
    /// <summary>
    /// 快速排序（分治思想实现，平均效率最优的比较排序）
    /// </summary>
    /// <param name="arr">待排序数组（会直接修改原数组）</param>
    /// <param name="isAscending">排序方向：true=升序，false=降序</param>
    /// <param name="isRecursive">是否递归排序</param>
    public static void QuickSort<T>(T[] arr, bool isAscending = true, bool isRecursive = false, bool useStack = false) where T : IComparable<T>
    {
        if (arr == null || arr.Length <= 1) return;
        if (isRecursive)
            QuickSortRecursive(arr, 0, arr.Length - 1, isAscending);
        else
        {
            if (useStack)
                QuickSortWithStack(arr, isAscending);
            else
                QuickSortWithQueue(arr, isAscending);

        }
    }
    /// <summary>
    /// 快速排序递归核心：分区并递归排序
    /// </summary>
    /// <param name="arr">待排序数组</param>
    /// <param name="left">区间开始索引</param>
    /// <param name="right">区间结束索引</param>
    /// <param name="isAscending">排序方向：true=升序，false=降序</param>
    private static void QuickSortRecursive<T>(T[] arr, int left, int right, bool isAscending) where T : IComparable<T>
    {
        //递归终止条件：区间内元素<=1（已序）
        if (left >= right) return;

        //1.分区操作，返回基准元素的最终位置
        int pivotIndex = Partition(arr, left, right, isAscending);

        //2.递归排序基准左侧（小于基准的部分）和右侧（大于基准的部分）
        QuickSortRecursive(arr, left, pivotIndex - 1, isAscending);
        QuickSortRecursive(arr, pivotIndex + 1, right, isAscending);
    }
    /// <summary>
    /// 快速排序分区核心：将数组按基准分为两部分，返回基准最终位置
    /// </summary>
    /// <param name="arr">待排序数组</param>
    /// <param name="left">区间开始索引</param>
    /// <param name="right">区间结束索引</param>
    /// <param name="isAscending">排序方向：true=升序，false=降序</param>
    /// <returns>基准元素在有序数组中的最终索引</returns>
    private static int Partition<T>(T[] arr, int left, int right, bool isAscending) where T : IComparable<T>
    {
        //选基准
        //方案1：选区间末尾元素作为基准
        //T pivot = arr[right];

        //方案2：选区间中间位置的元素作为基准，优化方案1，"三数取中"避免最坏情况
        int mid = left + (right - left) / 2;//避免(left + right)溢出
        T pivot = arr[mid];
        //将基准元素交换到区间末尾（方便后续遍历）
        (arr[mid], arr[right]) = (arr[right], arr[mid]);

        int i = left - 1;//i：小于基准区域的末尾索引（初始为空，故为left-1）
                         //遍历区间[left, right-1]，将元素按基准分组
        for (int j = left; j < right; j++)
        {
            int compareResult = arr[j].CompareTo(pivot);
            bool addToLeft = isAscending ? (compareResult <= 0) : (compareResult >= 0);

            if (addToLeft)
            {
                i++;//扩大小于基准的区域
                (arr[i], arr[j]) = (arr[j], arr[i]);//将当前元素放入小于基准的区域
            }
        }

        //将基准元素交换到"小于基准区域"的末尾（即基准的最终位置）
        i++;
        (arr[i], arr[right]) = (arr[right], arr[i]);

        return i;//返回基准的最终索引
    }
    /// <summary>
    /// 栈实现的非递归快速排序：栈模拟递归，LIFO，避免栈溢出
    /// </summary>
    /// <typeparam name="T">支持比较的类型（需实现IComparable<T>）</typeparam>
    /// <param name="arr">待排序数组（原地排序）</param>
    /// <param name="isAscending">排序方向：true=升序，false=降序</param>
    public static void QuickSortWithStack<T>(T[] arr, bool isAscending = true) where T : IComparable<T>
    {
        int n = arr.Length;
        //用栈存储待排序区间的[left, right]边界（替代递归调用栈）
        //Tuple（元组）是 C# 中的一种固定大小、不可变的数据结构，用于临时存储多个不同类型的元素。可以理解为“一个简单的容器”，专门用来打包少量相关的数据，而无需为这些数据定义一个完整的类或结构体。
        Stack<Tuple<int, int>> stack = new Stack<Tuple<int, int>>();
        //初始压入整个数组的区间：[0, n-1]
        stack.Push(Tuple.Create(0, n - 1));

        //栈非空时，持续处理待排序区间
        while (stack.Count > 0)
        {
            //弹出栈顶区间（相当于递归中的当前函数调用）
            var current = stack.Pop();
            int left = current.Item1;
            int right = current.Item2;

            //若区间内元素≤1，无需处理（相当于递归终止条件）
            if (left >= right)
                continue;

            //1.分区操作：获取基准元素的最终位置
            int pivotIndex = Partition(arr, left, right, isAscending);

            //2.将基准左侧和右侧的子区间压入栈（顺序与递归相反，因栈是LIFO）
            //先压入较大的区间，后压入较小的区间（优化：减少栈深度，优先处理小区间）
            if (pivotIndex - left > right - pivotIndex)
            {
                //左侧区间更大，先压入左侧，再压入右侧（弹出时先处理右侧小区间）
                stack.Push(Tuple.Create(left, pivotIndex - 1));
                stack.Push(Tuple.Create(pivotIndex + 1, right));
            }
            else
            {
                //右侧区间更大，先压入右侧，再压入左侧（弹出时先处理左侧小区间）
                stack.Push(Tuple.Create(pivotIndex + 1, right));
                stack.Push(Tuple.Create(left, pivotIndex - 1));
            }
        }
    }
    /// <summary>
    /// 队列实现的非递归快速排序：FIFO特性按顺序处理区间，避免递归栈溢出
    /// </summary>
    /// <typeparam name="T">支持比较的类型（需实现IComparable<T>）</typeparam>
    /// <param name="arr">待排序数组（原地排序）</param>
    /// <param name="isAscending">排序方向：true=升序，false=降序</param>
    public static void QuickSortWithQueue<T>(T[] arr, bool isAscending = true) where T : IComparable<T>
    {
        int n = arr.Length;
        //用队列存储待排序区间的[left, right]边界（替代递归栈，FIFO顺序处理）
        Queue<Tuple<int, int>> queue = new Queue<Tuple<int, int>>();
        //初始入队整个数组的区间：[0, n-1]
        queue.Enqueue(Tuple.Create(0, n - 1));

        //队列非空时，持续处理待排序区间
        while (queue.Count > 0)
        {
            //出队：取出队首的待处理区间（FIFO，按入队顺序处理）
            var current = queue.Dequeue();
            int left = current.Item1;
            int right = current.Item2;

            //区间内元素≤1时，无需处理（相当于递归终止条件）
            if (left >= right)
                continue;

            //1.分区操作：获取基准元素的最终位置（复用原分区逻辑）
            int pivotIndex = Partition(arr, left, right, isAscending);

            //2.入队：将基准左侧和右侧的子区间加入队列（顺序不影响结果，FIFO会依次处理）
            //先入队左侧区间，再入队右侧区间（也可反过来，最终都会处理）
            queue.Enqueue(Tuple.Create(left, pivotIndex - 1));
            queue.Enqueue(Tuple.Create(pivotIndex + 1, right));
        }
    }
    /// <summary>
    /// 打印数组内容
    /// </summary>
    /// <param name="arr">需打印的数组</param>
    /// <param name="prefix">前缀说明</param>
    public static void PrintArray<T>(T[] arr, string prefix = "数组内容：") where T : IComparable<T>
    {
        if (arr == null)
        {
            Debug.Log($"{prefix} null");
            return;
        }
        Debug.Log($"{prefix} [{string.Join(", ", arr)}]");
    }
}

3.2.测试结果

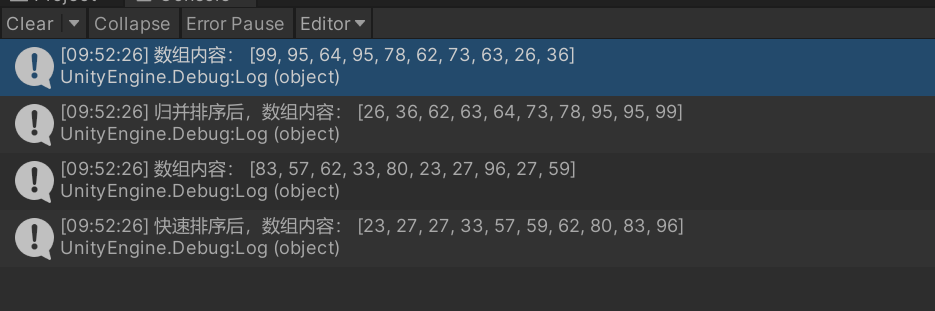
4.总结

插入排序与希尔排序同属“插入类排序”，核心逻辑均基于“将元素插入已排序部分”，均为分治思想下的高效排序算法，平均时间复杂度均为 O(nlogn)，但希尔排序通过“分组插入”优化了插入排序的效率。小数据/有序数据用插入排序（简单、稳定、高效）；中大数据/无序数据用希尔排序（效率高、空间省）。二者共同覆盖了“小规模到中大规模”的排序需求，且都无需额外空间，适合内存有限的场景。

对比维度	归并排序（MergeSort）	快速排序（QuickSort）
核心逻辑	①分（将数组二分至单个元素，默认有序）；②治（将两个有序子数组合并为一个有序数组）；③重复分治（直到合并出原数组长度的有序数组）	①选基准（如选区间中间元素为基准）；②分区（将数组分为"小于/大于等于基准"的两部分）；③递归排序两部分（直至子数组长度为 0 或 1）
时间复杂度	最坏/平均/ 最优：均为 O(n log n)（拆分过程始终将数组分为两半，递归深度固定为 log n，合并过程为 O(n)）	平均/最优：O(n log n)（基准选择合理时，分区后子数组大小均衡，递归深度 log n）；最坏：O(n²)（基准选择极端时，如已排序数组选首尾为基准，子数组一边为空，递归深度 n），可通过“三数取中”选基准优化，降低最坏情况概率。
空间复杂度	递归：O(n + log n)（O(n) 用于合并时的临时数组，O(log n) 为递归调用栈深度）；非递归：O(n)（仅需临时数组，无递归栈消耗）；非原地排序，必须额外申请临时空间。	递归：O(logn)（仅需递归调用栈，用于存储子区间索引，无额外数组）；非递归（迭代）：O(logn)（用栈/队列模拟递归，存储子区间索引）；原地排序，无需额外数组，仅需常数级临时变量。
稳定性	稳定（合并过程中，当左右子数组元素相等时，优先取左侧元素，保留原数组相对顺序）。	不稳定（分区时，基准元素与其他元素交换可能打乱相同值的相对顺序，如 [2, 1, 2] 选右侧 2 为基准，交换后变为 [2, 1, 2] 或 [1, 2, 2]，原两个 2 的顺序改变。
适用场景	1. 需保证稳定排序的场景（如排序含相同值的结构化数据，需保留原顺序）； 2. 数据规模大且内存充足的场景（可接受额外 O(n) 空间）； 3. 链表排序（链表拆分 / 合并无需额外空间，效率高）。	1. 对稳定性无要求的场景（如纯数值排序）； 2. 数据规模大且内存有限的场景（原地排序，空间消耗低）； 3. 平均效率优先的场景（实际工程中，快速排序平均速度比归并排序快 2~3 倍，因缓存友好）。

关键差异分析：

1）分治逻辑：“先分后合”vs“边分边治”

●归并排序的“分”是纯拆分（不涉及元素比较），“治”是核心（合并两个有序数组，需比较元素）；

●快速排序的“分”是核心（分区时通过比较元素确定基准位置，已实现局部有序），“治”是递归分区（无需合并，递归终止即有序）。

简而言之，归并排序是“拆分后靠合并变有序”，快速排序是“分区时直接变有序”。

2）空间消耗：“临时数组”vs“递归栈”

●归并排序的空间消耗来自合并所需的临时数组（必须存储两个子数组的元素才能合并），这是“稳定”和“时间复杂度稳定”的代价；

●快速排序的空间消耗仅来自递归调用栈（存储子区间的 left/right 索引），因无需合并，故可原地排序，空间效率更高。

3）稳定性：“合并逻辑”vs“交换逻辑”

●归并排序的稳定性由“合并规则”保证：相等元素优先取左侧，避免相对顺序改变；

●快速排序的不稳定性由“分区交换”导致：基准元素与右侧小于基准的元素交换时，可能越过中间的相同元素，打乱原顺序（如 [2, 1, 2] 选右侧 2 为基准，交换后变为 [2, 1, 2] 或 [1, 2, 2]，原两个 2 的顺序可能改变）。