控制收缩度量统一机器人轨迹跟踪

使用控制收缩度量统一机器人轨迹跟踪

伊恩·R·曼彻斯特、贾斯汀·Z·唐和让‐雅克·E·斯洛蒂内

1 引言

机器人系统的跟踪控制器设计是一个经典问题，其历史几乎与机器人学本身一样悠久。大多数工业机器人都是全驱动的，即每个构型坐标（自由度）都有一个对应的执行器。此外，许多行走机器人被控制以保持在全驱动状态，即至少有一个平脚牢固地接触地面（参见例如[1]及其中的参考文献）。对于全驱动系统，存在多种普遍适用的跟踪控制方法：使用比例‐积分‐微分（PID）的独立关节控制、计算转矩、滑模控制以及无源性/能量‐based方法等[2, 3]。

对于欠驱动系统，即控制输入少于动力学自由度的系统，情况则大不相同。当前备受关注的许多机器人系统均为欠驱动系统，包括四旋翼飞行器（例如 [4]）、动态行走机器人（例如 [5]）以及带有柔性连杆的轻型机器人（例如 [6]）。已经为欠驱动系统开发了几种非线性控制方法[7, 8],，但目前尚无能够在其最大吸引域内稳定欠驱动系统的通用方法。

一种最近的方法是基于局部线性化设计控制器，例如使用线性二次调节器（LQR）[9],，然后利用计算方法[10]验证吸引域。这些吸引域随后可以被组合起来以扩展控制器的有效性区域[11, 12]。另一种最近的方法利用李雅普诺夫函数的对偶表示来计算最大吸引域的外逼近[13, 14]。

本文中，我们探索了新近提出的“控制收缩度量”（CCM）概念，将其作为经典基于物理的方法与新兴的基于优化的方法在非线性机器人控制中的统一框架。CCM 的思想最初在 [15, 16], 中提出，扩展了 [17] 的分析方法。我们表明，CCM可以被视为统一了上述看似无关的方法。对于全驱动系统，可以选择特定的度量，使得CCM设计恰好退化为滑模与能量基于设计。另一方面，CCM方法在一些关键方面扩展了[10–12]的方法：首先，它生成的控制器能够在某一区域内稳定每一条可行轨迹，而不仅仅是一个必须预先已知的单一目标；其次，控制综合方法可以表示为一个凸优化问题。

条件的凸性带来的好处不仅限于数值优化的易处理性。例如，可以混合搭配不同的规范，如局部最优性和全局稳定性[16]——这为在全局和局部控制器之间切换（例如[18, 19]）提供了一种有趣的替代方案——或者通过组合具有收缩性或极限环行为的运动基元来构建运动[20, 21]。

2 系统描述与问题设定

我们的研究动机源于对一个机械系统的控制，该系统的构型q ∈ Q属于一个n维平滑流形（例如Rn），其动力学由欧拉‐拉格朗日方程导出，并以标准的“操作臂”形式 [2, 3]表示：

$$
H(q)\ddot{q}+ C(q, \dot{q})\dot{q}+ g(q)= Ru. \tag{1}
$$

其中，$H(q)$ 是质量/惯性矩阵，$C(q, \dot{q})\dot{q}$ 包含科里奥利力和离心力项， $g(q)$ 是势场梯度。控制输入为力/力矩 $u \in \mathbb{R}^m$。对于全驱动机器人，$m = n$ 且 $R$ 为满秩方阵；而对于欠驱动机器人，$R$ 为 $n \times m$ 矩阵，且 $m < n$。

回顾可知，(1) 可构造为使得 $H - 2C$ 为斜对称 [2, p. 400]。

我们将在三个经典系统上展示我们的结果：单摆和双摆（均为全驱动）以及欠驱动小车‐倒立摆系统。这些系统的构型坐标和相关参数如图1所示。

就我们的目的而言，通常将动力学方程（1）重写为一个n维的一阶微分方程组会更为方便：

$$
x := \begin{bmatrix} q \ \dot{q} \end{bmatrix}, \quad \dot{x} = f(x) + B(x)u, \tag{2}
$$

其中

$$
f(x) = \begin{bmatrix} \dot{q} \ H(q)^{-1}(-C(q, \dot{q})\dot{q} - g(q)) \end{bmatrix}, \quad B(x) = \begin{bmatrix} 0 \ H(q)^{-1}R \end{bmatrix}. \tag{3}
$$

为了精确定义一个非线性控制问题，我们必须明确所期望的收敛类型。如果构型空间是 $\mathbb{R}^n$，那么 (2) 在 $t \in [0,\infty)$ 上的一个可行解 $x^\ast(t), u^\ast(t)$ 被称为被反馈控制器 $u = k(x,t)$ 全局指数稳定，如果存在正数常数 $K, \lambda$，使得 $|x(t) - x^\ast(t)| \leq K e^{-\lambda t}|x(0) - x^\ast(0)|$ 对所有 $x(0)$ 成立，其中 $x(t)$ 是闭环系统的解。常数 $\lambda$ 被称为收敛速率。对于非线性流形，可以使用适当的距离度量来构造类似的定义。

全局指数稳定性是相对于特定解$x^\ast,u^\ast$定义的。对于机器人跟踪应用，更合适的要求是系统的每一个解都可以被稳定。若存在控制律$u(t)= k(x(t), x^\ast(t), u^\ast(t), t)$，能够以速率 λ全局指数稳定任何可行解$(x^\ast,u^\ast)$，则称系统(2)是普遍指数可稳定的，其稳定速率为 λ。

3 微分动力学与控制收缩度量

黎曼几何将熟悉的欧几里得概念（如距离和角度）扩展到光滑非线性流形 [22]。其核心思想是，在流形的每一点上，通过“度量”在切空间上定义一个局部欧几里得几何：该度量是切向量上的一个平滑变化的内积。在坐标下，这可以写成内积 $\langle \delta_1, \delta_2 \rangle_x = \delta’_1 M(x)\delta_2$，其中正定矩阵$M(x)$随坐标$x$平滑变化。

随后，参数化曲线 $\gamma(s)$，$s \in [0, 1]$的长度可计算为

$$
l(\gamma) = \int_0^1 \sqrt{\langle \gamma_s, \gamma_s \rangle_\gamma} ds
$$

其中 $\gamma_s = \partial\gamma / \partial s$。两点之间的黎曼距离是连接它们的最短路径（“测地线”）的长度。如果流形是 $\mathbb{R}^n$ 且度量 $M$ 与 $x$无关，即“平坦”的，则所有测地线都是直线，且两点之间 $x_1, x_2$的距离仅为 $\sqrt{(x_1 - x_2)’M(x_1 - x_2)}$。

收缩性分析基于动力系统中“邻近”解的相对运动[17]。如果存在某种度量，使得邻近的解之间的距离变小（微分变化缩小），则所有解将全局收敛。这类似于一个显而易见的说法：如果链中的每个环节都变短，则整条链本身必然变短。收缩度量是一种定义在状态空间上的黎曼度量，在系统流的作用下，所有距离都会缩小。

一个光滑非线性系统 $\dot{x}=f(x,t)$沿任意特定解具有微分（即变分、线性化）动力学$\dot{\delta}_x = \frac{\partial f}{\partial x} \delta_x$。收缩性分析的一个关键优势在于，该微分动力学是线性时变的，因此可以将线性系统分析中的许多工具应用于非线性系统，以在无需近似的前提下获得全局结果。

在 [15, 16]这一思想从分析扩展到了控制设计。注意，黎曼度量不仅定义了局部长度测度 $\sqrt{\delta’M(x)\delta}$，还定义了局部正交性概念：在点 $x$ 处的两个切向量 $\delta_1, \delta_2$ 当 $\langle \delta_1, \delta_2 \rangle_x = \delta’_1 M(x)\delta_2 = 0$ 时是正交的。该文的主要结果如下：如果形式为 (2)的控制系统在所有与受控方向正交的方向上都是收缩的，则所有可行轨迹都是可稳定的。这可以被视为经典控制Lyapunov函数概念的一种收缩版本。

为了使表述更精确，我们首先注意到控制系统（2）具有以下动学动态：

$$
\dot{\delta}_x(t) = A(x, u)\delta_x(t) + B(x)\delta_u(t) \tag{4}
$$

其中 $A(x,u) = \frac{\partial f}{\partial x}$。

定理1 ([16]) 考虑系统 (2)及其微分动力学 (4)。如果存在一个对称矩阵函数 $M(x)$和常数 $\alpha_2 \geq \alpha_1 > 0$以及 $\lambda > 0$，使得对所有 $x$ 满足 $\alpha_1 I \leq M \leq \alpha_2 I$，并且对所有 $x, u$ 成立以下蕴含关系：

$$
\delta’_x M B = 0 \Rightarrow \delta’_x(\dot{M} + A’M + M A + 2\lambda M)\delta_x < 0, \tag{5}
$$

那么该系统是普遍指数可稳定的，其稳定速率为 $\lambda$。

该结果也适用于时变系统和度量 [16]。为了理解(5)，考虑微分平方长度 $\delta’_x M(x)\delta_x$的变化率由下式给出

$$
\frac{d}{dt}(\delta’_x M \delta_x) = \delta’_x(\dot{M} + A’M + M A)\delta_x + 2\delta_x M B\delta_u. \tag{6}
$$

根据 $x$、$u$和 $\delta_x$的取值，在(6)中存在两种可能性：如果$\delta’_x MB = 0$，则通过适当选择微分控制输入 $\delta_u$，可使(6)的右侧为负值。实际上，由于(6)对 $\delta_u$是仿射的，因此其负值的幅值可以任意大。

另一方面，如果$\delta’_x MB = 0$，则控制输入对(6)没有影响，但根据(5)，系统是“自然”收缩，即微分长度以速率 $\lambda$减小，因为(5)意味着$\frac{d}{dt} \sqrt{\delta_x’ M(x)\delta_x} < -\lambda \sqrt{\delta_x’ M(x)\delta_x}$。因此可以证明[16]存在一种“微分反馈” $\delta_u(x, \delta_x, u, t)$，它能够稳定微分动力学。

为了构造实际的控制信号 $u$，需要构建一条连接 $x$ 和 $x^\ast$, 的最短路径（测地线）$\gamma$，该路径由 $s \in [0, 1]$ 参数化，即 $\gamma(0)=x^\ast, \gamma(1)=x$，并沿这条平滑路径积分微分控制信号 $\delta_u$：

$$
u(t, s) = u^\ast(t) + \int_0^s \delta_u\left(\gamma(s), \frac{\partial\gamma}{\partial s}(s), u(t, s)\right) ds, \tag{7}
$$

而实际应用的控制信号是$u(t) = u(t,1)$，详见[16]中的细节与证明。通常情况下，这涉及一种在线优化，类似于（但比）模型预测控制更简单的方法，以求解 $\gamma$。然而，如上所述，如果度量与$x$无关，则测地线就是直线。

3.1 通过凸优化求解

CCM方法的一个显著优势是，与控制Lyapunov函数不同，寻找CCM可以被表述为一个凸优化问题。

变量替换 $\eta = M(x)\delta$和 $W(x) = M(x)^{-1}$后，(5) 可重写为$\dot{\eta}’B$意味着 $= 0$

$$
\eta’(-\dot{W} + AW + WA’ + 2\lambda W)\eta < 0.
$$

这可以表示为简化形式：

$$
B’ \perp(- \dot{W} + A W + WA’ + 2\lambda W)B \perp < 0, \tag{8}
$$

其中 $B_\perp(x)$是满足对所有 $x$ 成立 $B_\perp(x)’B(x) = 0$ 的矩阵函数。在张量分析中，矩阵 $W$是一个 对偶 度量（逆变而非协变），而双射 $\delta \leftrightarrow \eta$ 与“音乐同构”相关。

约束条件（8）以及 $W(x)$的一致有界性在 $W(x)$ 的元素上均为凸的。两者均可表示为逐点线性矩阵不等式（LMI），并推广了线性时不变系统可镇定性的标准 LMI 条件 [23]。尽管是凸的，这些条件却是无限维的：因为 $W$的元素是 $x$ 的平滑函数，且存在无穷多个约束：LMI 条件必须对所有 $x$ 成立。

为了进行数值求解，我们需要一个有限维近似。标准方法包括选择某些函数基（例如多项式或三角多项式），然后通过对状态空间的一个区域进行网格化来施加约束，或者使用对正多项式集合的可处理（例如 LMI）近似，如平方和或相关近似 [10, 12]。平方和方法在 [24] 中已被用于收缩 分析。

一个更明确的条件如下：

$$
- \dot{W} + A W + WA’ - \rho BB’ + 2\lambda W \leq 0. \tag{9}
$$

这个条件显然蕴含了(8)，因为分别左乘和右乘 $B’ \perp$ 和 $B \perp$ 后，涉及 $\rho$ 的项消失。此外，这导致了一个显式构造的微分控制 $\delta_u = -K(x)\delta_x$，其中 $K = -\frac{1}{2\rho}B’W^{-1}$。注意，如果度量 $\rho$ 和 $B$与 $x$ 无关，则所得的控制律只是一个线性反馈增益：

$$
u(t) = u^\ast(t) - \frac{1}{2\rho}B’W^{-1}(x(t) - x^\ast(t)).
$$

4 全驱动机器人的CCM设计

CCM 的条件可以表示为一个凸优化问题。然而，为了理解该方法，考虑可以解析构造 CCM 的情况是很有意义的。在本节中，我们表明前一节中的 CCM 条件对于“二阶”且全驱动的系统会简化为一种非常简单的形式。此外，所得的设计结果与滑模控制密切相关。

式(2)、(3)的微分动力学形式为：

$$
\frac{d}{dt}\begin{bmatrix}\delta_1\\delta_2\end{bmatrix} = \underbrace{\begin{bmatrix}0 & I \ \cdot & \cdot\end{bmatrix}} {A(x)} \begin{bmatrix}\delta_1\\delta_2\end{bmatrix} + \underbrace{\begin{bmatrix} 0 \ H(q)^{-1}R\end{bmatrix}} {B(x)} \begin{bmatrix}\delta_1\\delta_2\end{bmatrix}
$$

其中 $\cdot$ 表示一个不会影响本节结果的元素。对于 $B(x)$，我们唯一需要的信息是 $H(q)^{-1}R$为满秩，这对于全驱动系统是成立的。

考虑该系统的对偶‐CCM条件（8）。零化矩阵$B_\perp(x)$可以是任意满足 $B_\perp(x)’B(x) = 0$ 的矩阵，因此它不是唯一确定的，但一个简单且自然的选择是 $B_\perp = [I\ 0]’$。

一般来说，我们可以选择一个状态相关的度量$M(x)$或对偶度量$W(x)=M(x)^{-1}$，但对于这类系统而言，考虑常值度量已足够，我们将该常值度量分解为四个$n \times n$块：

$$
W = \begin{bmatrix}W_{11} & W_{12} \ W’ {12} & W {22}\end{bmatrix}.
$$

条件（8）简单表明，若$W$的左上块矩阵在$AW + WA’ + 2\lambda W$中为负定，则 $W$是双CCM。但由于$A(x)$结构简单，这可简化为如下表述

$$
W_{12} + W’ {12} < -2\lambda W {11}. \tag{10}
$$

换句话说，任何具有对称部分为负定的非对角块的正定分块矩阵都是某个 $\lambda > 0$的对偶‐CCM。这对于任意二阶全驱动系统都成立，而与动力学无关。

让我们考察该陈述对于一个具有状态$q, \dot{q}$的单自由度系统的几何意义。此时$W$是一个$2\times2$矩阵。由于要求$W_{11}$为正，条件$W_{12} + W’ {12} < -2\lambda W {11}$意味着$W_{12}$为负。根据$2\times2$矩阵的逆矩阵公式，度量$M = W^{-1}$的所有元素必须为正。

现在，由于 $B = [0, 1]’$，未受控的微分（即满足 $\delta_x’MB = 0$） $\dot{}$ 必须满足 $\delta_q m_{12} + \delta_{\dot{q}} m_{22} = 0$，即 $\delta_{\dot{q}} = -\frac{m_{12}}{m_{22}} \delta_q$。但由于 $M$ 的所有元素均为正数，任何非零的 $\delta_q$ 和 $\delta_{\dot{q}}$ 符号相反，即坐标微分 $\delta_q$ 的长度正在收缩。同时，条件 $\delta_x’MB = 0$ 表明，存在于微分动力学第二行中的加速度微分对平方长度 $\delta_x’M\delta_x$没有影响。

4.1 与滑模控制的联系

我们已经证明，对于二阶全驱动系统，构造平坦控制收缩度量是容易的。有趣的是，当取特定极限时，这种构造会过渡到另一种保证二阶系统收敛的方法：滑模控制。在滑模控制中，人们为构型坐标选择某种期望的一阶动力学，例如

$$
\frac{d}{dt}(q(t) - q^\ast(t)) = -a(q(t) - q^\ast(t)) \tag{11}
$$

对于某个常数 $a > 0$。对于二阶系统，这意味着状态应迅速移动到相空间中由 $\frac{d}{dt}(q - q^\ast) + a(q - q^\ast) = 0$给出的直线，该直线被称为“滑动面”。该目标可以通过施加高增益或切换力反馈来实现，以驱动关节速度趋近于 $\dot{q}^\ast (t) - a(q(t) - q^\ast (t))$。

让我们构造对偶‐CCM $W$，使其具有如下形式

$$
W = \begin{bmatrix} I & -\lambda I \ -\lambda I & (1+ \varepsilon)\lambda^2 I\end{bmatrix},
$$

其中 $\varepsilon$和 $\lambda$为正数常数。根据构造，该$W$满足（10），并且是正定的，因为对右上角分块取舒尔补得到$(1+ \varepsilon)\lambda^2 I - \lambda^2 I = \varepsilon\lambda^2 I$，其为正定矩阵。

进行分块矩阵求逆，并令$a = \frac{1}{\lambda}$，可得度量$M = W^{-1}$：

$$
M = \begin{bmatrix}(1+ \frac{1}{\varepsilon})I & \frac{1}{\lambda\varepsilon}I \ \frac{1}{\lambda\varepsilon}I & \frac{1}{\lambda^2 \varepsilon} I\end{bmatrix} \approx \frac{1}{\varepsilon}\begin{bmatrix} I & aI \ aI & a^2 I\end{bmatrix} = \hat{M}
$$

其中近似 $M \approx \hat{M}$ 在 $\varepsilon \ll 1$ 时成立。现在，$\hat{M}$ 的特征值/特征向量对具有如下形式：

$$
\lambda_i = 0, v_i = \begin{bmatrix}a e_i \ -e_i\end{bmatrix}, \lambda_{n+i} = \frac{1}{\varepsilon}(1+ a^2), v_2 = \begin{bmatrix} e_i \ a e_i\end{bmatrix}, i = 1, 2,…, n, \tag{12}
$$

其中$e_i$是除第$i$th个分量为1外其余元素均为零的向量。因此，当 $\varepsilon \to 0$时，度量的等值集在$v_1,$方向上趋近于长谷形状，并在$v_2$方向上具有非常陡峭的侧壁。

一个使$\delta_x’M\delta_x$呈指数衰减的反馈控制器必然会使沿$v_2$方向的状态偏差迅速缩小，但并不需要使沿$v_1$方向的偏差缩小。因此，在短暂的瞬态过程后，微分将几乎落在直线$a\delta_q + \delta_{\dot{q}} = 0$上。如果所有微分都如此对齐，则 $\dot{q} - \dot{q}^\ast = -a(q - q^\ast)$，这正是上述滑模控制器所描述的目标动力学。

4.2 示例：倒立摆

单摆提供了一个有用的示例，因为所有细节都可以手动推导出来，并能完整绘制结果。系统的状态空间是柱面的，这使我们能够阐明基于测地线的控制律的几何和物理意义。归一化物理参数后，我们可以将摆的动力学写为

$$
\ddot{q} + d \dot{q} + \sin q = u.
$$

在状态空间 $x=[q, \dot{q}]’$上，我们得到微分动力学（4），其中

$$
A(x) = \begin{bmatrix} 0 & 1 \ -\cos q & -d\end{bmatrix}, \quad B = \begin{bmatrix}0\1\end{bmatrix}.
$$

对于该系统，$W$是一个 $2 \times 2$矩阵，且条件(10)简化为$w_{12} < -\lambda w_{1}$。因此，任何具有负非对角元素的正定矩阵都是简单摆的对偶‐CCM。通过取逆，任何具有正非对角元素的常数正定矩阵都是简单摆的CCM。

让我们采用特定的度量 $m_{11} = 5, m_{12} = 2, m_{22} = 1$，并考虑上摆至直立位置的问题。图2表示将柱面相空间“展开”到 $\mathbb{R}^2$上的情况。该图描绘了开环相图，其中两个平衡点周期性重复出现。同时，图中还描绘了到目标（直立）平衡点的黎曼距离的等值集。注意，在这个展开的状态空间中存在某些对角“带状区域”：每个这样的带中的所有状态都共享某个特定的关于目标平衡点的展开方式作为其最近的。在黎曼几何中，这些带之间的分界线称为 割迹 [22,第 13]章。

带状区域的形状可以解释如下：当 $\theta$为正时，系统在相图中向右移动，因此从度量的角度来看，右侧的目标平衡点会显得“更近”。例如，在闭环控制下，若初始 $\theta$非常大，则摆锤会在停止前旋转数圈。

到目前为止，我们有了度量但还没有控制增益，因此我们应用更具构造性的条件（9）

$$
\begin{bmatrix}2(w_{12} + \lambda w_1) & w_2 - w_1 \cos q - w_{12}d + 2\lambda w_{12} \ \cdot & 2(\lambda w_2 - w_{12} \cos q - w_2 d) - \rho(x)\end{bmatrix} \leq 0.
$$

假设$w_{12} < -\lambda w_1,$，这通过舒尔补等价于以下陈述

$$
\rho(x) \geq \frac{(w_2 - w_1 \cos q - w_{12}d + 2\lambda w_{12})^2}{2(w_{12} + \lambda w_1)} - 2(\lambda w_2 - w_{12} \cos q - w_2 d),
$$

可以通过 $\rho(x)$ 逐点施加该条件。为了实现更激进的控制，可以采用固定增益反馈：由于 $w_1, w_2 > 0$ 且 $w_{12} < 0$ 右侧在 $\cos(x) = -1$ 时取得最大值，即 $x = \pi \pm 2k\pi, k = 1, 2, 3,…$。因此，取常数乘子即可：

$$
\rho = \frac{(w_2 + w_1 - w_{12}d + 2\lambda w_{12})^2}{2(w_{12} + \lambda w_1)} - 2(\lambda w_2 + w_{12} - w_2 d)
$$

以及常系数线性反馈 $u = -\frac{1}{2} \rho B’ W^{-1} (x - x^\ast)$。

图3显示了割迹两侧两个邻近初始条件的闭环响应。注意，在展开表示中，它们收敛到不同的平衡点，而在（真实的）柱面相空间中，它们都收敛到直立平衡点，但绕圆柱体的缠绕次数不同。

5 基于能量的控制和虚拟系统

上一节的设计仅使用了非常有限的物理知识：第二组状态变量是第一组状态变量的导数。在本节中，我们展示了一种基于所谓“虚拟控制系统”的替代方法，该方法利用了更多的物理信息，并产生了一个经典的基于能量的跟踪控制器。我们还将展示如何将这些设计应用于为非线性流形上的系统指定期望的动力学。

虚拟系统[25, 26]中被引入用于收敛性分析，这里我们将该技术扩展到控制设计。对于给定系统（2），一个虚拟系统是一种形式为的新系统

$$
\dot{y} = \bar{f}(y, x) + \bar{B}(y, x)u \tag{13}
$$

具有如下性质：$\bar{f}(x,x) = f(x)$且$\bar{B}(x,x) = B(x)$，其中 $y, x \in \mathbb{R}^n$。变量$x$作为外生输入，是真实系统(2)的状态。

定理2 假设对于(5)中的虚拟系统，即关于 $y$ 的微分，存在某个度量 $M(y, x,t)$成立，则对于 $x^\ast (t)$的任意轨迹(2)，若存在控制律 $\bar{u}(x,x^\ast)$，使得

$$
\dot{x}^\ast = \bar{f}(x^\ast, x) + \bar{B}(x^\ast, x)\bar{u}(x, x^\ast), \tag{14}
$$

对于所有 $x, t$ 可以被全局指数稳定。

证明 针对虚拟系统，使用[15]的方法构造一个控制器，将真实状态$x$视为时间变化，除了在（7）中，以 $\bar{u}$（t）替代$u^\ast$（t）作为边界条件。根据构造方式，存在一条虚拟系统的状态路径系统 $\gamma$的长度呈指数级收缩。此外，使用 $\bar{u}(t)$作为边界条件，确保该路径的一端（$s = 0$）遵循真实系统的期望轨迹$x^\ast(t)$，而另一端（$s = 1$）遵循真实系统的实际轨迹$x(t)$，这是基于$f(x, x) = f(x)$和$B(x, x) = B(x)$的性质。因此，$x$与$x^\ast$之间的距离呈指数级减小。需要注意的是，中间轨迹$s \in (0,1)$不一定对应真实系统的轨迹。□

机械系统是虚拟系统可以简化控制设计的一个重要示例。对于系统（1），我们可以构造相关的虚拟系统（类似于 [26]）：

$$
H(q)\dot{y} + C(q, \dot{q})y + g(q) = Ru
$$

其中 $(q, \dot{q})$ 是真实状态。由于系统是全驱动的，不失一般性地假设 $R = I$，这总可以通过对控制输入进行变量变换来实现。注意虚拟系统在 $y$ 中是线性的。虚拟系统的微分动力学由 $H(q)\delta\dot{y} + C(q, \dot{q})\delta y = \delta u$ 给出。现在考虑度量 $\delta’_y H(q)\delta y$。其导数为 $\frac{d}{dt}(\delta’_y H(q)\delta y) = \delta’_y(\dot{H} - 2C)\delta y + 2\delta’_y \delta u = 2\delta’_y \delta u$。第二个等式源于 $H - 2C$ 的斜对称性。因此，任何形式为 $\delta u = -K(q)\delta y$ 且 $K(q)$ 正定的微分反馈都能稳定该微分动力学。由于度量 $H(q)$ 和增益 $K(q)$ 与 $y$ 无关，测地线为直线，反馈控制器的形式为 $u = \bar{u} - K(q)(\dot{q} - \dot{q}^\ast)$ 且

$$
\bar{u} = H(q)\ddot{q}^\ast + C(q, \dot{q})\dot{q}^\ast + g(q).
$$

该控制器将使广义速度稳定至 $\dot{q}^\ast$。然后可以使用 $\dot{q}^\ast$ 来设计期望的一阶动力学，如滑模控制 [27]。

5.1 示例：双摆的上摆

我们将通过将上述方法应用于（全驱动）双摆的上摆控制来说明该方法。构型空间在拓扑上是环面的：$q = [\theta_1, \theta_2]’$，其中 $\theta_1$为“肩部”连杆相对于向下位置的角度，$\theta_2$为“肘部”角度。运动方程可参见例如[3, 8]。

滑动面的一个常见选择是(11)，但另一种尊重相差 $2\pi$角度的恒等性的选择是 $\frac{d}{dt}(\theta - \theta_d) = -\lambda \sin(\theta - \theta_d)$，其中 $\theta_d$是某个期望角度。该方法为每个坐标分配了平滑且几乎全局稳定的动力学。注意，这涉及减去位于流形不同点上的速度，其结果依赖于特定的坐标系选择。对于非线性流形上的系统，一种替代方法是将向量传输方法融入[28]中。

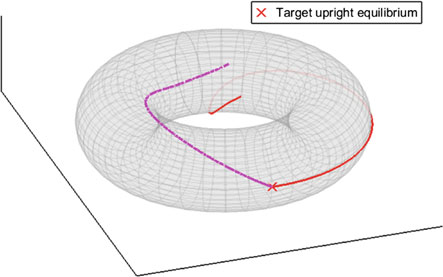
仿真的结果如图4所示，以展开坐标表示。与之前一样，来自两个相近初始条件的闭环轨迹分离，并收敛到明显不同的平衡点。在图5中，构型轨迹被绘制在环面上，可以清楚地看到两者都收敛到同一个平衡点（两个摆均处于竖直向上位置），但在环面上具有不同的环绕次数。

6 欠驱动机器人与基于优化的综合

对于欠驱动系统（即执行器数量少于自由度的系统），第4和5节中的技术不能保证适用。另一种最近提出的方法是使用线性最优控制技术（例如 LQR）对系统进行局部稳定化，然后通过半代数优化验证某一区域内的稳定性[10–12]。在本节中，我们讨论 CCM 与这些基于优化的方法之间的联系。

考虑以下用于跟踪期望轨迹$x^\ast(t),u^\ast(t),t \in [0,\infty)$的类LQR成本函数族：

$$
J(x, u) = \int_0^\infty [(x - x^\ast)’ Q(x - x^\ast) + (u - u^\ast)’R(u - u^\ast)]dt.
$$

假设存在一个一致正定矩阵 $W(x)$，使得

$$
\begin{bmatrix} (\dot{W} - WA’ - AW + BR^{-1}B’) & WL’ \ L W & I \end{bmatrix} \geq 0, \tag{15}
$$

对于所有$x, u$，其中$Q = L’L$，则对于任意目标轨迹和任意初始条件$x(0)$，CCM控制器在成本上实现了以下上界：$J(x, u) \leq d_M(x(0),x^\ast(0))^2$，其中$d_M$是由$M = W^{-1}$诱导的黎曼距离。

注意，如果 $W$、$B$为常数，且(15)在平衡状态处取值，则通过舒尔补，它等价于条件 $WA’ + AW - BR^{-1}B’ + W QW \leq 0$。在两侧同时乘以 $M = W^{-1}$并将不等式替换为等式，即可得到LQR控制的代数Riccati方程 [9]。由此可见，若系统在某一平衡点处局部指数稳定，则在该点周围的某个区域内存在CCM。

6.1 与LQR-Trees和模型预测控制的关系

让我们将这种方法与LQR‐Trees [11]进行关联。通过使用CCM，可以选择状态空间中的某个区域X，然后寻找在所有$x \in X$上有效的CCM是一个凸的（尽管是无限维的）问题。实际上，该问题可以通过网格化或结合拉格朗日乘子的平方和方法求解。在LQR‐Trees中，使用LQR找到一个局部有效的控制器，然后利用平方和方法估计其有效性区域。此外，[11]的方法构造的控制器仅稳定某个特定的目标平衡点或目标轨迹，而CCM方法产生的控制器能够在无需目标轨迹先验知识的情况下，稳定任何保持在已验证区域内的可行轨迹。

此外，CCM 方法可以被视为 LQR（或其他基于线性化的方法）与模型预测控制之间的一种“折中方案”：前者具有凸的离线综合和廉价的在线计算，但稳定性是局部的；而后者原则上具有全局稳定性，但在线计算可能难以承受。在 CCM 方法中，需要通过一个离线凸问题来寻找 CCM，然后通过在线测地线优化来计算实时控制器，由于没有动态约束，在线测地线优化比 MPC 更简单。这一关系在 [29] 中得到了详细探讨。

6.2 示例：欠驱动小车-倒立摆系统

小车‐倒立摆系统是欠驱动系统的一个经典示例：一个无驱动的倒立摆安装在一个驱动小车上。系统有两个构型坐标：摆杆角度 $\theta$和小车位置 $\xi$。其导数分别记为$\omega$和 $v$，控制输入是作用于小车的力，$u$。见图1。

为简化计算，我们首先对[30]应用部分反馈线性化，得到状态向量 $[\theta, \omega, \xi, v]’$，其动力学为$\dot{\theta} = \omega, \dot{\omega} = \sin(\theta) - \cos(\theta)u, \dot{\xi} = v, \dot{v} = u$。如第 3节所述，若$B$、$W$和 $\rho$与$x$无关，则CCM控制器是线性的。基于此考虑，我们采用新坐标$x = [\theta, \eta, \xi, v]’$，其中 $\eta = \sec \theta \omega$，该变换在$\theta \in (-\pi/2, \pi/2)$上是一个可逆变换。在此坐标系下，系统的动力学为

$$
\frac{d}{dt} \begin{bmatrix} \theta \ \eta \ \xi \ v \end{bmatrix} = \begin{bmatrix} \eta \cos\theta \ \eta^2 \sin \theta + \tan \theta \ v \ 0 \end{bmatrix} + \begin{bmatrix} 0 \ -1 \ 0 \ 1 \end{bmatrix} u,
$$

以及微分动力学为：

$$
\dot{\delta} x = \underbrace{\begin{bmatrix} -\eta \sin \theta & \cos\theta & 0 & 0 \ -\eta^2 \cos\theta + \sec^2 \theta & 2\eta \sin \theta & 0 & 0 \ 0 & 0 & 0 & 1 \ 0 & 0 & 0 & 0 \end{bmatrix}} {A(x)} \delta_x + \underbrace{\begin{bmatrix} 0 \ -1 \ 0 \ 1 \end{bmatrix}}_{B} \delta_u.
$$

请注意，这些变换仅用于简化计算：已在[16]中证明，CCM 的存在性在变量的光滑变换和仿射反馈变换下保持不变。

对于该系统，我们使用了LMI解析器Yalmip [31]和求解器Mosek来求解$W$以满足(15)，成本权重为 $Q = \text{diag}[1, 1, 15, 1]$和 $R = 10$，在区域 $\theta \in [-\pi/4,\pi/4]$和 $\eta \in [-0.5,0.5]$进行网格化。该优化问题在标准台式计算机上求解耗时约1.6秒。

跟踪结果如图6所示。系统首先响应初始条件$x = [0.2,0,-0.1, 0]’$，且期望状态在原点（即保持直立平衡）。20秒后，期望小车位置发生阶跃变化 $\xi^\ast = 0.15$，其他所有期望状态保持为零。控制器响应以将小车带到新的期望位置。40秒后，期望小车位置线性地回到原点，且期望小车速度相应设置。经过短暂瞬态，受控系统收敛到该路径。

请注意，在所有这些仿真中，期望的摆锤位置保持竖直： $\theta^\ast = 0$。因此，参考轨迹对于非线性系统实际上是不可行的，因为如果小车加速，未驱动的摆锤将无法保持竖直。

7 结论

我们探讨了使用控制收缩度量（CCM）来设计机器人轨迹跟踪控制器的方法。本文的核心思想是，一方面，CCM将线性化/基于优化的方法（例如 LQR‐Trees）扩展到了跟踪问题，并且可以通过凸优化来求解；另一方面，对于全驱动系统，CCM条件可以解析求解，并退化为经典的滑模和基于能量的设计方法。因此，CCM可被视为连接此前相互分离的各类方法的桥梁。