多天线索引编码联合设计

基于多天线空间复用的无线索引编码传输

摘要

索引编码，即编码多播，是一种通过利用用户内存中存储的数据来减少传输次数的有前景的传输方案。在多天线情况下，索引编码增益可以通过空间复用来进一步提升，但现有文献尚未充分解决索引码与波束成形的联合设计问题。本文通过联合设计多播波束成形器和索引码，研究了空间复用索引码的增益。由于最优联合设计问题本身是NP难的，我们采用两步法：第一步，针对任意索引码，设计基于共轭梯度的多组多播波束成形；第二步，选择使总传输时间最小的索引码。我们的仿真结果显示，所提出的方案在空间复用索引码上表现出显著增益。

一、引言

预计到 2026[1],，无线数据流量的需求将激增至前所未有的120艾字节，因此，在无线资源有限的情况下应对无线数据流量的爆炸式增长至关重要。多播传输通过同时向多个请求相同数据的用户发送相同的数据，是应对无线流量激增的一种高效方式。近年来，索引编码（又称编码多播）利用用户端存储信息，通过异或操作同时满足多个用户请求，为多播传输带来了新的思路。由于用户设备具备大容量内存且成本较低，索引编码已成为减少无线数据流量的一项颇具前景的技术。

在[2]中研究了广播信道在各种方案下的速率区域；特别是在双用户情况下，[2]的作者表明不同的方案（例如，简单的时分复用和叠加编码）提供了不同的外边界。此外，[3]的作者表明，通过应用网络编码可以扩展广播擦除信道的可达速率区域，而[4]的作者表明，在考虑异或操作的软信息的情况下，广播瑞利衰落信道下也可实现进一步的扩展。由于索引编码可被解释为一种信源编码中，文献中的索引码设计通常与传输方案分开进行，并且没有充分考虑信道衰落[5],[6]等信道条件。在这种解耦设计中，最优索引码简单地变为最短的索引码，且不随信道条件变化。与这种广泛应用的方法相反，论文[7]最近揭示了最优索引码依赖于信道条件，且在索引码设计中考虑信道效应至关重要。然而，[7]的结果无法直接应用于或扩展到多天线设置。鉴于寻找最优索引码通常是NP难[8], ，设计空间复用索引码更加复杂。

由于上述障碍，尽管在多篇论文[9]–[11],中已对多输入单输出广播信道（MISO BC）中的索引编码进行了研究，但在索引码与波束成形的联合设计方面仍存在较大局限。当使用预定义的索引码并结合零强迫（ZF）波束成形时，[9]的作者探索了速率分割，以实现可随用户数量扩展的内容分发。在[10],中，研究了空时编码与零迫波束成形相结合，在多个时隙上传输给定索引码的传输方案。在[10],结果的基础上，[11]的作者进一步考虑了多组多播场景。这些论文均侧重于与索引码设计解耦的波束成形设计。

在本文中，我们尝试研究空间复用索引码在MISO广播信道中的增益。该结果首次将[7]中的观察结果扩展到多天线场景，并推动了波束成形器与索引码的联合设计。具体而言，对于任意索引码，我们首先利用共轭梯度法获得多组多播波束成形器。然后，我们在用户给定存储状态的所有可能的团覆盖索引码中识别出可解码索引码。最后，我们在这些可解码索引码中选择最优解，使其与相应的波束成形器配合时总传输时间最小。我们的仿真结果表明，所提出的方案在所有信噪比区域均减少了传输时间，揭示了空间复用索引码的巨大增益。

II. 问题建模

A. 系统模型

我们考虑一种每个用户都带有缓存的多输入单输出广播信道（MISO BC）。具有 N _t 根天线的发射机为 K个用户服务，每个用户配备单天线。发射机拥有一个包含 N(≥ K)个文件的文件库，且每个文件也可以被解释为一个数据包，用于传递所请求的信息。

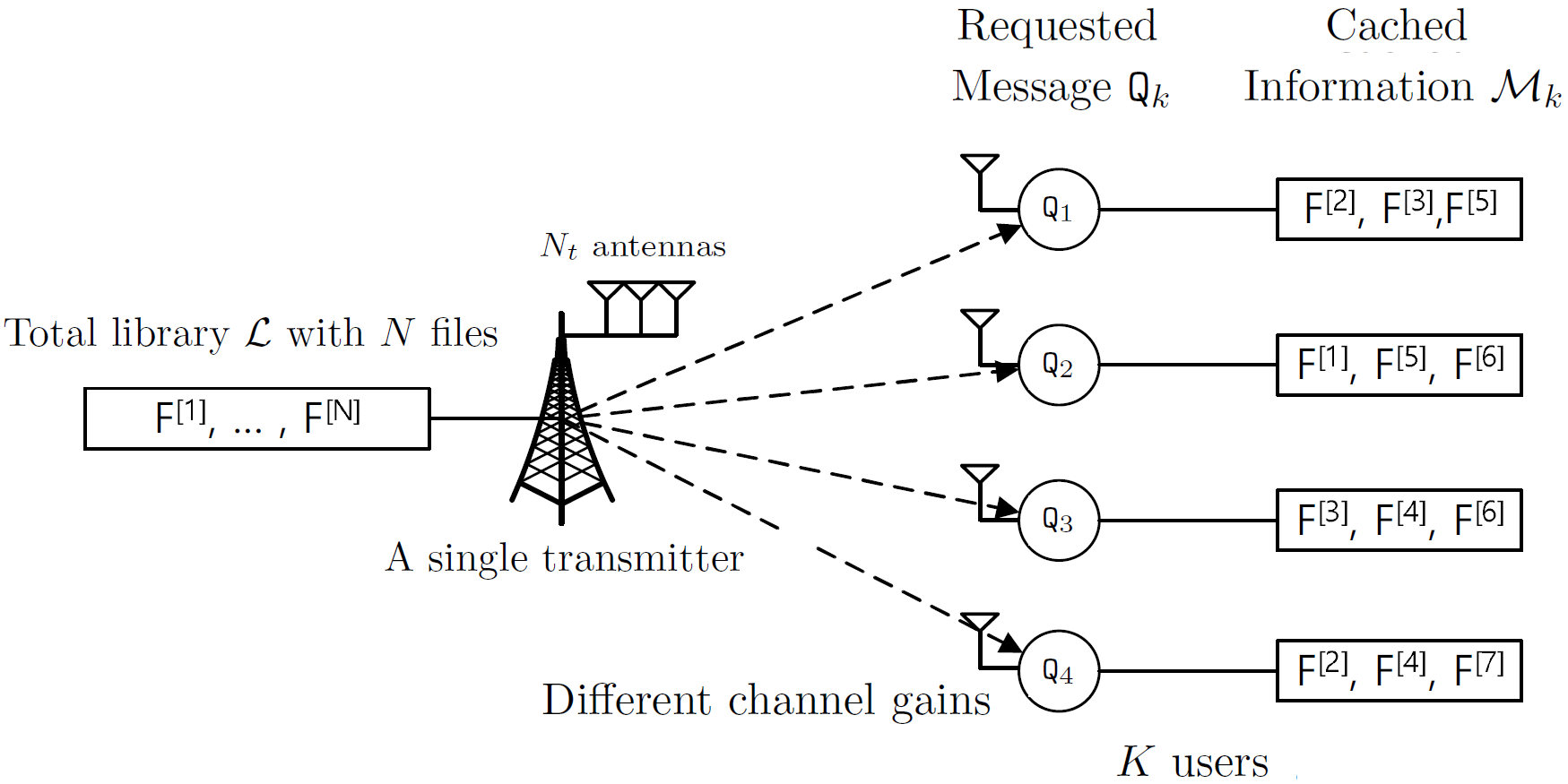
用户从文件库中请求一个文件。同时，每个用户都有一个内存，其中存储了 M个除请求的文件之外的文件。发射机处的文件库表示为L,{F[1],…, F[N]}，其中F[n]是第 n个文件，其大小为B比特。我们还用Q _k ∈ L表示用户 k请求的文件，M _k ⊂ L{Q _k }表示存储在用户 k内存中的文件集合，其中\是集合差运算符。此外，我们假设各用户的请求文件互不相同，即当 i ≠ j时，Q _i ≠ Q _j 。发射机知晓每个用户的内存状态（即已保存的文件），因此能够利用已保存的文件构造多种索引码。

在MISO广播信道中，用户 k的接收信号，记为y _k ∈ C，被建模为
y _k = h ^† _k x+ z _k ,
其中，h _k ∈ C ^{N _t ×1} 是用户 k 的信道向量，其元素为零均值和单位方差的复高斯随机变量，即 h _k ∼ CN(0, 1 _{N t} )，而 (·) ^† 表示向量的共轭转置。我们考虑慢衰落信道模型，因此信道系数h _k 在单次传输周期内保持不变，但在多次传输之间发生变化。发射机精确已知用户的信道，即 {h ₁ ,…, h _K }，这在慢衰落信道中相对容易实现。此外，z _k ∈ C 是零均值和单位方差的复高斯噪声，即 z _k ∼ CN (0, 1)。

在本文中，我们考虑所有用户通过多天线空间复用同时被服务。传输包含两个组成部分：1）索引码和2）波束成形向量。对所有 K用户的传输最多需要 K个不同的流 （即，波束），因此我们可以用K个互不相交的用户组来表示任意团覆盖索引码，每个用户组对应一个流。设 G ₁ , …, G _K ⊂[K]为 K个用户组，其中 G _i 是在第 i个流中一起服务的用户组，满足[K],{1, · · ·, K}且 G ₁ ∪…∪G _K =[K]。那么，用户组 G _i 的消息由该组中所有用户请求的消息进行异或操作构造而成。因此，针对 K 个用户的索引编码设计等价于将用户划分为 K个用户组。

设 I(·)为组索引指示器，其接收用户索引并返回该用户所属的组索引，即 I(k)=i ←→ k ∈ G _i 。然后，发送信号x ∈ C ^{N _t ×1} 按如下方式构造：
x, ∑ ^K _i=1 v _i m _i , (1)
其中 m _i 是第 i 个调制消息（即发送给用户组 G _i 的消息），满足 E[‖m _i ‖ ² ]= 1，且 v _i ∈ C ^{N _t ×1} 是用户组 G _i 的波束成形器，满足
‖v ₁ ‖ ² + · · ·+ ‖v _K ‖ ² ≤ P
在总发射功率预算 P下。由于调制消息 m ₁ ，…， m _K 彼此独立，我们有E[‖x‖ ² ] ≤ P.。注意，如果某些用户被同时服务，则存在空组，此时我们不对相应的波束分配功率，即当 G _i = ∅时， ‖v _i ‖ ² = 0。

B. 问题描述

对于给定的索引码 G _1:K (, G ₁ ,…, G _K )，发射机将总传输功率 P分配给 K个不同的数据流（或 K个波束成形向量），以最小化总传输时间。注意，总传输时间与服务质量相关，这在视频流等无线内容分发网络中非常重要。

用户 k的接收信号变为
y _k = h ^† _k v _I(k) m _I(k) + h ^† _k ( ∑ _{i∈[K]{I(k)}} v _i m _i )+ z _k .

在这种情况下，用户 k的信干噪比(SINR)成为波束成形向量v _1:K (,v ₁ , · · ·, v _K )的函数，其表达式为
SINR _k (v _1:K ), |h ^† _k v _I(k) | ² / (∑ _{i∈[K]{I(k)}} |h ^† _k v _i | ² +1), (2)
用户k的可达速率变为R _k W log(1+ SINR _k (v _1:K ))，其中 W为总系统带宽。因此，用户 k所需的传输时间为 T _k , B/R _k 。

由于发射机通过空间复用为所有用户组提供服务，因此为服务所有用户所需的总传输时间变为
T, max _k∈[K] T _k = max _k∈[K] [ B/W log(1+ SINR _k (v _1:K ))] .

因此，我们求解如下问题：寻找最优用户组和最优波束成形向量以最小化总传输时间：
(P1) minimize _{(G 1 ,…,G K ) , (v 1 ,…, v K )} T
subject to
∑ ^K _k=1 ‖v _k ‖ ² ≤ P, (3)
G ₁ ∪… ∪ G _K =[K], (4)
G _i ∩ G _j = ∅ for all i ≠ j, (5)
M _k ⊃{Q _n | n∈G _I(k) {k}}for k∈[K],(6)

我们定义 P为针对所有可能内存状态的可解码团覆盖索引码集合
P,{(G ₁ ,…, G _K ) ∣ ∣ (4),(5)}. (7)

由于 T是SINR的单调递减函数，问题(P1)等价于
(P2) maximize _{(G 1 , ···, G K ) ∈ P, (v 1 ,…, v K )} min _k∈[K] SINR _k (v _1:K ) (8)
subject to(3),(6).

III. 两用户MISO广播信道中的激励性示例

在本节中，我们介绍一个简单的示例，展示多天线场景下索引编码与波束成形之间的依赖关系，从而引出 MISO广播信道中一种新的最优指数编码设计。为此，我们考虑一个双用户MISO广播信道，其中具有两个发射天线的发射机为两个各配备单天线的用户服务，即N _t = 2 和 K= 2。在此场景中，发射机有两种传输选择：
1) 如果发射机想要传输索引码 G ₁ ={1, 2} 和 G ₂ = ∅，则发射机需要使用多播波束成形来传输 Q ₁ ⊕Q ₂ 。
2) 如果发射机想要传输索引码 G ₁ ={1} 和 G ₂ {2}，则通过多用户波束成形以空间复用方式分别传输 Q ₁ 和 Q ₂ 。

请注意，在包括[5],索引码 G ₁ ={1, 2}和 G ₂ = ∅的传统设计中是最优的。接下来，我们为每种情况找到最优波束成形器。

A. 用于索引码 G ₁ ={1, 2} 和 G ₂ = ∅ 的多播波束成形器

当 G ₁ ={1, 2}和 G ₂ = ∅时，发射机使用多播波束成形发送Q ₁ ⊕Q ₂ ，以最大化两个用户的SINR的最小值。设多播波束成形器为v,[v ₁ , v ₂ ] ^T 。则问题(P2)的多播波束成形器可通过以下方式通过最大化最小SINR来确定： [12]。

引理1。 使服务两个用户所需的总传输时间最小的最优多播波束成形器可表示为
v= (‖h ₂ ‖ ² −|h ^† ₁ h ₂ |)h ₁ +(‖h ₁ ‖ ² −| h ^† ₁ h ₂ | )h ₂ e ^{jθ ₁₂} / √(‖h ₁ ‖ ² ‖h ₂ ‖ ² −| h ^† ₁ h ₂ | ² )(‖h ₁ ‖ ² +‖h ₂ ‖ ² −2|h ^† ₁ h ₂ |) √P.

在这种情况下，最优SINR由以下给出
SINR= ‖h ₁ ‖ ² ‖h ₂ ‖ ² −|h ^† ₁ h ₂ | ² / (‖h ₁ ‖ ² + ‖h ₂ ‖ ² − 2|h ^† ₁ h ₂ |) P, (9)
其中 θ ₁₂ 是复数h ^† ₁ h ₂ 的相位角。

B. 索引码 G ₁ ={1} 和 G ₂ ={2} 的零迫

当 G ₁ ={1}和 G ₂ ={2}时，空间复用的最优多用户波束成形可通过脏纸编码[13],实现，但为了保证解析易处理性，本例中我们采用零迫波束成形作为一种次优但实用的方法。对于双用户零迫波束成形，两个用户的波束成形向量分别为v ₁ = α ₁ [h ⁽²⁾ ₂ ,−h ⁽¹⁾ ₂ ] ^T 和v ₂ = α ₂ [−h ⁽²⁾ ₁ , h ⁽¹⁾ ₁ ] ^T ，其中 α ₁ 和 α ₂ 为缩放因子， h ^(j) _i 是信道向量h _i 的第 j个元素，即h ₁ =[h ⁽¹⁾ ₁ h ⁽²⁾ ₁ ] ^T 和h ₂ =[h ⁽¹⁾ ₂ h ⁽²⁾ ₂ ] ^T 。 α ₁ 和 α ₂ 的最优值被选择为最小化总传输时间 T，这等价于最大化两个用户SINR的最小值，结果为 |α ₁ | = |α ₂ | 和
|α ₁ | ² = |α ₂ | ² = P / (||h ⁽¹⁾ ₁ | ² +||h ⁽²⁾ ₁ | ² +||h ⁽¹⁾ ₂ | ² +||h ⁽²⁾ ₂ | ² ).

因此，相应的最优SINR变为
SINR= ||h ⁽¹⁾ ₁ h ⁽²⁾ ₂ − h ⁽²⁾ ₁ h ⁽¹⁾ ₂ | ² P / (|h ⁽¹⁾ ₁ | ² +||h ⁽²⁾ ₁ | ² +||h ⁽¹⁾ ₂ | ² +||h ⁽²⁾ ₂ | ² ). (10)

C. 比较

现在我们证明，在某些信道条件下，采用零迫波束成形的索引码{G ₁ ={1}, G ₂ ={2}}优于采用多播波束成形的索引码{G ₁ ={1, 2}, G ₂ = ∅}。通过比较公式(9)和(10)中的SINR，我们可以对以下信道条件下的最优索引码进行分类；令 φ ^(j) _i 表示i, j ∈{1, 2}对应的信道 h ^(j) _i 的角度。
注意，当信道条件满足φ ⁽¹⁾ ₁ +φ ⁽²⁾ ₂ −φ ⁽²⁾ ₁ −φ ⁽¹⁾ ₂ ≈ 0且 |h ⁽¹⁾ ₁ ||h ⁽²⁾ ₂ | −|h ⁽²⁾ ₁ ||h ⁽¹⁾ ₂ | ≈ 0时，公式(10)接近于零，因此采用多播波束成形的索引码{G ₁ ={1, 2}, G ₂ = ∅}优于采用零迫波束成形的索引码{G ₁ ={1}, G ₂ ={2}}。另一方面，当信道条件满足φ ⁽¹⁾ ₁ +φ ⁽²⁾ ₂ +φ ⁽²⁾ ₁ +φ ⁽¹⁾ ₂ = 0且 |h ⁽¹⁾ ₁ ||h ⁽²⁾ ₁ | −|h ⁽¹⁾ ₂ ||h ⁽²⁾ ₂ | ≈ 0时，公式(9)接近于零，因此采用零迫波束成形的索引码{G ₁ ={1}, G ₂ ={2}}更优。

因此，即使考虑单播传输中的次优波束成形器，该结果也清楚地表明最短码并不总是最优的，且在多天线情况下，最优索引码还依赖于信道条件，这促使了新的最优索引码搜索算法的研究。

IV. 索引码与波束成形器的联合设计

由于问题(P2)无法直接求解，我们通过两个步骤来解决该问题(P2)。首先，针对任意给定的索引码 {G ₁ ,…, G _K }设计波束成形向量，然后利用所提波束成形器寻找最优索引码。
对于任意给定的索引码 {G ₁ , · · ·, G _K }，我们可以将问题 (P2)表述如下：
(P3) maximize _{{v 1 ,…,v K }} min _k∈[K] SINR _k (v _1:K ) (11) subject to(3).

由于波束成形向量v _i 用于组 G _i 中的用户，问题(P3)可视为一个通用多播波束成形问题，该问题是NP难的[14]。因此，我们提出了一种基于共轭梯度的多组多播波束成形器 （CGB）[15]。

A. 基于共轭梯度的多组多播波束成形器

(11) 中的最小SINR值是相同的
min _k∈[K] [|h ^† _k v _I(k) | ² / (∑ _{i∈[K]{I(k)}} |h ^† _k v _i | ² +1)].

因此，为了应用梯度下降算法，我们将问题(P3)转化为一个带有辅助参数 η[16]的等效参数化规划问题，如下所示：
(P4) maximize _{{v 1 ,…,v K }} (min _k∈[K] f _k (v _1:K , η)) subject to(3),

其中
f _k (v _1:K , η), |h ^† _k v _I(k) | ² − η ·( ∑ _{i∈[K]{I(k)}} |h ^† _k v _i | ² +1).

我们定义 F(v _1:K ,η), min _k f _k (v _1:K ,η)，这是一个非光滑函数。
因此，使用对数‐指数平滑函数，我们将目标函数进行变换为
F(v _1:K , η, µ), µ log(∑ _k∈[K] exp(−f _k (v _1:K , η)/µ))
并重写问题(P4)为
(P5) maximize _{{v 1 ,…,v K }} F(v _1:K , η, µ) subject to(3).

我们可以使用Dinkelbach型黎曼共轭梯度（DT‐RCG）算法[15], 来求解问题(P5)，该算法是一种用于流形优化的梯度下降算法。
然而，共轭梯度法仅能保证收敛到局部极值点，如果算法的起始点选择不当，则可能导致所得解远离最优解。因此，设置一个良好的初始波束成形器，使解收敛到全局极值点显得尤为重要。

B. 初始化：基于两阶段ZF的多播波束成形器

作为CGB的初始波束成形向量，我们采用基于两阶段ZF的多播波束成形（TZFMB），因为该方法简单且性能相对较好。为了符号表示的简便，我们首先将 G̃ _i 定义为不属于 G _i 的用户集合（即 G̃ _i ,[K]\G _i ）。然后，我们为第i个用户组 G _i 定义一个矩阵 ˜H _i ，该矩阵由不在 G _i 中的其他用户的信道系数向量拼接而成，即 ˜H _i , [h _{k 1} · · · h _{k u} ] ∈ C ^{N _t ×| G̃ _i |} ，其中 k ₁ · · · k _u ∈ G̃ _i ，且 | · | 为集合的基数。
然后，对于每个组，我们设计一个零强制波束成形器(ZFB)，以消除用户组之间的组间干扰，即v _i ∈Null (˜H _i )。
我们定义w _i1 , · · ·, w _in 为每个用户组 G _i 的零空间的基向量。因此，用户组 G _i 的零强制波束成形器(ZFB)通过基向量的线性组合得到：
v _i = p _i1 w _i1 + · · ·+ p _in w _in = W _i p _i , (12)
其中p _i ,[p _i1 , · · ·,p _in ] ^T 是第 i个用户组的线性组合系数，且 W _i ,[w _i1 · · · w _in ]。利用(12)，式(2)中用户 k的SINR变为h ^† _k W _I(k) p _I(k) = | h ^† _k,eff p _I(k) | ² ，其中h _k,eff 定义为h _k W _I(k) 。因此，问题(P3)可转化为
(P6) maximize _{p 1 ,···, p K} min _k∈[K] |h ^† _k,eff p _I(k) | ² subject to ∑ _i∈[K] ‖p _i ‖ ² ≤ P
由[17],问题(P6)的解可计算为p _i = γ _i ˆp _i /‖ˆp _i ‖，其中 γ _i 是功率分配，使得每个组内的最小SINR在不同组之间相等，而ˆp _i 是通过求解以下最大最小公平多播波束成形器得到的：
(SP1) maximize _ˆp min _{k∈G i} |h ^† _k,eff p̂ _i | ² subject to ‖p̂ _i | ² ≤ 1
通过半定松弛（SDR）获得的(SP1)的近最优解[14]。在求得ˆp _i 后，对于每个 i， γ _i 可直接计算得出
γ ² _i = min _{k∈G i} |h ^† _k,eff p _I(k) | ² / ∑ _j∈[K] min _{k∈G j} |h ^† _k,eff p _I(k) | ² P. (13)

C. 最优索引码搜索

由于已经为任意索引码构建了波束成形，问题(P2)简化为以下问题：
(P7) maximize _{{G 1 ,…,G K }∈P} min _k∈[K] SINR _k (v? _1:K ) subject to(6).

然后，我们可以通过求解问题(P7)来找到最佳索引码及相应的波束成形器。由于可解码索引码集合无法以结构化方式给出，因此我们首先需要在用户给定的存储信息（即存储状态）下，在所有可能的索引码中找出所有可解码索引码。接着，通过比较这些可解码索引码在问题(P7)中的目标函数值，即可在可解码索引码中找到最优的一个。
由于每个索引码的波束成形向量应表示为多播波束成形器，而该多播波束成形器没有闭式解，因此无法将任意波束成形向量显式地表示为索引码的函数。因此，我们无法避免采用穷举搜索算法来寻找最优解。然而，幸运的是，对于团覆盖索引编码，可解码索引码的数量是有限的，因此可以通过在给定存储状态下对可解码索引码进行有限搜索，找到问题(P7)的解。

我们可以使用大O符号粗略地表示所提方案在最坏情况下的复杂度。由于我们考虑团覆盖索引码，当每个用户的内存大小为 M时，总的可解码团索引码数量最多为 2 ^M 。然后，我们需要为每个索引码寻找波束成形器以选择最佳的一个。
对于TZFMB，我们最多需要找到 K个波束成形器，其中每个波束方向通过求解问题(SP1)并结合功率分配（例如(13)中的 γ _i ）获得，其对应的复杂度分别为O(K ³ N ⁶ _t + K ² N ² _t ) [14]和 O(KN _t )。因此，TZFMB的复杂度变为 O(K ⁴ N ⁶ _t + K ³ N ² _t +K ² N _t )。此外，对于CGB，我们首先找到两阶段零强迫多播波束成形器作为初始点，为了进一步优化，每次迭代都需要计算共轭梯度，其复杂度为 O(K ³ N _t ) [15]。因此，允许最多 r次迭代时，总复杂度变为 O(K ⁴ N ⁶ _t + K ³ N ² _t + K ² N _t + rK ³ N _t ) 。综上所述，使用TZFMB和CGB的索引编码的总复杂度分别为 O(2 ^M [K ⁴ N ⁶ _t + K ³ N ² _t + K ² N _t ]) 和O(2 ^M [K ⁴ N ⁶ _t + K ³ N ² _t + K ² N _t + rK ³ N _t ]) 。

V. 仿真结果

在本节中，我们从总传输时间的角度评估了所提出的索引编码和波束成形设计。为了进行比较，我们考虑了以下六种不同的方案。
•(传统方案1) 使用时分复用（TDM）的单播
•(传统方案2) 使用ZFB的单播
•（传统方案3）使用CGB的单播 [15]
•（传统方案4）基于TDM的指数编码 [7]
•（所提出的方案1）使用TZFMB的指数编码（第四节‐B）
•（所提出的方案2）使用CGB的指数编码，其中 TZFMB用于初始波束成形器（第四节‐A）
注意，[9]–[11] 的波束成形方案仅针对均匀内存状态设计，因此不适用于指数编码问题中考虑的任意内存状态。

我们考虑一个具有五根发射天线的发射机为五个用户服务的场景，其中发射机拥有由20个 10 ⁵ 比特文件组成的文件库，每个用户在缓存中存储十个文件，即(N _t , K, N, B, M)=(5, 5, 20, 10 ⁵ , 10)。同时，总带宽为20兆赫 （即 W=2 × 10 ⁷ ）。用户内存状态任意给定，而每个文件以相同概率存放在每个用户的内存中（即等概率缓存）。

图2比较了各种方案在不同发射信噪比（SNR）下为所有用户服务所需的总传输时间。我们可以观察到，无论是单播还是索引编码，空间复用方案在所有SNR区域均优于时分复用方案，这表明在这两种情况下，我们都可以获得由多个发射天线提供的空间复用增益以及索引编码增益。在低SNR区域，共轭梯度法相比基于两阶段ZF的多播波束成形器表现出更好的性能。然而，由于系统在高SNR区域变得干扰受限，因此无需对SINR平衡（即梯度波束成形）进行复杂的考虑，此时基于两阶段ZF的多播波束成形器已足够。因此，在图中高SNR区域，共轭梯度多组多播波束成形器与两阶段波束成形器具有相同的性能。尽管由于篇幅限制无法添加更多图表，但我们的所提出的方案在更一般的设置下（如任意文件库大小和任意用户内存大小）相比传统方案显著减少了总传输时间。

VI. 结论

本文探讨了多天线下的指数编码传输。我们在双用户 MISO广播信道中的简单示例揭示了索引码与多播波束成形之间联合设计的潜力。然而，由于最优联合设计问题本身就是NP难的，我们采用了两步设计方法，即首先为任意索引码找到梯度多组多播波束成形器，然后找出索引码与其对应波束成形器的最佳组合，并分析了复用指数码的增益。仿真结果表明，联合索引编码和波束成形设计能有效减少所有信噪比区域的总传输时间。