排序算法：冒泡排序

冒泡排序的思想与其他排序相比比较简单；其大致思想就是遍历顺序表或数组，每一次遍历都将最大的数据放到后边。

用一个数组来举例子

 

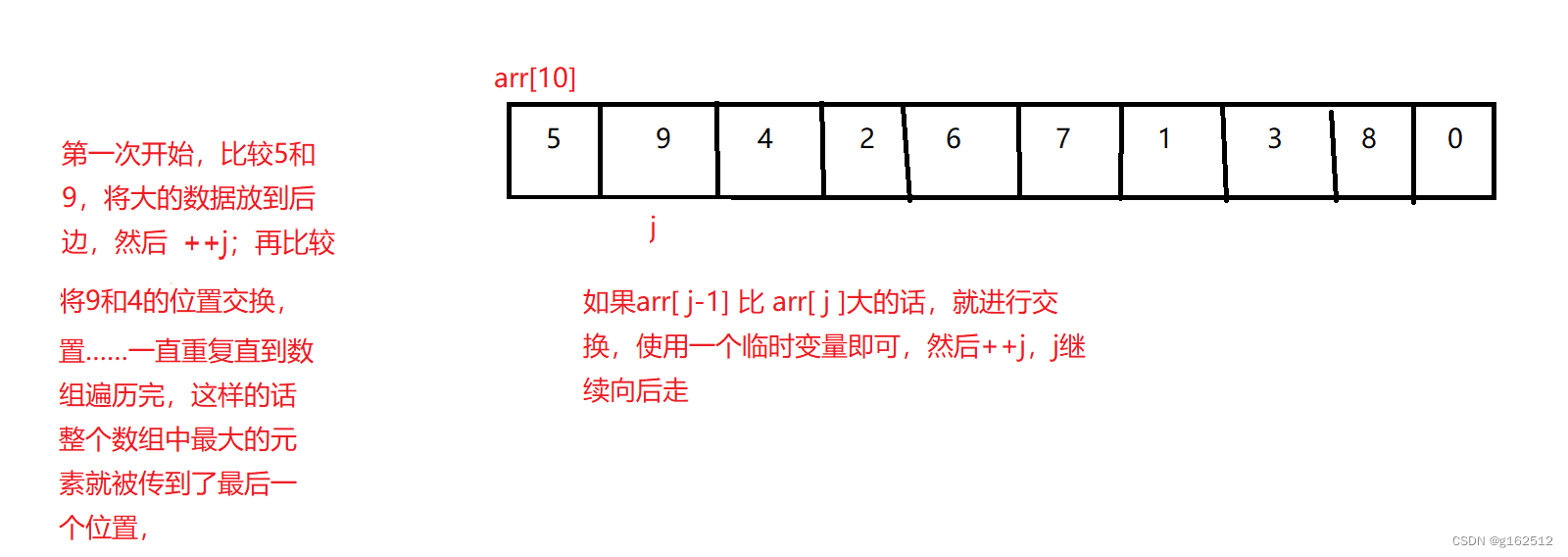
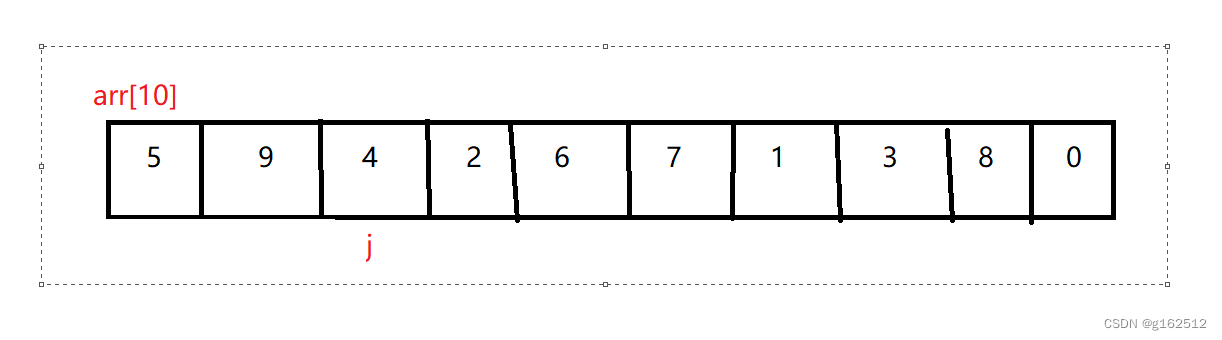
 当arr[ j-1 ] >arr[ j ]的时候，使用一个临时变量tmp交换俩个元素；交换完 j 再+1；

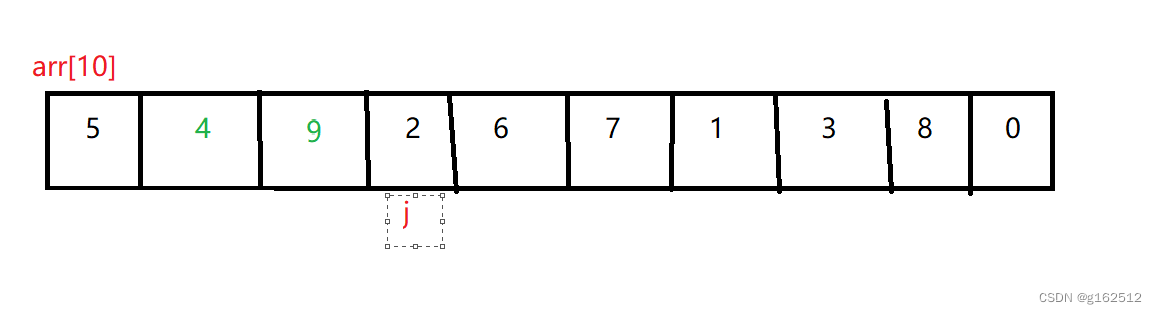再次进行比较是否arr[ j-1 ] >arr[ j ]，如果是的话就交换俩个元素。

一直走到结束，9就被放到了最后

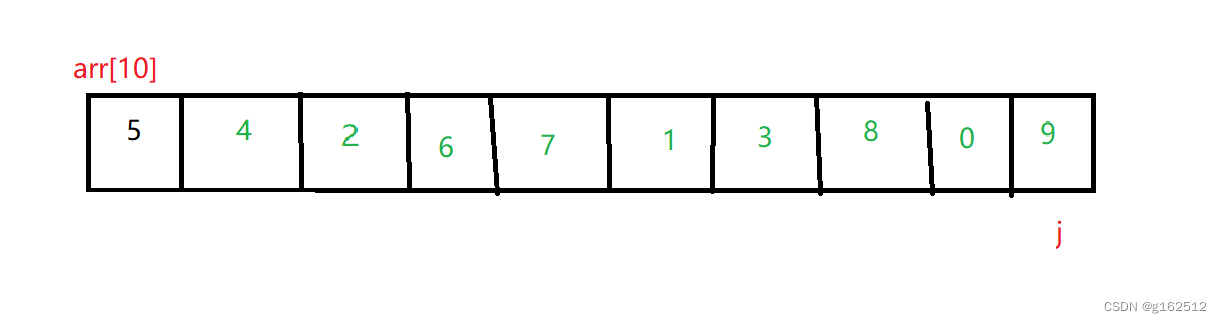
但是，这仅仅只是一次冒泡，只是把最大的元素9放到了最后，还要进行第二次冒泡，并且这次冒泡不需要最后一个元素的参与，因为上一次冒泡已经确定了它是整个数组中最大的元素了。

再让j 回到起始的1号位置，再进行一趟冒泡，这次交换完，显然8被放到了最后，并且前面元素也越来越有序；

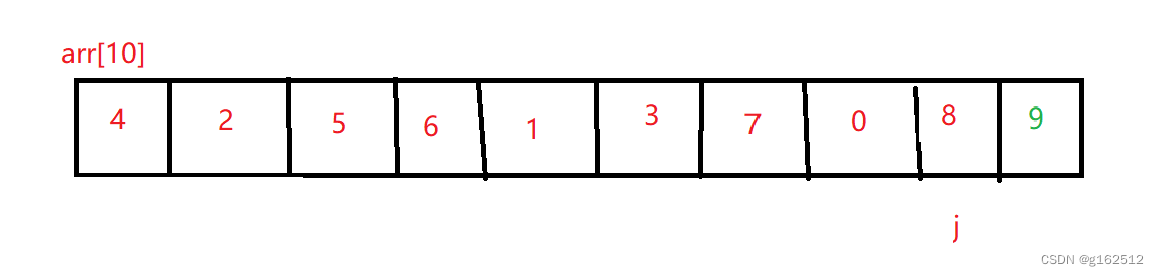接下来在进行下一次冒泡的时候，就不需要去考虑后俩个元素了，因为这俩个元素已经是有序的并且是最大的元素。

 当我们排序完9次以后，数组一定是有序的了，因为最小的元素0已经被交换到前面来了，一个元素一定是有序的，而后面9个元素也是有序的，所以n的数据进行冒泡排序需要执行n-1次。

 冒泡排序的算法时间复杂度为O(n^2)，空间复杂度为O(1)；并且是一个稳定的算法，因为它需要每个元素遍历一次。

并且冒泡算法还是有一些优化的空间：

比如说数组为{ 1,2,3,5,4 };

当我们进行一趟冒泡后，从第二趟开始就已经没有意义了，数组已经是完全有序的了，这样我们就可以设置一个标记位置，如果说冒泡过程中没有发生元素的交换，那么我们认为数组是完全有序的，就可以直接跳出循环，排序也就结束了。

下面是冒泡排序的代码 

const int SIZE = 10;
int main()
{
    int tage=true;
	int arr[SIZE] = { 5,1,68,43,2,8,75,21,10,0 };
	for (int i = 0; i < SIZE; ++i)
	{
        tage=true;
		for (int j = 1; j < SIZE - i; ++j)
		{
			if (arr[j-1] > arr[j])
			{
				int tmp = arr[j];
				arr[j] = arr[j - 1];
				arr[j - 1] = tmp;
                tage=false;
			}
		}
        if(tage)
        {
            break;
        }
	}
	for (int i = 0; i < SIZE; ++i)
	{
		cout << arr[i] << "  ";
	}
	return 0;
}

感谢阅读！