1.1.1 坐标系

更多内容，请关注：
github：https://github.com/gotonote/Autopilot-Notes.git）

在自动驾驶和机器人的多传感器融合定位算法中，想要获得鲁棒的、连续的、精确的全局定位结果，通常会充分利用各个传感器和模型，比如 GNSS/IMU/轮速编码器/载体模型/camera/LiDAR/高精地图，这其中会涉及到两大类坐标系，一个是常见的全局坐标系，也可以叫做地理坐标系或导航坐标系，算法最终的定位结果、GNSS/高精地图的输入都与此相关，另一个是局部坐标系，用于表示载体自身或者其上各个传感器的位置和朝向，IMU/轮速编码器/载体模型/camera/LiDAR的输入数据都在各自的局部坐标下。

一、ECEF 坐标系

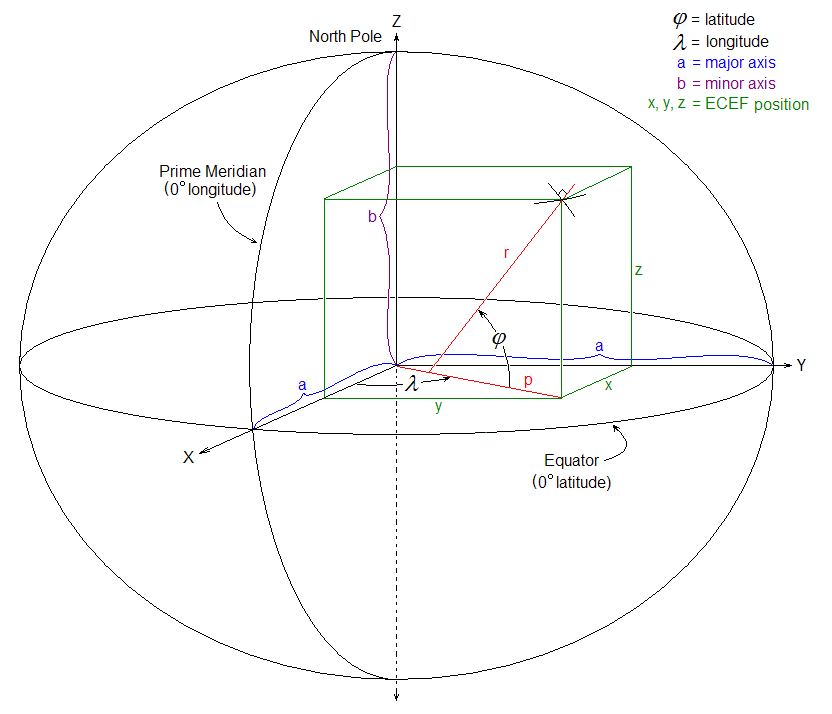
ECEF（Earth-Centered Earth-Fixed ）地心地固坐标系，ECEF坐标系与地球固联，且随着地球转动。图中O即为坐标原点，位置在地球质心。X轴指向本初子午线（0度经度）和赤道（0deglatitude）的交点。Z轴通过原点指向北极。Y轴与X、Z轴构成右手坐标系。地球附近空间的点都可以在此坐标系下表示为 (x, y, z)。图中 (a, b) 分别为大地椭球的长轴和短轴，对于大地椭球不同的几何形状定义会导致不同的 ECEF 系，WGS84 就是最常见的一种 ECEF 系。

在 ECEF 坐标系下的点 $(x,y,z)$ 也可以用经纬高 $(\lambda ,\varphi ,h)$ 来表示：

$$\begin{array}{rl}x& =(N+h)cos\varphi \cdot cos\lambda \\ y& =(N+h)cos\varphi \cdot sin\lambda \\ z& =[N(1-e^2)+h]sin\varphi \end{array}$$

• e：椭球偏心率， $e^2=\frac{a^2-b^2}{a^2}$ ， a：长半径，b：短半径；
• N ：基准椭球体卯酉圈曲率半径， $N=\frac{a}{\sqrt{1-e^{2}si{n}^2\varphi }}$ ；

反过来已知 ECEF 值，也能求解经纬高，但由于 h 的计算式含有待求解的 φ ，所以我们只能借助迭代法来逼近求解 φ 和 h 的值，通常收敛得很快，经过 3~4 次迭代就可以结束计算。

λ = a r c t a n ( y x ) h = p c o s ϕ