本文通过四个经典的动态规划问题——装配线调度、矩阵链乘、最长公共子序列和最大子数组，详细阐述了动态规划的四步解题方法。每个问题都包括最优子结构的识别、递归关系的定义、自底向上的解决方案构建以及最优解的构造。通过实例解析和代码实现，展示了如何运用动态规划解决实际问题。
DP的一般求解步骤：
1.表征最优解的结构(确定是否具有最优子结构)
2.递归定义最优解的值（找出问题最优解与子问题最优解的递归关系，并给出递归式)
3.以自下而上的方式计算解的值(利用递归关系转化为非递归的算法)
4.使用计算的信息构建最优解
(1)Assembly lines（装配线调度问题）
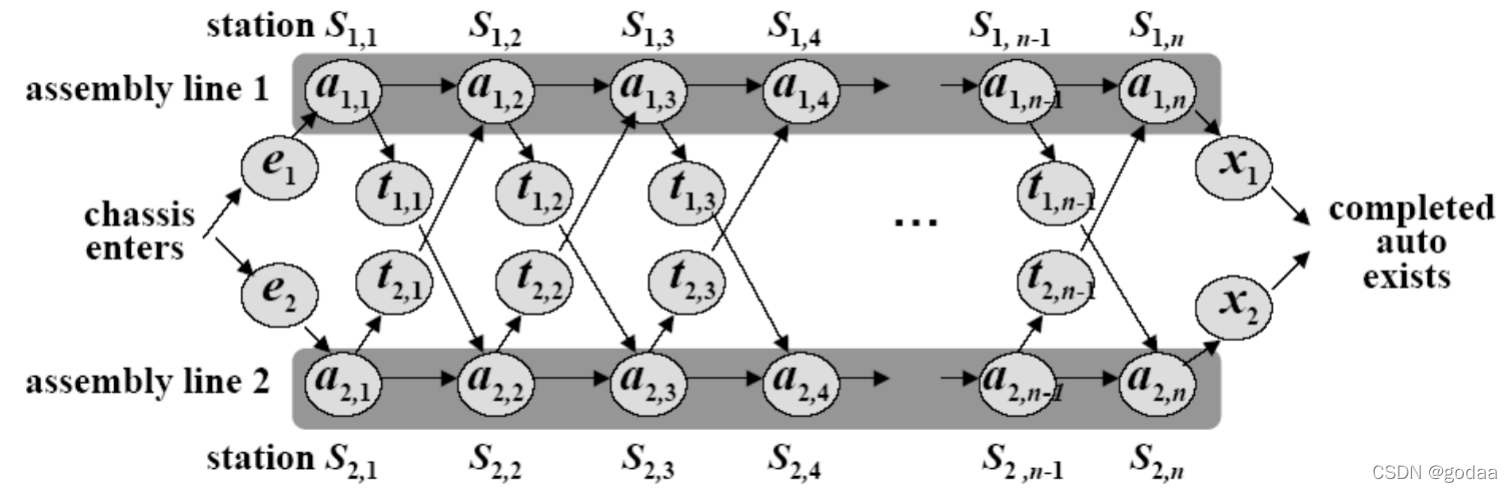
Problem description：
- n stations on each line: S1,1…S1,n and S2,1…S2,n .（有两个并排的调度线路）
- ai, j : time required on line i at station j.（aij表示通过站台Sij所需时间）
- Transferring times: ti, j .（若想从S1,j过渡到S2,j+1或S2,j过渡到S1,j+1，耗费时间是ti,j)
- Entry and exit time: e1 , e2 , x1 , x2.(起始进入和退出时间）
- Goal: Find the fastest path through the factory.（找一个时间最短的路径）
- tips：Trying all possibilities is not tractable.（建议不要暴力求解）
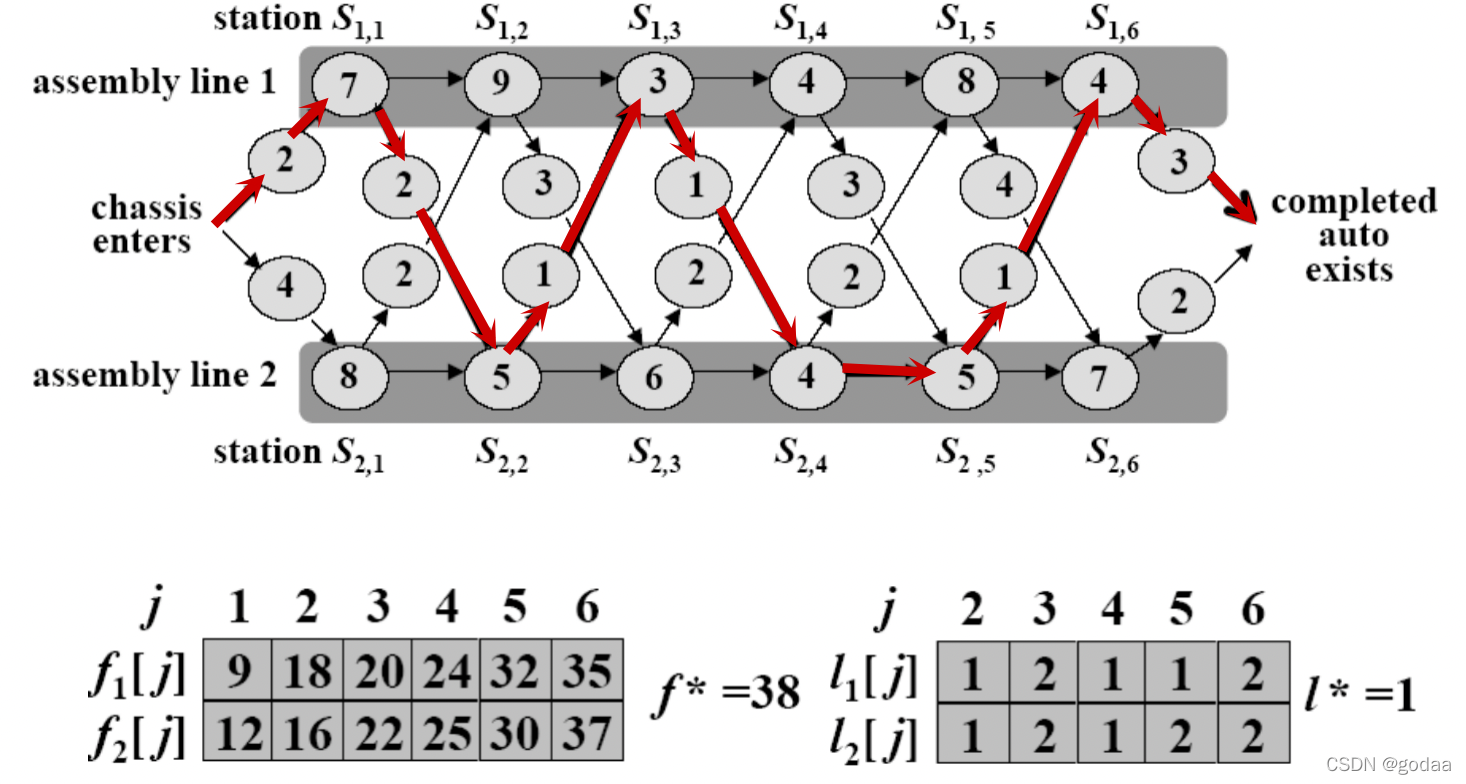
用DP四步骤求解
(i) 要求整个过程花费时间最短，那么通过站台Si,j都应该花费时间是最少的，例如要求通过站S1,j的最短时间，就必须必须先求通过站S1,j-1和S2,j-1的最短时间，要求通过站S2,j的最短时间，也必须先求通过站S1,j-1和S2,j-1的最短时间.这就是问题的最优子结构。
(ii) 定义通过站Si,j的最短时间为f(i,j)，则通过整条装配线的最短时间ff= min{f(1,n)+x1,f(2,n)+x2}，而对于f(i,n)的求解有如下递归式:
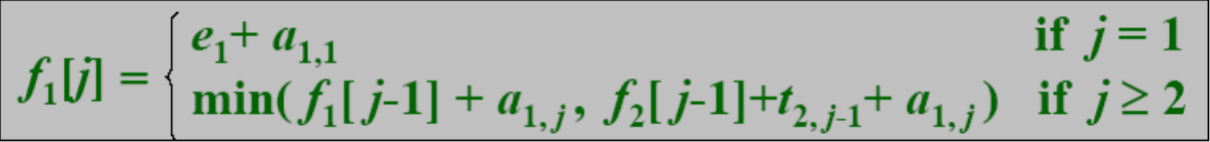
(iii) 先求出f(1,1)和f(2,1)，然后根据递归式依次推出f(1,2),…,f(1,n)以及f(2,2),…,f(2,n)的值，最后综合这两个求一个最小值ff也就求出来了。
(iv) 对于本问题，若只求通过装配线的最短时间，则上面几个步骤即可求出。若还要求给出具体最短时间的装配路线，则还要构造出最优解结构。为完成此任务，应在步骤 (iii) 过程中记录被通过站Sij的最快装配路线所使用的前一站j-1，最后根据递推得出最优解。
代码实现：
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int e1,e2,x1,x2,ff=0;
//起始下标都从1开始
int[][] a = new int[3][n+1];
int[][] t = new int[3][n];
int[][] f = new int[3][n+1];
int[][] l = new int[3][n+1];
//输入起始时间
e1 = sc.nextInt();
e2 = sc.nextInt();
//输入aij
for (int i = 1; i <= 2; i++) {
for (int j = 1; j <= n; j++) {
a[i][j] = sc.nextInt();
}
}
//输入tij
for (int i = 1; i <= 2; i++) {
for (int j = 1; j <= n-1; j++) {
t[i][j] = sc.nextInt();
}
}
//输入结束时间
x1 = sc.nextInt();
x2 = sc.nextInt();
//初始化
f[1][1] = e1 + a[1][1];
f[2][1] = e2 + a[2][1];
for (int j = 2; j <= n; j++) {
//求整个一号线的最短时间
if(f[1][j-1]+a[1][j] <= f[2][j-1]+t[2][j-1]+a[1][j]){
f[1][j] = f[1][j-1]+a[1][j];
l[1][j] = 1; //代表上一站是从1号线过来
}else{
f[1][j] = f[2][j-1]+t[2][j-1]+a[1][j];
l[1][j] = 2;//代表上一站是从2号线过来
}
//求整个二号线的最短时间
if(f[2][j-1]+a[2][j] <= f[1][j-1]+t[1][j-1]+a[2][j]){
f[2][j] = f[2][j-1]+a[2][j];
l[2][j] = 2;
}else{
f[2][j] = f[1][j-1]+t[1][j-1]+a[2][j];
l[2][j] = 1;
}
}
int k ;
if(f[1][n]+x1 <= f[2][n]+x2){
ff = f[1][n]+x1;
k = 1; //最后结束时的上一站为1，也即第n站是从1号线过来的
}else{
ff = f[2][n]+x2;
k = 2;//最后结束时的上一站为2，也即第n站是从2号线过来的
}
System.out.println("最快时间为： "+ff);
//打印最优解
System.out.println(k+" lines"+" station "+n);
for (int j = n; j>=2 ; j--) {
k = l[k][j]; //得到上一站，例如l[1][n]=2就代表n-1站是从2号线过来的，依次逆推可以得到完整路线
System.out.print(k+" lines"+" station "+(j-1));
System.out.println();
}
示例：
(2)Matrix-chain multiplication problem(矩阵链乘问题）
Problem description：
- Goal. Given a sequence of matrices A1,A2,…,An, find an optimal order of multiplication.(给定你一个矩阵序列，找出一个最优链乘的顺序）
- Multiplying two matrices of dimension p×q and q×r, takes time which is dominated by the number of scalar multiplication, which is pqr.（将两个维度为 p×q 和 q×r 的矩阵相乘，所花费的时间主要取决于标量乘法的次数，即 p * q * r）
- Generally. Ai has dimension pi-1×pi and we’d like to minimize the total number of scalar multiplications.(一般来说, 矩阵Ai 的维数为 pi-1×pi，我们希望最小化标量乘法的总数)
问题示例：
DP四步骤求解：
(i) 设Ai,j表示Ai,Ai+1,…,Aj通过加括号得到的一个最优计算模式，且恰好在Ak与Ak+1之间分开。则“前缀”子链Ai,Ai+1,…,Ak必是一个最优的括号化子方案，记为Ai,k；同理“后缀”子链Ak+1,Ak+2,…,Aj也必是一个最优的括号化方案，记为Ak+1,j。(这就是最优子结构)
(ii) 对于矩阵链乘问题，将所有对于1 <= i <= j <=n确定为Ai,Ai+1,…,Aj的最小代价括号化方案作为子问题。令m[i,j]表示计算矩阵Ai,j所需要的标量乘法的次数最小值，则最优解是计算Ai,n所需的最小代价就是m[1,n].
递归定义m[1,n]：
a. 对于i=j的情况，显然有m=0，不需要做任何标量乘法运算，所以对于所有i=1,2,…,n有m[i,i]=0。
b. 对于i<j的情况，就按照最优括号化方案的结构进行计算m[i,j]，假设最优括号化方案的分割点在Ak和Ak+1之间，那么m[i,j]的值就是Ai,k和Ak+1,j的代价加上两者标量乘法的代价的最小值，即:m[i,j]=m[i,k]+m[k+1,j]+Pi-1 * Pk * Pj。该公式的假设是最优分割点是已知的，但实际上不知道。然而，分割点k只有j-i种情况取值。由于最优分割点k必定在i~j中取值，所以只需要遍历检查所有可能的情况，找到最优解即可，可以得出一个递归公式：
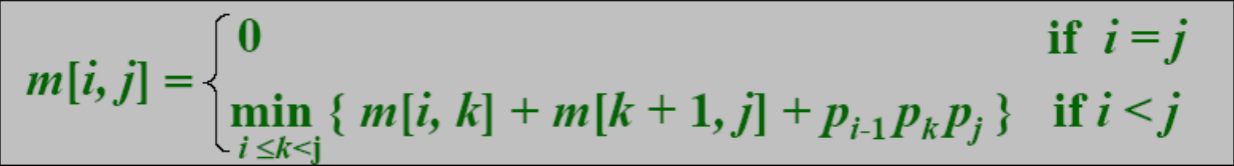
(iii,iv) m[i,j]只是给出了子问题最优解的代价，但是并未给出构造最优解的足够信息(即分割点的位置信息)所以，在此基础上，使用一个二维数组si,j来保存Ai,Ai+1,…,Aj的分割点位置k，采用自底向上表格法来代替上述递归公式算法计算最优代价。过程中假定矩阵A的规模为Pi-1 * Pi，输入P=<p0,p1,…,pn>，长度为p.length=n+1，其中使用一个辅助表m来记录代价m[i,j]，另一个表s来记录分割点的位置信息，以便构造出最优解。（构造最优解）
代码实现:
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt(); //4，输入矩阵个数
int[] p = new int[n+1]; //矩阵基数
int[][] m = new int[n+1][n+1]; //代价数组
int[][] s = new int[n+1][n+1]; //分割点数组
for (int i = 0; i <= n; i++) {//10 20 50 1 100
p[i] = sc.nextInt();
}
for (int i = 1; i <=n; i++) {
m[i][i] = 0;
}
for (int l = 2; l <= n; l++) {
for (int i = 1; i <= n-l+1; i++) {//前面两个for类似排列组合，先是两两矩阵的不同组合，再是3个矩阵的不同组合...
int j = i+l-1;//A1A2 A2A3 A3A4--> A1A2A3 A2A3A4---> A1A2A3A4
m[i][j] = Integer.MAX_VALUE;//(1,2)(2,3)(3,4)|(1,3)(2,4)...
for (int k = i; k < j; k++) { //寻找Ai~Aj的最优分割点
int q = m[i][k] + m[k+1][j] + p[i-1]*p[k]*p[j];
if(q < m[i][j]){
m[i][j] = q;
s[i][j] = k;//保存最优分割点
}
}
}
}
//输出m[1,n]，m[1,n]就是整个矩阵链乘的最小代价
System.out.println(m[1][n]);
//打印最优解
printS(s,1,n);
}
//((A1 (A2 A3)) A4
private static void printS(int[][] s,int i,int j) {
if (i == j)
System.out.print("A" + i);
else {
System.out.print("(");
printS(s, i, s[i][j]);//递归打印i到k前缀矩阵，s[i][j]就是k即分割点
printS(s, s[i][j] + 1, j);//递归打印k+1到j后缀矩阵
System.out.print(")");
}
}
/**
测试用例：
6
30 35 15 5 10 20 25
15125
((A1(A2A3))((A4A5)A6))
**/
(3)Longest Common Subsequence(最长公共子序列)
Problem description：
Given two sequences x[1…m] and y[1…n], find a longest subsequence common to then both.
DP四步骤求解：
(i) 要求X={x1,12,…,xm}和Y={y1,y2,…,yn}的的最长公共子序列，必须求出Xm-1和Yn-1的最长子序列再加1或者求出Xm和Yn-1以及Xm-1和Yn的最长公共子序列中的较大者，这就是最优子结构。
(ii) 求Xm和Yn的最长公共子序列可分为两种情况：
a. 当xm = yn时，求出Xm-1和Yn-1的最长公共子序列加上1就是原问题的最优解。
b. 当xm != yn时，求出max{L[i][j-1]，L[i-1][j]}即为原问题的最优解，其中用L[i][j]表示Xi与Yj的最长公共子序列长度，递归式如下：
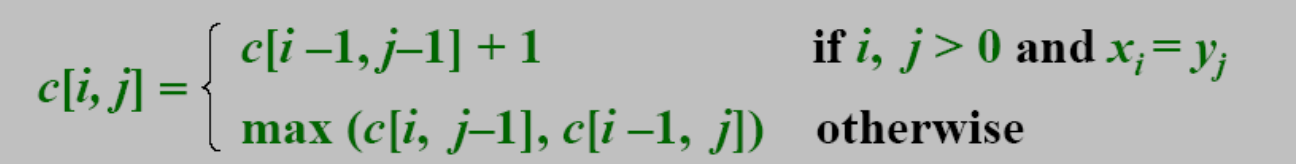
(iii,iv) 为了得到序列Xm和Yn具体最长公共子序列，设二维数组S[m+1][n+1]，其中S[i][j]表示在求L[i][j]的过程中的搜索状态。
若S[i][j]=1，表明xj = yj，则下一个搜索方向是S[i-1][j-1];若S[i][j]=2,表明下一个搜索方向是S[i][j-1]；若S[i][j]=3，表明下一个搜索方向是S[i-1][j]；
代码实现：
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int m = sc.nextInt();
int n = sc.nextInt();
char[] X = new char[m+1]; //Xm
char[] Y = new char[n+1]; //Yn
int[][] l = new int[m+1][n+1]; //长度表
int[][] s = new int[m+1][n+1]; //搜索路径表
char[] z = new char[n>m?n:m]; //存储最长公共子序列
for (int i = 1; i <= m; i++) {
X[i] = sc.next().charAt(0);//输入Xm
}
for (int i = 1; i <= n; i++) {
Y[i] = sc.next().charAt(0); //输入Yn
}
for(int i=0;i<=m;i++){// //初始化第0行
l[i][0]=0;
}
for(int j=0;j<=n;j++){// //初始化第0列
l[0][j]=0;
}
for (int i = 1; i <= m; i++) {//将递归式子转化为自下而上算法求解
for (int j = 1; j <= n; j++) {
if(X[i] == Y[j]){
l[i][j] = l[i-1][j-1]+1;
s[i][j] = 1;
}else{
l[i][j] = Math.max(l[i][j-1],l[i-1][j]);
if(l[i][j-1] >= l[i-1][j]){
s[i][j] = 2;
}else{
s[i][j] = 3;
}
}
}
}
int i = m,j= n;
int cnt = 0;
//l[m][n]即为Xm和Yn的最长公共子序列的长度
System.out.println("最长公共子序列长度为："+l[m][n]);
System.out.print("最长公共子序列是：");
while(i>0 && j>0){
if(s[i][j] == 1){ //朝着s[i-1][j-1]方向搜索
z[cnt++] = X[i];
i--;j--;
}else if(s[i][j] == 2){//朝着s[i][j-1]方向搜索
j--;
}else{//朝着s[i-1][j]方向搜索
i--;
}
}
//逆序输出
for (int p = cnt-1; p >=0; p--) {
System.out.print(z[p]+" ");
}
}
(4)Maximum Subarray（最大子数组）
Problem description: you are given n integers (there may be negative ones but not all) a1,a2,…,an, determine i and j which maximize the sum from ai to aj .
Case: 6 integers: (-2，11，-4，13，-5，-2)
Ans: i = 2, j = 4, max sum is 20.
DP四步骤求解：
(i) 假设m[i]表示以元素num[i]为结尾的连续子数组最大和，则必须求出m[i-1]以及nums[i]，这就是最优子结构。
(ii) 要求m[I]分两种情况
a. 若m[i-1]<=0,那么m[i-1]+nums[i]<=nums[i],也即m[i]=nums[i]
b. 若m[i-1]>0,那么m[i-1]+nums[i]>nums[i],也即m[i]=nums[I]+m[i-1]
综上 m[i] = max{m[i-1]+nums[i] , nums[I]}。最后用一个sum值保存m[i] (1<=i<=n)的最大值，这个最大值就是最优解。
m[i]的递归式如下： m[i] = max{m[i-1]+nums[i] , nums[i]}(1<=i<=n),最后根据递归式以非递归的方式自下而上求解出最优解。
(iii,iv) 每当sum值更新的时候，记录m[i]的i值。每当m[j] = nums[j]时记录j值。则迭代结束最优解即为下标为i~j的子数组，sum是最大子数组和。
代码实现：
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[] nums = new int[n+1];
int[] m = new int[n+1]; //m[i]记录以nums[i]元素结尾的最大子数组和
int sum = Integer.MIN_VALUE;
for (int i = 1; i <= n; i++) {
nums[i] = sc.nextInt();
}
m[1] = nums[1]; //初始化
int start = 1,end = 1; //最大子数组下标的起始和结束，初始只有一个元素，所以起始和结束都等于这个元素的下标
for (int i = 2; i <= n ; i++) { //自下而上求最优解
if(m[i-1]>=0){
m[i] = nums[i] + m[i-1];
}else{
m[i] = nums[i];
start = i; //舍去了m[i-1],首元素下标发送变化
}
if(sum < m[i]){
sum = m[i];
end = i; //更新最大值，记录此时结尾元素的下标
}
}
System.out.println("最大子数组和为："+sum);
System.out.print("最大子数组为：");
for(int i = start; i<= end; i++){
System.out.print(nums[i]+" ");
}
}
DP总结
DP有如下两个特征：
a. 最优子结构： 问题的最优解包含了子问题的最优解，贪心算法和分治法同样具有此特征。
b.重叠子问题： 解原问题的递归算法可反复地解同样的子问题，而不是总在产生新的子问题。分治法不同，它在递归的每一步都产生全新的子问题。
注： 当一个问题的最优解包含其子问题的最优解时，称此问题具有最优子结构。问题的最优子结构性质是该问题可用动态规划算法或贪心算法求解的关键特征。
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
