二叉树的最大深度

给定一个二叉树 root ，返回其最大深度。

二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

示例 1：

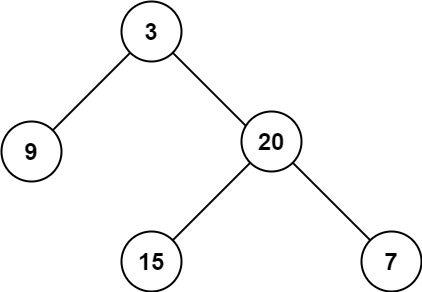
输入：root = [3,9,20,null,null,15,7]
输出：3

示例 2：

输入：root = [1,null,2]
输出：2

提示：

• 树中节点的数量在 [0, 104] 区间内。
• -100 <= Node.val <= 100

二叉树

定义：二叉树是有n(n>=0)个节点的有限集合，满足以下条件：

     （1）该集合或者为空(n=0);

     （2）或者由一个根节点以及两个不相交的子树（左子树和右子树）组成的非空树；

     （3）左右子树都为二叉树

值得注意的是，二叉树是一个递归的形式（即解决二叉树的相关题目要使用递归的思想）因为在一个二叉树中，每个节点最多有两个子节点，分别为左右节点，对于任意一个节点，在它的左子结点和右子节点上又分别可以构成两个独立的子树，这样就形成了一个递归的形式

满二叉树

一个二叉树若每一层的节点数都达到了最大值，则这个二叉树就是满二叉树；

完全二叉树

对于深度为k，有k个节点的二叉树，当且仅当其每一个节点都与深度为k的满二叉树中编号为1

到n的节点一一对应时，则称其为完全二叉树；

完全二叉树是由满二叉树引出来的，满二叉树是特殊的完全二叉树

二叉树的基本操作

1、遍历

先序遍历：先输出根节点——>左子结点——>右子节点

public void perOrder(TreeNode root)
{
    if(root==null)
         return;
    else{
        System.out.println(root.val+" ");
        perOrder(root.left);
        perOrder(root.right);
}

中序遍历：先输出左子结点——>根节点——>右子节点

public void minOrder(TreeNode root)
{
    if(root==null)
         return;
    else{
        minOrder(root.left);
        System.out.println(root.val+" ");
        minOrder(root.right);
}

后序遍历：左子结点——>右子节点——>根节点

public void BehindOrder(TreeNode root)
{
    if(root==null)
         return;
    else{
        BehindOrder(root.left);
        BehindOrder(root.right);
        System.out.println(root.val+" ");
}

层序遍历：从所在二叉树的根节点出发，首先访问第一层的树根节点，然后从左到右访问第二层的节点，以此例推，自上而下，自左至右逐层访问

           设计思想：层序遍历最好的解决方法就是队列。首先将二叉树的根节点放入队列中；然后进入循环（循环的掉件就是队列不为空），去寻找队列中对头元素的左节点和右节点是否存在，若存在则将其添加到队尾，同时弹出对头元素

在这里我们需要再学习一下队列的有关基本操作

压入元素(添加)：add()、offer()
相同：未超出容量，从队尾压入元素，返回压入的那个元素。
区别：在超出容量时，add()方法会对抛出异常，offer()返回false

弹出元素(删除)：remove()、poll()
相同：容量大于0的时候，删除并返回队头被删除的那个元素。
区别：在容量为0的时候，remove()会抛出异常，poll()返回false

获取队头元素(不删除)：element()、peek()
相同：容量大于0的时候，都返回队头元素。但是不删除。
区别：容量为0的时候，element()会抛出异常，peek()返回null。
原文链接：https://blog.youkuaiyun.com/Archiea/article/details/122512483

public void levelOrder(TreeNode root){
   if(root==null) return;
   //创建队列
   Queue<TreeNode> queue=new LinkenList<>();
   queue.offer(root);   //将根节点压入队
   while(! queue.isEmpty()){
       if(queue.peek().left!=null)
           queue.offer(queue.peek().left);  //队头元素的左节点存在，则将其入队
       if(queue.peek().right!=null)
           queue.offer(queue.peek().right);//队头元素的右节点存在，则将其入队
       queue.poll();//将队头元素删除
    }
}

2、求树的最大深度

   这也是本题的要求，我们之前说过要解决二叉树相关的题目，一般都需要使用递归的思想；此题是要求最大深度，即左子树的最大深度或右子树的最大深度；

   思路：若root==null return 0；否则；访问左子树的最大深度+1;访问右子树的最大深度+1；最后返回最大的值

public int maxDepth(TreeNode root){
 
   if(root==null)
      return 0;
   else{
     int left=maxDepth(root.left)+1;  //访问左子树+1（+1是因为已确定此时根节点存在）
     int right=maxDepth(root.right)+1;//访问右子树+1
     return left>right? left: right);
}

3、求第n层的节点数

思路：若此时root==null return null; 若n==1,直接返回root 否者返回左子树(k-1)层+右子树（k-1）层

public int getKLevel(TreeNode root,int k)
{
    if(root==null)
       return 0;
    elseif(n==1)
       return 1;
    else{
       return getKLevel(root.left,k-1)+getKLevel(root.right,k-1);
    }
}