计算机组成原理定点运算-移位、加、减、乘、除（详细解析-看完就会）

最新推荐文章于 2024-01-13 12:19:10 发布

原创

最新推荐文章于 2024-01-13 12:19:10 发布 · 2.5w 阅读

225 ·

CC 4.0 BY-SA版权

本网站/论坛/博客为编辑作品，整体著作权属于本人（筱楠）所有。本网站/论坛/博客许可他人建立友情链接，但链接所指向的内容应是本网站/论坛/博客首页。未经本人许可不得随意转载

本文深入解析定点运算，包括移位运算的原理与应用，加法、减法、乘法及除法的具体运算规则，以及溢出判断的方法。通过实例演示了各种运算的执行过程，适合计算机科学领域的学习者。

定点运算

一、移位运算

1.移位运算的意义：

计算机中的移位是数据相对于小数点移位（左移或右移），数据移动，小数点位置不发生变化

2.在平常，数值移位

左移：绝对值扩大
右移：绝对值缩小

3.在计算机中二进制移位

左移：数值绝对值变为原来2倍
右移：数值绝对值变为原来1/2倍

4.算术移位规则

有符号位的移位

左移1位：机器数对应真值的绝对值变为原来2倍
右移1位：机器数对应真值的绝对值变为原来1/2倍

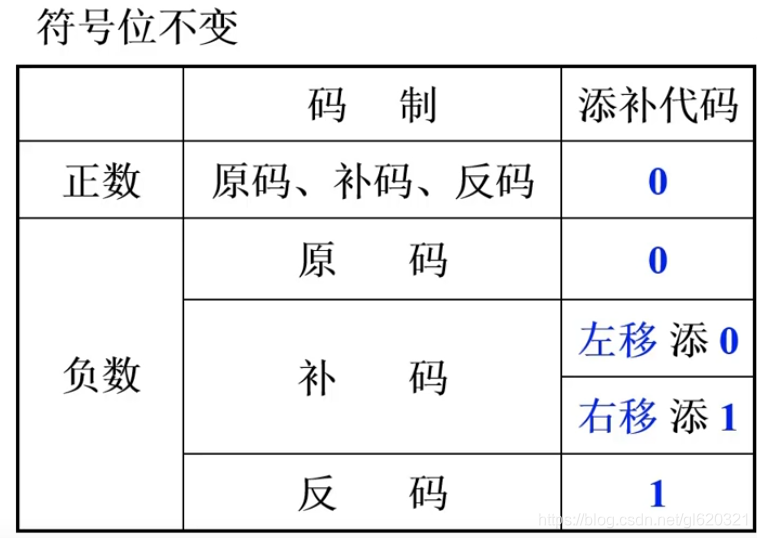
5.移位过程中，如何填补空位

负数：数值部分和真值相同
在这里插入图片描述

6.逻辑移位与算术移位

无符号数的移位

逻辑左移低位添0，高位移丢
逻辑右移高位添0，低位移丢

例如：
01010011
逻辑左移所有位都参加移位操作高位0移丢，最低位添0 ：10100110
算术左移第一个0表示符号位，这个数为正数，符号位不参与移位，移位的是后面的数据00100110

例如：
10110010
逻辑右移所有位都参加移位操作空出的最高位补0，最低位丢弃01011001
算术右移最高位不参与移位，符号位，表示负数，右移左侧空出最高位添1，右侧0丢弃11011001

二、加法和减法运算

1.补码加减法运算公式
在计算机中
（1）加法
A+B整数：【A】补+【B】补=【A+B】补（mod 2^(n+1)）
A+B小数：【A】补+【B】补=【A+B】补（mod 2）

（2）减法: A-B=A+(-B)
A-B整数：【A-B】补=【A+（-B）】补（mod 2^(n+1)）
A-B小数：【A-B】补=【A+（-B）】补（mod 2）

补码运算：连同符号位一起相加，符号位产生的进位自然丢掉

加法例题：
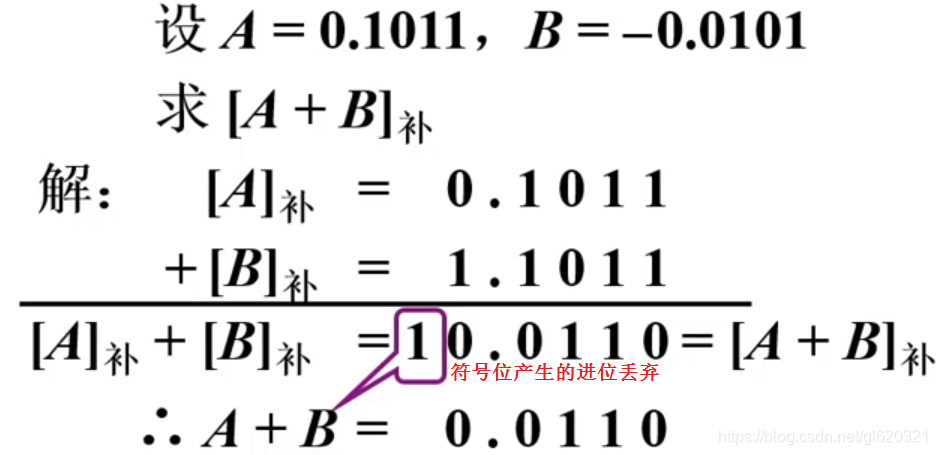
在这里插入图片描述

最低0.47元/天解锁文章

6 条评论

星小海 2022.11.05
问一下对于加法的溢出判断如果是 A=0,0000111(7), B=1,1111011(-5) ，求A+B=? 这个时候结果是10,0000010，那这个异或运算不应该是1XOR0 结果是1吗？可是这个也没有溢出呢？
- 星小海回复星小海 2022.11.06
  懂了，是最高有效位的进位，而不是最高有效位，这里符号位进位为1，最高有效位为0，但是最高有效位的进位为1，1XOR1=0，所以没有溢出。

ax6808 2022.06.19
哇! 厉害了我的哥!深入浅出,云里雾里! 开始KEIL C51公式中好像无符号整数才能移位乘除,不然告警..后来有个32位定点公式里各种变量都有,居然都能用左右移位法..又搞糊涂了: s32 adc_T, adc_P, t_fine, var1, var2, T; //ok; 32位定点公式用; u32 p; //ok; 32位定点公式用; u16 dig_T1, dig_P1; //ok,2个无符号,其余10个有符号; s16 dig_T2, dig_T3, dig_P2, dig_P3, dig_P4, dig_P5, dig_P6, dig_P7, dig_P8, dig_P9; var1 = ( ( ((adc_T>>3) - ((s32)dig_T1<<1)) ) * ((s32)dig_T2) )>>11; var2 = (((((adc_T>>4) - ((s32)dig_T1)) * ((adc_T>>4) - ((s32)dig_T1)))>>12) *((s32)dig_T3))>>14; t_fine = var1 + var2; T = (t_fine * 5 + 128)>>8; var1 = (((s32)t_fine)>>1) - (s32)64000; var2 = (((var1>>2) * (var1>>2))>>11) * ((s32)dig_P6); var2 = var2 + ((var1*((s32)dig_P5))<<1); var2 = (var2>>2)+(((s32)dig_P4) <<16); var1 = (((dig_P3 * (((var1>>2) * (var1>>2))>>13))>>3) + ((((s32)dig_P2) * var1)>>1))>>18; var1 =((((32768+var1))*((s32)dig_P1))>>15); p = (((u32)(((s32)1048576)-adc_P)-(var2 >> 12)))*3125; ..........
- ax6808回复ax6808 2022.06.19
  我的笔记摘录: 注意:切勿混用带符号类型和无符号类型:注意溢出错误系统不提示! 变量:整型、实型、字符型; 自定义(typedef声明只是改名好记而已!); (1)Keil MDK针对32位单片机:int4字节,double8字节; (2)Keil 51 针对 8位单片机:int2字节,double4字节;简化为int=short,double=foat7位十进制有效数字,无8字节：已明确! 运算:运算中C51允许任何标准数据类型隐式转换,优先级顺序：Bit→char→int→long→float→signed→unsigned; 支持一些复杂组合型数据类型:数组、指针、结构、联合等; 注意:有符号及无符号混合运算规则,可强制转换; 注意:无符号变量才能移位?,左移不够位时要扩展(强制转换); 奇怪了:32位定点公式里全部都能用左右移位? 注意:运算符优先级:算术>移位>条件>按位>逻辑>赋值... 不清楚最好加(); 浮点数和补码表示的定点数的表示范围有所不同，定点数连续，而浮点数可能不连续。....
- ax6808回复ax6808 2022.06.19
  是不是上面只涉及"定点运算-移位、加、减、乘、除",所以才可以? 我之前的有浮点变量的运算就要强制转换一些变量数据类型才能正常运算? 好多公式只能先抄再一步步调试......变量的具体类型定义和存储具体格式跟串口显示格式几乎两回事,有联系. 我依然似懂非懂...搞了很久...谢谢!