深度优先遍历（DFS）- Letter CasePermutation - Combinations

深度优先遍历（DFS）

思路：从图中一个未访问的顶点V开始，沿着一条路一直走到尽头，然后从这条路尽头的节点回退到上一个节点，再从另一条路开始走到尽头…,不断递归重复此过程，直到所有顶点都遍历完成。

特点：不撞南墙不回头，先走完一条路，再换另一条路，继续走，和数的前序遍历一样

树的深度优先遍历

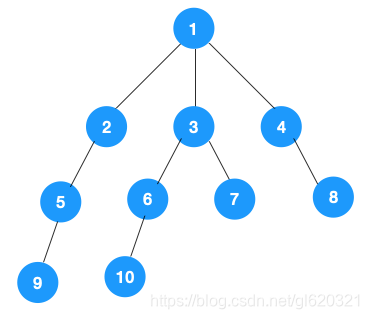
1.从根节点1开始遍历，它的子节点有2,3,4，先遍历节点2，再遍历节点5，之后遍历节点9.

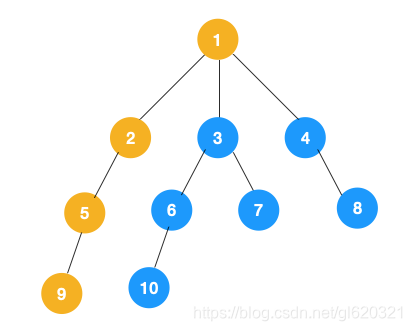
2.第一条路已经走到底了，9是叶子节点，没有子节点，从9回退到节点5，看节点5是否还有没有遍历的节点，若没有，继续回退，回退到节点2,节点2还是没有未遍历的节点，继续回退，回退到根节点1。
发现根节点1有两个未遍历的子节点3和4，选择节点3，继续向下遍历，

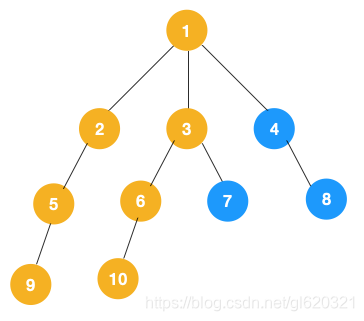
和步骤2一样，一条路遍历到最后一个叶子节点10，开始回退，回退到6，继续回退到3，发现节点3未遍历，此时遍历节点7.

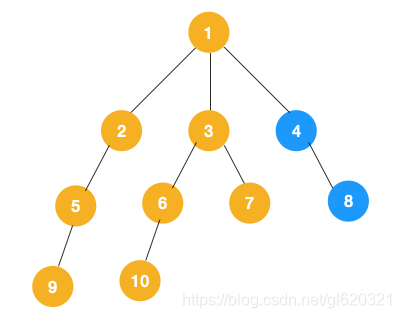
从节点7回退，回退到节点3，再回退到根节点1，选择未遍历的子节点4，一直往下遍历，依次遍历节点4，节点8.

完整节点的遍历顺序：1,2,5,9,3,6,10,7,4,8

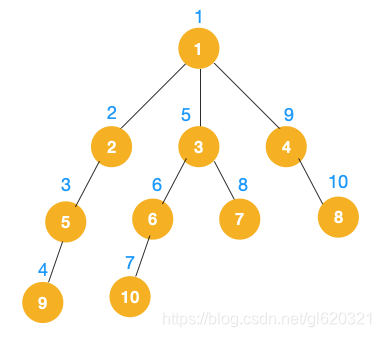
综上所述：就会发现树的深度优先遍历就是数的前序遍历

递归实现：前序遍历（根节点，左节点，右节点）

---

1.题目：Letter CasePermutation

• English

Given a string S, we can transform every letter individually to be lowercase or uppercase to create another string. Return a list of all possible strings we could create.

Examples:
Input: S = “a1b2”
Output: [“a1b2”, “a1B2”, “A1b2”, “A1B2”]

Input: S = “3z4”
Output: [“3z4”, “3Z4”]

Input: S = “12345”
Output: [“12345”]

Note:
S will be a string with length at most 12.
S will consist only of letters or digits.

• 中文：

给定一个字符串S，我们可以将每个字母分别转换为小写或大写以创建另一个字符串。返回我们可以创建的所有可能字符串的列表。

示例：
输入：S=“a1b2”
输出：[“a1b2”，“a1B2”，“A1B2”，“A1B2”]

输入：S=“3z4”
输出：[“3z4”，“3Z4”]

输入：S=“12345”
输出：[“12345”]

注：
S将是一个长度不超过12的字符串。
S将仅由字母或数字组成。

---

• 分析思路：
  由于输入的字符串中只有字母和数字，小写字母的ASCll码范围是：97~ 122，大写字母的ASCll码范围是：65~ 90，数字字符的范围是：49~57。观察到数字字符的ascll码比字母都要小而且小写字母比对应的大写字母大32，采用异或32刚好是2的32次方，所以相当于小写字母的二进制表示ASCll码从右往左的第6位由0变成1就变成了对应的大写字母同理对于大写字母把第六位的1变成0就是大写向小写的转换，这个过程可以用S[i]^32来完成。

• 代码：

class Solution{
public:
	vector<string> ans; //全局变量
	vector<string> letterCasePermutation(string S){
		dfs(S,0); //搜索所有字符串和当前位 
		return ans;
	}
	void dfs(string S,int u){ //传字符串与当前枚举到第几位 
		if(u==S.size())
		{
			ans.push_back(S);
			return;
		}
		dfs(S,u+1);//当前位不变 
		if(S[u]>='A')//若是字母 
		{
			S[u]^=32; //大写变小写，异或32 ASII：A=65，a=97 
			dfs(S,u+1);
			int main(){
				
			} 
		}
	}
};

---

2.题目：Combinations

English：

Given two integers n and k, return all possible combinations of k numbers out of 1 … n.

For example,
If n = 4 and k = 2, a solution is:

[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]

中文：

给定两个整数n和k，返回1中k个数的所有可能组合…n。

例如，

如果n=4，k=2，则解为：
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]

---

• 分析思路：

搜组合数（保证不重不漏），从前往后排列1,2,3…n从前往后看每个数是不是要选，从前往后选k个数，保证所选的次序是有序的，从前往后选（从小到大），这样就不用再去考虑顺序问题，因为选好的数都是按顺序排列好的，（顺序不会导致产生新的方案，不会重复)

• 代码：

class Solution{
public:
	vector<vector<int> > ans;  //全局变量 
	vector<vector<int> > combine(int n,int k){
		vector<int> path;  //方案 
		dfs(path,1,n,k); //传参，方案，1-n，k：需要选的数 
		return ans;
	}
	void dfs(vector<int> &path,int start,int n,int k) //start：当前可选起始位置，n：总数，k：当前需要选的数 
	{
	if(!k){  //出口条件，不需要选任何数 
		ans.push_back(path); //加入计数中 
		return; 
	}
	for(int i=start;i<=n;i++) //可选起始位置 
	{
		path.push_back(i); //更新状态 ，加入i 
		dfs(path,i+1,n,k-1); //递归搜索 ，当前数为i，所以下一个可选数为i+1（保证选得数从小到大），剩余选k-1个数 
		path.pop_back();//回溯，恢复现场，前面加入i，在此处把最后一个元素删掉 
	}
	}
};