第二套3344

1.卡片

思路：枚举
2.直线

思路：枚举，浮点数判断
3.货物摆放

思路：把n质因数分解掉，可以发现是有5个质因子是一次，一个质因子是三次
所以答案是3的5次方再乘以10.这里只给出求唯一分解的代码。

void mPrime(long long int x)
{
    printf("%lld = ", x);
    for (long long int i = 2; i * i <= x; i++)
    {
        if (x % i == 0)
        {
            int num = 0;
            while (x % i == 0)
            {
                x /= i;
                num++;
            }
            primeNum.push_back(num);
            primeVal.push_back(i);
        }
    }
    if (x > 1)
    {
        primeNum.push_back(1);
        primeVal.push_back(x);
    }

    for (unsigned int i = 0; i < primeNum.size(); i++)
    {
        if (i != 0)
        {
            printf("  *  ");
        }
        printf("\n(%lld ^ %lld)", primeVal[i], primeNum[i]);
    }
    printf("\n");
}

4.路径

思路：
共2021个结点组成的图，枚举任意两点组合，通过计算最大公约数，记录这两个点之间的距离，即增加一条边。然后floyd跑最短路。

#include <iostream>
#include <vector>
#include <algorithm>
#include <cstring>
using namespace std;
const int maxn = 2021;
vector<int> u[maxn + 52];
vector<int> v[maxn + 52];
int disDijk[maxn + 52];
int disFloyd[maxn + 52][maxn + 52];
bool vis[maxn + 52];
void InitGroup()
{
    for (int i = 1; i <= maxn; i++)
    {
        for (int j = i + 1; j <= maxn; j++)
        {
            if (j - i <= 21)
            {
                u[i].push_back(j);
                v[i].push_back(i * j / __gcd(i, j));
                u[j].push_back(i);
                v[j].push_back(i * j / __gcd(i, j));
            }
        }
    }
}
void Floyd()
{
    memset(disFloyd, 0x3f, sizeof(disFloyd));
    for (unsigned int i = 1; i <= maxn; i++)
    {
        for (unsigned int j = 0; j < v[i].size(); j++)
        {
            disFloyd[i][u[i][j]] = v[i][j];
            disFloyd[u[i][j]][i] = v[i][j];
        }
    }
    for (int k = 1; k <= maxn; k++)
    {
        for (int i = 1; i <= maxn; i++)
        {
            for (int j = 1; j <= maxn; j++)
            {
                disFloyd[i][j] = disFloyd[j][i] = min(disFloyd[i][j], disFloyd[i][k] + disFloyd[k][j]);
            }
        }
    }
    printf("%d\n", disFloyd[1][maxn]);
}
int main()
{
    InitGroup();
    Floyd();
    return 0;
}

5.空间

思路：直接算

6.砝码称重

思路：
用动态规划
状态定义： d p ( i , j ) 表示前 i 个数字选择若干个加或者减，能否获得和为 j 。
状态转移方程： d p ( i , j ) = d p ( i − 1 , j ) ∣ d p ( i − 1 , j − a [ i ] ) ∣ d p ( i − 1 , j + a [ i ] )
初始状态： d p ( 0 , 0 ) = 1 。
（要开滚动数组）

#include <bits/stdc++.h>
using namespace std;
const int offset = 100052;
const int maxn = 100052 + offset;
int n, vis[2][maxn], a[2000];
int main()
{
    scanf("%d", &n);
    for (int i = 0; i < n; i++)
    {
        scanf("%d", &a[i]);
    }
    memset(vis, 0, sizeof(vis));
    vis[0][offset] = 1;
    int pre = 0, cur = 1;
    // 三种情况分别是，不选择a[i]，选择a[i]，选择-a[i]
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < maxn; j++)
        {
            vis[cur][j] = max(vis[cur][j], vis[pre][j]);
            if (j - a[i] >= 0)
            {
                vis[cur][j] = max(vis[pre][j - a[i]], vis[cur][j]);
            }
            if (j + a[i] < maxn)
            {
                vis[cur][j] = max(vis[pre][j + a[i]], vis[cur][j]);
            }
        }
        swap(pre, cur);
    }
    int ans = 0;
    for (int i = offset + 1; i < maxn; i++)
    {
        if (vis[pre][i])
        {
            ans++;
        }
    }
    printf("%d", ans);
    system("pause");
    return 0;
}

7.括号序列

思路：动态规划
状态定义： d p ( i , j )表示前 i 个括号插入若干个括号之后，左括号比右括号多 j 个的插入方法数。
状态转移方程：
d p ( i , j ) = d p ( i − 1 , j − 1 ) （stri是左括号），

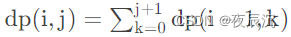
初始状态： d p ( 0 , 0 ) = 1

#include <bits/stdc++.h>
using namespace std;
const int maxn = 5052;
const long long int MOD = 1e9 + 7;
int dp[maxn][maxn];
bool vis[maxn][maxn];
char str[maxn];
int n;
long long int mod(long long int x) { return x % MOD; }
long long int GetAns() {
  memset(dp, 0, sizeof dp);
  memset(vis, 0, sizeof vis);
  dp[0][0] = 1;
  vis[0][0] = true;
  for (int i = 1; i <= n; i++) {
    if (str[i - 1] == '(') {
      for (int j = 1; j <= n; j++) {
        dp[i][j] = dp[i - 1][j - 1];
        vis[i][j] = vis[i - 1][j - 1];
      }
    } else {
      dp[i][0] = mod(dp[i - 1][0] + dp[i - 1][1]);
      vis[i][0] = vis[i-1][0] | vis[i-1][1];
      for (int j = 1; j <= n; j++) {
        dp[i][j] = mod(dp[i - 1][j + 1] + dp[i][j - 1]);
        vis[i][j] = vis[i - 1][j + 1] | vis[i][j - 1];
      }
    }
  }
  for (int i = 0; i <= n; i++) {
    if (vis[n][i] != 0) {
      return dp[n][i];
    }
  }
  return -1;
}
int main() {
  scanf("%s", str);
  n = strlen(str);
  long long int ansL = GetAns();
  reverse(str, str + n);
  for (int i = 0; i < n; i++) {
    if (str[i] == ')') {
      str[i] = '(';
    } else {
      str[i] = ')';
    }
  }
  long long int ansR = GetAns();
  printf("%lld\n", mod(ansL * ansR));
  system("pause);
  return 0;
}

8.时间显示

思路：
一天包含24 * 60 * 60 * 1000毫秒
扣除整天的描述之后，得到最后一天剩下了多少毫秒
忽略毫秒，得到还剩多少秒
一小时3600秒，走过了多少个完整的3600秒就代表当前小时数是多少
走完全部的完整60秒之后剩下的秒数就是秒数

#include <bits/stdc++.h>
using namespace std;
int main()
{
    int t;
    cin >> t;
    long long int dayMs = 24 * 60 * 60 * 1000; 
    while (t--)
    {
        long long int n;
        scanf("%lld", &n);
        n = n % dayMs;
        n = n / 1000;
        int hour = n / (3600);
        int minutes = (n - hour * 3600) / 60;
        int second = n % 60;
        printf("%02d:%02d:%02d\n", hour, minutes, second);
    }
    return 0;
}

9.杨辉三角形

思路：根据杨辉三角特性，总结出公式：

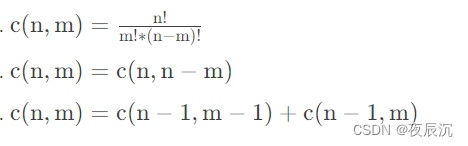
c(n,m)指的是第n行第m个数。

每一行是对称的，所以如果如果一个数字在某一行的右半边出现，那么它一定也在这一行的左半边出现，因此每一行右半边的数字一定不会作为第一个出现的数字。

最后在前20列对于每一列搜索是否有这个数的存在。

// 杨辉三角
#include <bits/stdc++.h>
using namespace std;


// 二分方法
long long int n;
long long int C(long long int a, long long int b)
{
    long long int ret = 1;
    for (long long int i = a, j = 1; j <= b; i--, j++)
    {
        ret = ret * i / j;
        if (ret > n)
        {
            return n + 1;
        }
    }
    return ret;
}
long long int GetAns(int col)
{
    long long int l = col, r = max(n, (long long int)col);
    while (l < r)
    {
        long long int mid = (l + r) / 2;
        if (C(mid, col) >= n)
            r = mid;
        else
            l = mid + 1;
    }
    if (C(r, col) != n)
    { // 没有出现则返回出现位置无限大
        return 4e18;
    }
    else
    {
        return r * (r + 1) / 2 + col + 1;
    }
}

int main()
{
    scanf("%lld", &n);

    long long int ans = 4e18;
    for (int i = 0; i < 20; i++)
    { 
        long long int cur = GetAns(i);
        ans = min(ans, cur);
    }
    printf("%lld\n", ans);
   	//system("pause");
    return 0;
}

10.双向排序

思路：硬模拟的，用sort，连续的0操作或者1操作，只需要执行覆盖数组长度最长的操作，这样可以优化一点，（应该考虑用线段树）

#include <bits/stdc++.h>
using namespace std;
const int maxn = 100052;
int a[maxn];
bool cmp(int x, int y) { return x > y; }
struct Oper {
  int pos, op;
};
int main() {
  int n, m;
  scanf("%d%d", &n, &m);
  for (int i = 0; i < n; i++) {
    a[i] = i + 1;
  }
  // 读取操作列表
  vector<Oper> opList;
  for (int i = 0; i < m; i++) {
    Oper temp;
    scanf("%d%d", &temp.op, &temp.pos);
    opList.push_back(temp);
  }
  // 连续的0操作或者1操作，只需要执行覆盖数组长度最长的操作(去重)
  vector<Oper> newList;
  Oper curOp = opList[0];
  for (unsigned int i = 0; i < opList.size(); i++) {
    if (curOp.op != opList[i].op) {
      newList.push_back(curOp);
      curOp = opList[i];
      continue;
    }
    if (opList[i].op == 0 && opList[i].pos > curOp.pos) {
      curOp = opList[i];
    }
    if (opList[i].op == 1 && opList[i].pos < curOp.pos) {
      curOp = opList[i];
    }
  }
  newList.push_back(curOp);
  // 模拟执行操作
  for (unsigned int i = 0; i < newList.size(); i++) {
    if (newList[i].op == 0) {
      sort(a, a + newList[i].pos, cmp);
    } else {
      sort(a + newList[i].pos - 1, a + n);
    }
  }
  for (int i = 0; i < n; i++) {
    if (i != 0) {
      printf(" ");
    }
    printf("%d", a[i]);
  }
  return 0;
}