cpp源码STL之vector中push_back的时间复杂度分析

最新推荐文章于 2024-07-19 22:42:53 发布
原创 最新推荐文章于 2024-07-19 22:42:53 发布 · 773 阅读 · 2 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文分析了一种数据结构在连续操作中的时间复杂度变化，特别是插入操作时从最好O(1)到最坏O(n)的变化，并通过实例推导出均摊复杂度为O(1)。讨论了在内存不足时重新分配内存对复杂度的影响。

先说结论

最好是O(1)，最差是O(n), 均摊是O(1)。

最好的情况，就是插入的时候，还有空余；最坏的情况，就是每次插入都满了，要重新分配内存。

均摊复杂度，先看一下定义

对一个数据结构进行一组连续操作中，大部分情况下时间复杂度都很低，只有个别情况下时
间复杂度比较高，而且这些操作之间存在前后连贯的时序关系，这个时候，我们就可以将这
一组操作放在一块儿分析，看是否能将较高时间复杂度那次操作的耗时，平摊到其他那些时
间复杂度比较低的操作上。

推导

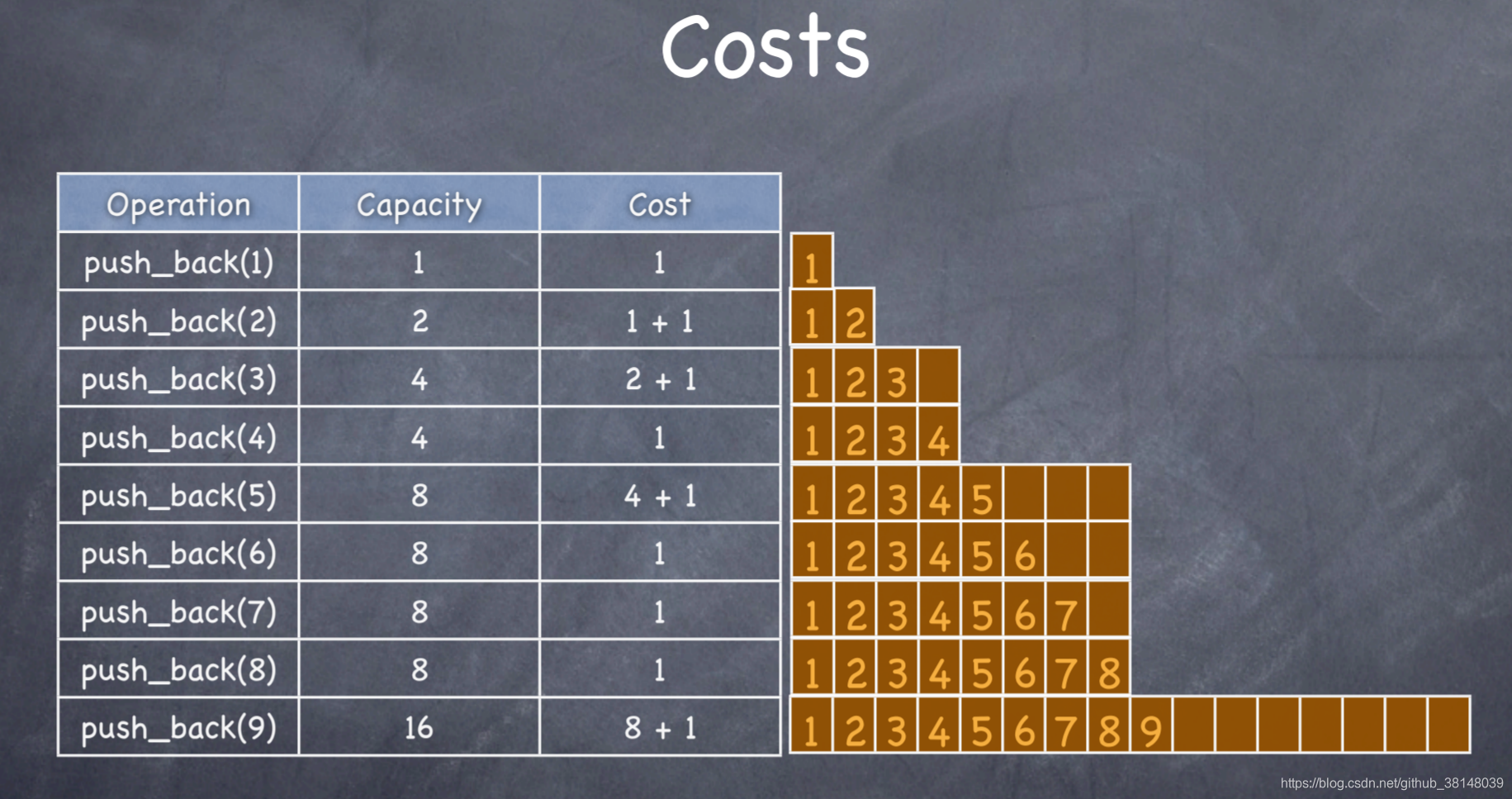
在这里插入图片描述

在这里插入图片描述

这里就是按照定义，对插入九个数的过程进行了分析，其中当插入的空间不够时，会重新分配两倍的大小内存，详细解释，查看参考博客。

其中，不等号是进行了缩放，假设全部数量为１，然后有logn次的重新分配内存。

对等比数列求和使用了公式，
在这里插入图片描述

参考博客：
求和公式
tamu大学的教育课件
STL中push_back的详细过程
push_back源码剖析

关于stl中vector的push_back的探究
jibi3778的博客
05-15 413
面试中被问到vector的内存增长方式是否自己试过，十分羞愧只是道听途说，之后在博客上看到了一些源码分析才有所了解，以下内容转载部分为网址形式，个人实验内容贴出细节，转载部分侵权删。 push_back的源码解析： https://blog.youkuaiyun.com/cxc576502021/article/details/83020617 之后是我关于push_back的自己试验，实验发现，我使用的版本push_back是1.5倍增长的，并不是网上说的两倍，不过这个看源码应该是可以改动的系数，贴上我的实验图片和代
c++中emplace_back()与push_back()的区别，STL，vector，list，map
qq_35102059的博客
10-13 1524
emplace_back() 和 push_back() 的区别，就在于底层实现的机制不同。 push_back() 向容器尾部添加元素时，首先会创建这个元素，然后再将这个元素拷贝或者移动到容器中（如果是拷贝的话，事后会自行销毁先前创建的这个元素)。使用到了拷贝构造函数。 而 emplace_back() 在实现时，则是直接在容器尾部创建这个元素，省去了拷贝或移动元素的过程。直接使用构造参数列表来添加元素的方法，它会使用到了移动构造函数 move（不用拷贝一个复制品）。 源码实现的区别： _A
c++：vector的push_back时间复杂度分析
zzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzz
02-17 4094
vector是如何增长的： 为了支持快速随机访问，vector是连续存储的。 当添加一个新元素时，如果没有空间容纳新元素，为了保持连续存储，容器必须分配新的内存空间保存已有元素和新元素。 转移流程：申请新空间，转移元素，释放旧空间。 为了避免每次添加元素都需要转移一次空间，当需要扩容时，vector会申请一个比需求更大的内存空间，即预留一部分空间作为备用。 push_back复杂度分析： push_back均摊后的时间复杂度为O(1)。 vector只有当达到capacity之后才会扩容。 设倍增因子为m.
vector中push_back()的时间复杂度（字节一面）
qq_46780256的博客
12-19 3375
vector中push_back()的原理： 当容器的大小达到容量后，为了保证内存的连续性，就会再开一个新的内存块，把之前的数据复制过去。 每次复制的时间复杂度是O(n)，每次push_back的时间复杂度不太像O(1)，但由于只有很少的情况下才会复制，所以均摊的时间大约是O(1)。 #include<iostream> #include<vector> using namespace std; int main() { vector<int> v; int
vector push_back 时间复杂度
neninee的博客
11-03 1436
#include <iostream> #include <vector> using namespace std; int main(){ vector<int> vec; int last = 0; for(int i = 0; i <= 1e5; i++){ vec.push_back(1); if(last!=(int)vec.capacity()){ c
vector push_back 时间复杂度分析
Bob__yuan的博客
10-19 5168
  《C++程序设计语言》第4部分：标准库，里边写 vector，第一句如下： The STL vector is the default container. Use it unless you have a good reason not to. If your suggested alternative is a list or built-in array, think twice. ...
push_back时间复杂度
a13602955218的博客
03-23 796
http://blog.sina.com.cn/s/blog_973657a00102x41w.html
C++ vector中push_back与emplace_back性能对比解析
在C++标准模板库（STL）中，`std::vector` 是最常用且最重要的容器之一，用于动态管理连续内存中的对象序列。随着C++11标准的引入，`std::vector` 新增了 `emplace_back` 成员函数，与原有的 `push_back` 形成对比。...
vector1_STL_C++_vector_
10-02
STL中的`vector`是其中一个核心容器，它允许程序员动态地存储、管理和操作一组同类型的元素。`vector`在功能上类似于动态数组，具有方便的内存管理以及高效的操作性能。 ### `vector`的基本概念 `vector`是一个...
C++容器中push_back与emplace_back性能对比分析
随着C++11标准的发布，STL容器引入了许多新的成员函数以提升性能与编程效率，其中`emplace_back`与传统的`push_back`之间的差异成为现代C++开发中一个关键且值得深入探讨的话题。本文将围绕“C++容器中`push_back`与...
vector中push_back的复杂度
qq_35429629的博客
03-27 1034
问题： 将N个元素使用push_back插入到vector中， 求push_back操作的复杂度。 简单分析如下： 考虑vector每次内存扩充两倍的情况。 如果我们插入N个元素， 则会引发lgN次的内存扩充，而每次扩充引起的元素拷贝次数为 2^0, 2^1, 2^2, ..., 2^lgN. 把所有的拷贝次数相加得到 ...
【时间复杂度分析】将N个元素使用push_back插入到vector中， 求push_back操作的复杂度
喜欢吃冰棍de谷利文君的博客
06-12 1115
转自：问题： 将N个元素使用push_back插入到vector中， 求push_back操作的复杂度。 参考：C++ std::vector中push_back操作时间复杂度分析 分析如下： 考虑vector每次内存扩充两倍的情况： 如果我们插入N个元素，则会引发lgN次的内存扩充，而每次扩充引起的元素拷贝次数为 20,21,22,...,2lgN.2^0, 2^1, 2^2,...,2^{lgN}. 20,21,22,...,2lgN. 为什么是lgN次的内存扩充？ 如下表所示： 元素个数
问题： 将N个元素使用push_back插入到vector中， 求push_back操作的复杂度。
轻锋的专栏
09-23 8084
简单分析如下：     考虑vector每次内存扩充两倍的情况。     如果我们插入N个元素， 则会引发lgN次的内存扩充，而每次扩充引起的元素拷贝次数为                                       2^0,  2^1, 2^2, ..., 2^lgN.     把所有的拷贝次数相加得到                     2^0
初始vector为空，那么push_back N次时间复杂度多少
richardzrc的博客搬家了--->richardzhang.info
07-12 2888
总结： 好像没有设置vector的capabilities的方法，都是系统自动分配的。所以如果一开始设置容量下的话，一直resize，搬元素效率很低。具体未必为两倍，如果当成两倍的话。 题目解答：如果初始vector为空，那么push_back N次时间复杂度多少？ 假设容量每次是之前两倍的扩充的话，实际我测VS2010好像不是两倍的，就拿1,2,3.。。10这么算，容量扩充序列是1,
揭秘vector的魔法：push_back()的均摊O(1)复杂度之谜
最新发布
m0_72877724的博客
07-19 754
vector的push_back()操作展示了计算机科学中一个有趣的现象：通过巧妙的设计，我们可以在保持高效率的同时提供方便的接口。虽然单次push_back()操作的时间复杂度可能是O(n)，但从长期来看，它的均摊复杂度却是O(1)。当空间不足时，vector会重新分配一个更大的内存块，并将所有元素复制到新的位置。通常，每次需要扩容时，新的容量会是原来的1.5倍或2倍。均摊分析考虑的是一系列操作的平均成本，而不是单个操作的最坏情况。因此，n次操作的总成本小于3n，平均每次操作的成本小于3，即O(1)。
数组01 Vector中的push_back[C++]
weixin_42789937的博客
01-18 4590
上机题目练习整理，本篇作为线性表的代码补充，提供了两种（差别并不大）算法，供小伙伴们参考~🥝🥝
数据结构与算法 C++关键字 Vector
Android驱动开发
10-19 998
Vector函数功能 1.push_back 在数组的最后添加一个数据 2.pop_back 去掉数组的最后一个数据 3.at 得到编号位置的数据 4.begin 得到数组头的指针 5.end 得到数组的最后一个单元+1的指针 6.front 得到数组头的引用 7.back 得到数组的最后一个单元的引用 8.max_size 得到vector最大可以是多大 9.capacity 当前vector分配的大小 10.size 当前使用数据的大小 11.resize 改变当前使用数据的大小，如果它比当前使用的大，
C++：vector的push_back()与emplace_back()
天启的博客
07-28 6055
在STL中，向vector容器添加元素的函数有2个：push_back()、emplace_back() 1.push_back() 在vector容器尾部添加一个元素，用法为： arr.push_back(val); 2.emplace_back() C++11新增，功能与push_back相同，向vector容器尾部添加一个元素，用法为： arr.emplace_back(value); 3.区别 可以发现push_back()与empl...
评论
成就一亿技术人!
拼手气红包6.0元
还能输入1000个字符
 
红包 添加红包
表情包 插入表情
表情包 代码片
 条评论被折叠 查看
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值