看了这个解释，终于明白线性回归模型了

 

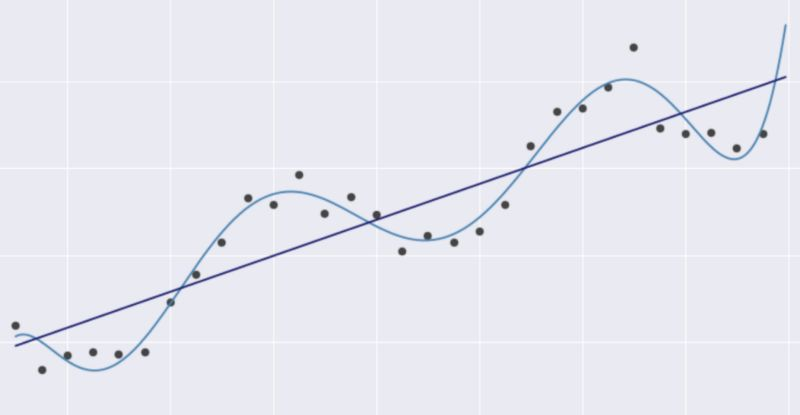
在机器学习和统计领域，线性回归模型是最简单的模型之一。这意味着，人们经常认为对线性回归的线性假设不够准确。

 

例如，下列2个模型都是线性回归模型，即便右图中的线看起来并不像直线。

 

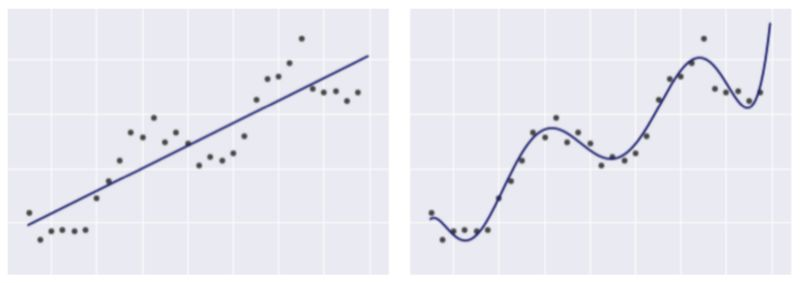
图1 同一数据集的两种不同线性回归模型

 

若对此表示惊讶，那么本文值得你读一读。本文试图解释对线性回归模型的线性假设，以及此类线性假设的重要性。

 

回答上述问题，需要了解以下两个简单例子中线性回归逐步运行的方式。

 

例1：最简单的模型

 

从最简单的例子开始。给定3对（x，y）训练数据：（2,4）、（5,1）、（8,9）进行函数建模，发现目标变量y和输入变量x之间的关系。

 

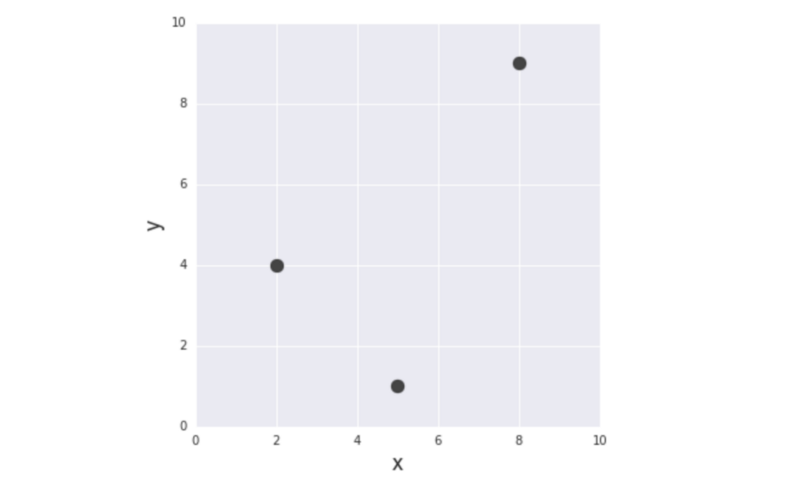
图2 本文中使用的训练数据集

 

这一模型最为简单，如下所示：

 

 

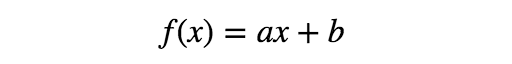
通过运用该简单的线性函数，可模拟x和y之间的关系。关键在于该函数不仅与输入变量x成线性关系，而且与参数a、b成线性关系。

 

当前目标是确定最符合训练数据的参数a和b的值。

 

这可通过测量每个输入x的实际目标值y和模型f（x）之间的失配来实现，并将失配最小化。这种失配（=最小值）被称为误差函数。

 

有多种误差函数可供选择，但其中最简单的要数RSS，即每个数据点x对应的模型f（x）与目标值y的误差平方和。

 

 

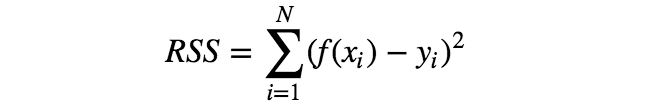
利用误差函数的概念，可将“确定最符合训练数据的参数a、b”改为“确定参数a、b，使误差函数最小化”。

 

计算一下训练数据的误差函数。

 

 

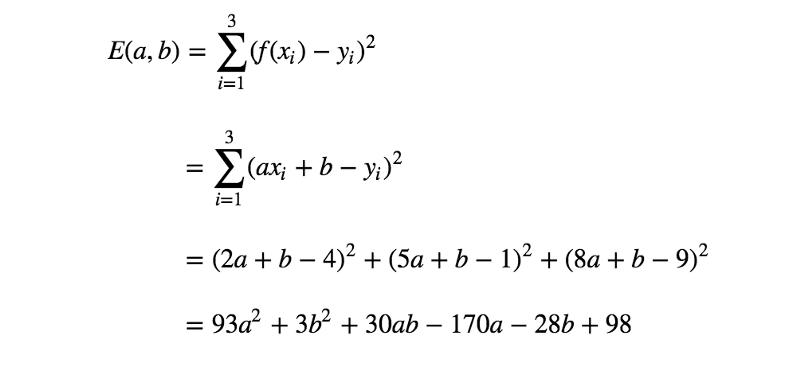
上面的等式就是要求最小值的误差函数。但是，怎样才能找到参数a、b，得到此函数的最小值呢？为启发思维，需要将该函数视觉化。

 

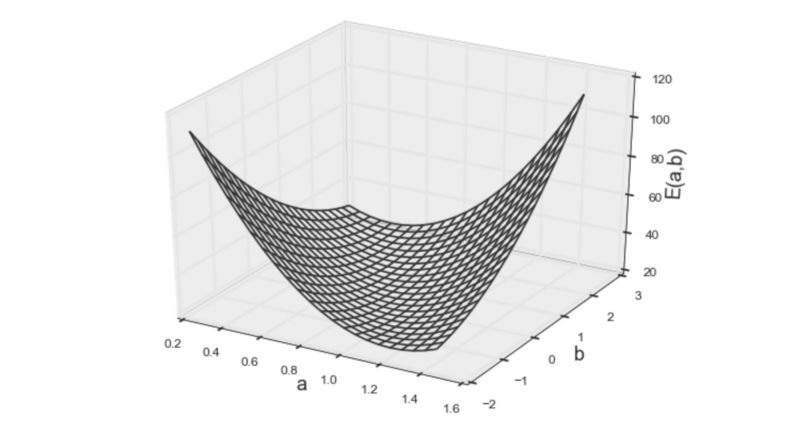图3 误差函数的第一个模型

 

从上方的3D图来看，人们会本能地猜测该函数为凸函数。凸函数的优化（找到最小值）比一般数学优化简单得多，因为任何局部最小值都是整个凸函数的最小值。（简单来讲，就是凸函数只有一个最小点，例如“U”的形状）由于凸函数的这种特性，通过简单求解如下的偏微分方程，便可得到使函数最小化的参数。

 

 

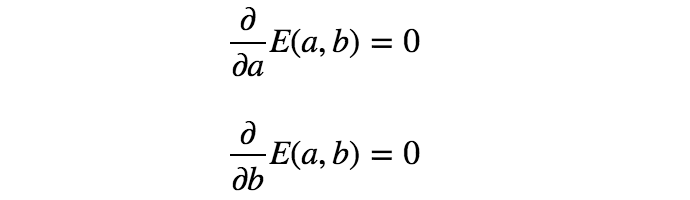
下面解下之前的例子吧。

 

 

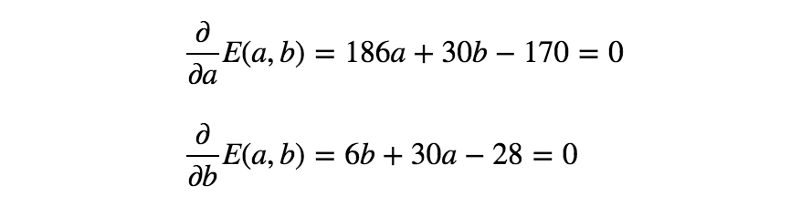
通过求解上面的等式，得到a = 5/6、b = 1/2。因此，第一个模型（最小化RSS）如下所示：

 

 

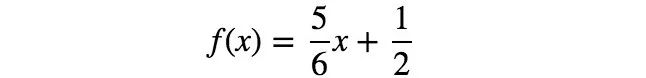
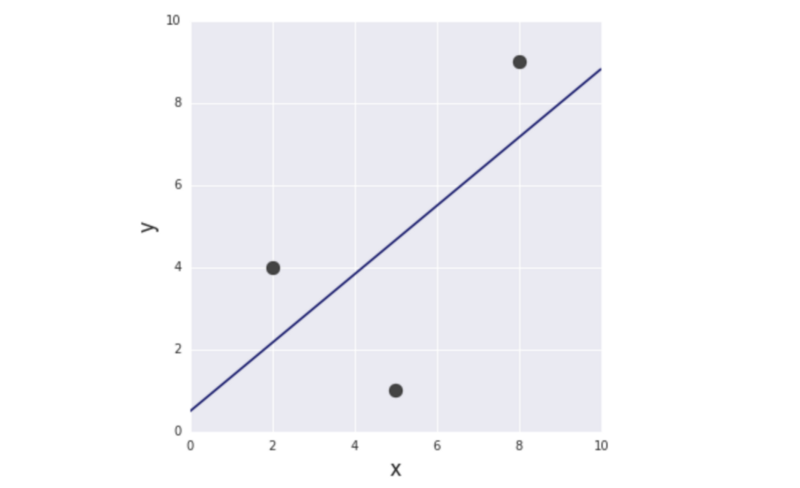
图4 第一个模型

 

示例2：简单的弯曲模型

 

现在，对于相同的数据点，可考虑如下的另一模型：

 

 

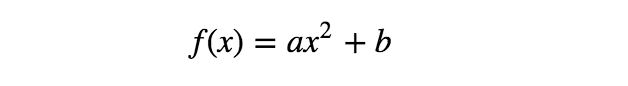
如上所示，该模型不再是输入变量x的线性函数，但仍是参数a、b的线性函数。

下面看下这一变化对模型拟合过程的影响。我们将使用与前一示例相同的误差函数——RSS。

 

 

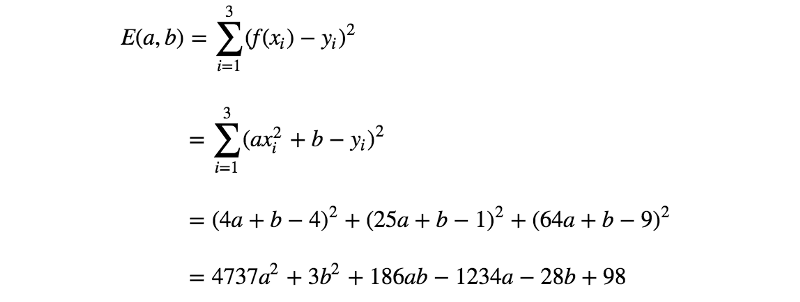
如上所示，等式看起来与前一个非常相似。（系数的值不同，但方程的形式相同。）该模型的可视化图像如下：

 

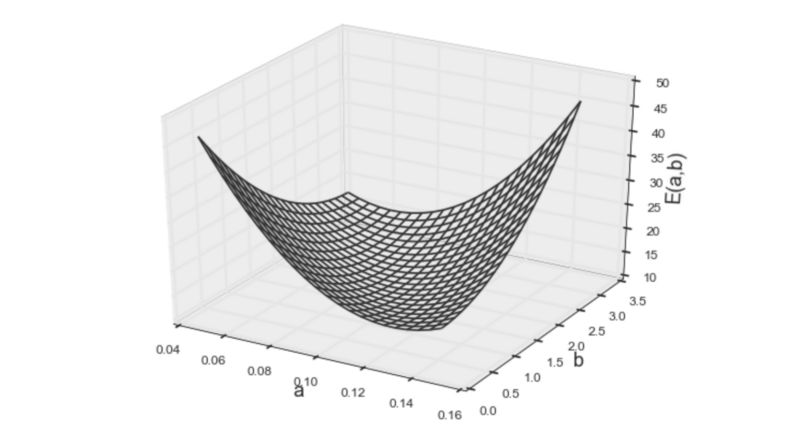
图5 误差函数的第二个模型

 

两个模型的形状看起来也很相似，仍然是凸函数。但秘密在于，当使用训练数据计算误差时，输入变量作为具体值给出（例如，x²的值在数据集中给定为22、52和8²，即（2,4）、（5,1）、（8,9））。因此，无论输入变量的形式多复杂（例如x、x²、sin（x）、log（x）等......），给定的值在误差函数中仅为常数。

 

误差函数的第二个模型也是凸函数，因此可通过与前一示例完全相同的过程找到最佳参数。

 

 

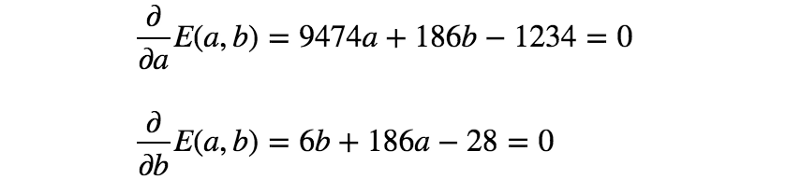
通过求解上面的等式，得到a = 61/618、b = 331/206。所以，第二个模型如下所示：

 

 

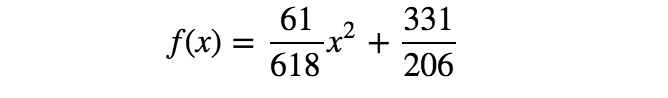
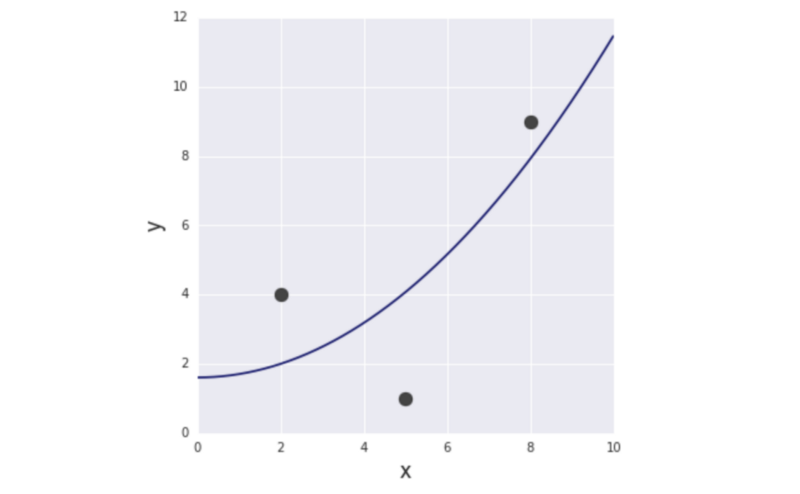
图6 第二个模型

 

结论：线性回归模型的线性假设

 

上述2个例子的求解过程完全相同（且非常简单），即使一个为输入变量x的线性函数，一个为x的非线性函数。两个模型的共同特征是两个函数都与参数a、b成线性关系。这是对线性回归模型的线性假设，也是线性回归模型数学单性的关键。

 

上面2个模型非常简单，但一般而言，模型与其参数的线性假设，可保证RSS始终为凸函数。通过求解简单偏微分方程，得到最优参数，这就是线性假设至关重要的原因。