本次Lecture主要介绍VC Dimension,从non-break point的角度来看之前break point对VC Bound的影响。最终得出结论要选择合适的来同时保证较小的
和较低的模型复杂度。

Recap
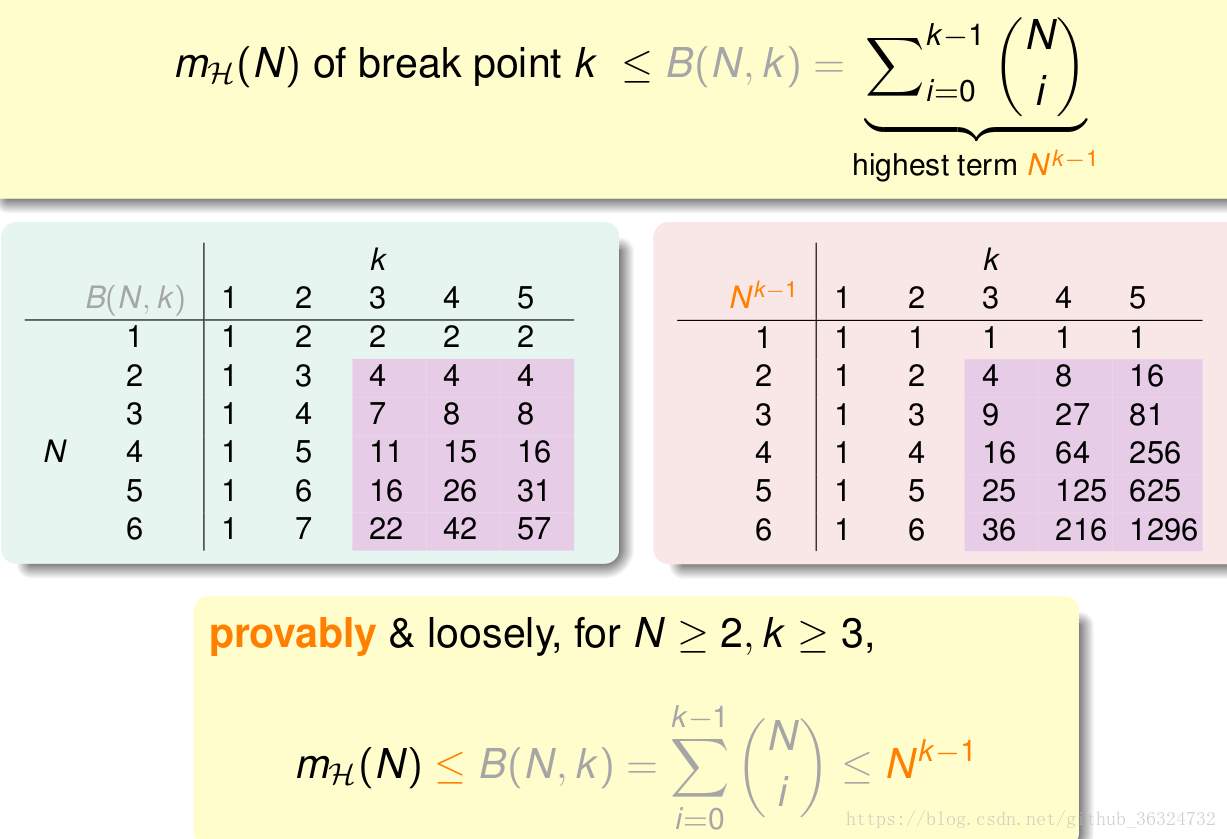
通过上节课的证明,我们知道了有多项式上界,这是在
的条件下的。我们又得到了VC Bound,这是在M无限的前提下的Hoeffding不等式,那么我们将
代入VC Bound,这样就只和N与k相关了。
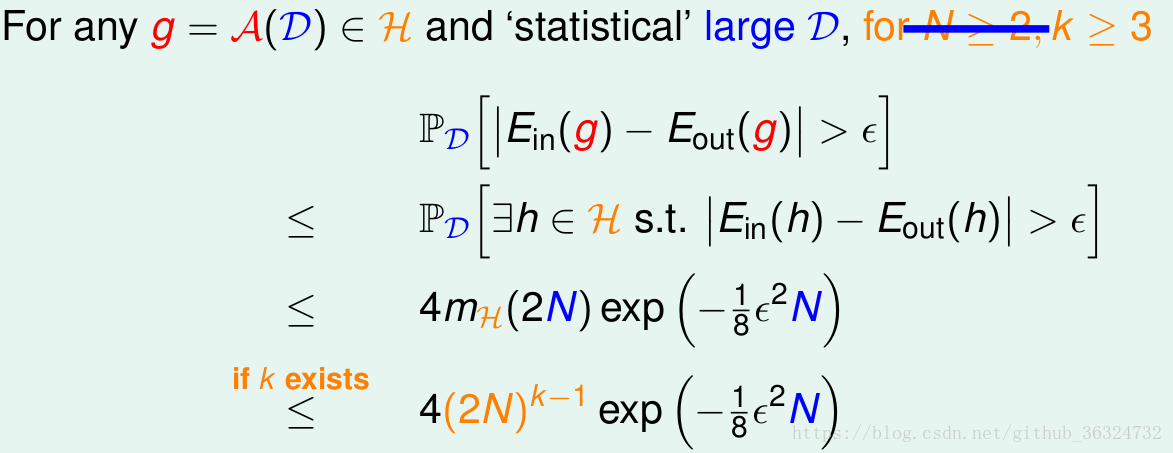
于是现在有几个条件——
有break point为k(好的H)
- N足够大
概率上可以有
(好的D)
- 算法能找出足够小的
(好的A)
能推断机器可以学习!
Definition of VC Dimension
引入定义VC Dimension为最大的non-break point点,也就是能shatter的input点数。根据之前对break point的定义(不能被shatter的最小点数),VC dimension的值。
此时就能用来替代k,得到以下结果——
![]()
从而就看到之前四个模型的VC Dimensions:
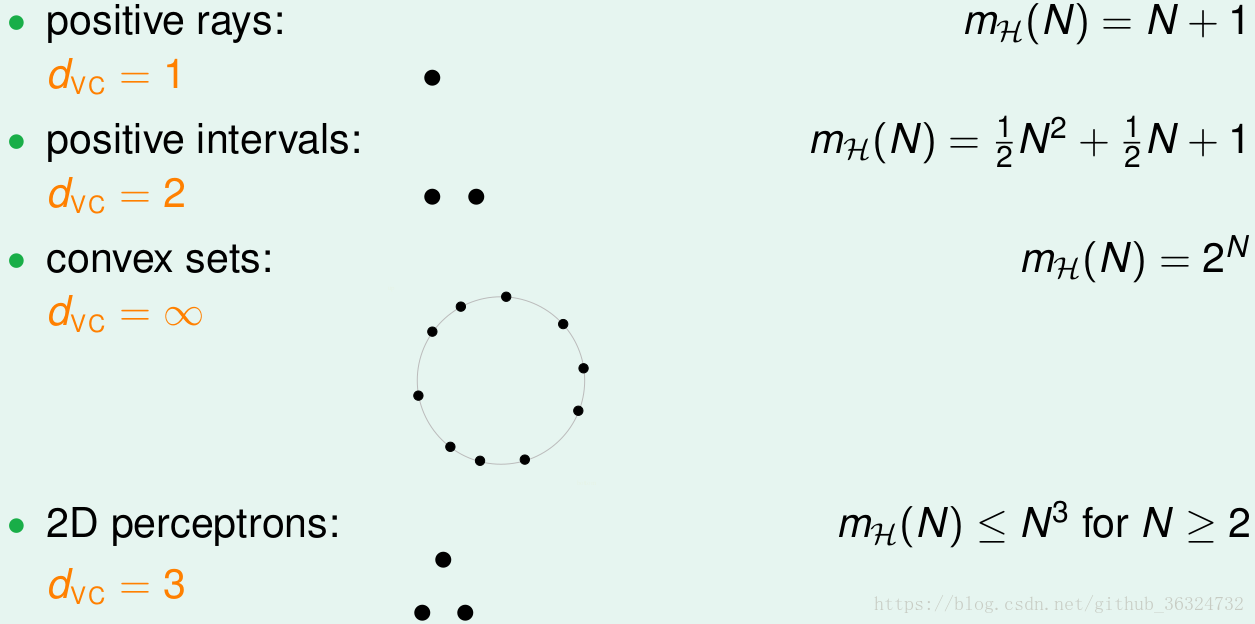
在这时,VC Bound的问题只和假设集H的和数据集D的
有关,与学习算法A、输入分布P、目标函数A都没有关系了。
VC Dimension of Perceptrons
回顾一下PLA,在2D Perceptrons的时候
- 假设训练数据集线性可分,PLA算法就可以收敛,经过T次(足够大)迭代后就能够得到一个g有
- 数据集服从某一未知的分布P,存在一未知的目标f,此时的
,那么当N足够大时,就有
以上两点融合就能证明机器学习可行。
那么如果在更多维的情况下呢?根据1D时和2D时
,猜测
。以下对此进行证明:
基本思路是,只要将两方面都证明即可。
,只要证明存在有d + 1的输入可以被shatter
构造一个d维的矩阵能够被shatter就行。
是d维的,原有d个inputs,每个inputs加上第零个维度的常数项1,得到
为d * (d + 1)的矩阵:
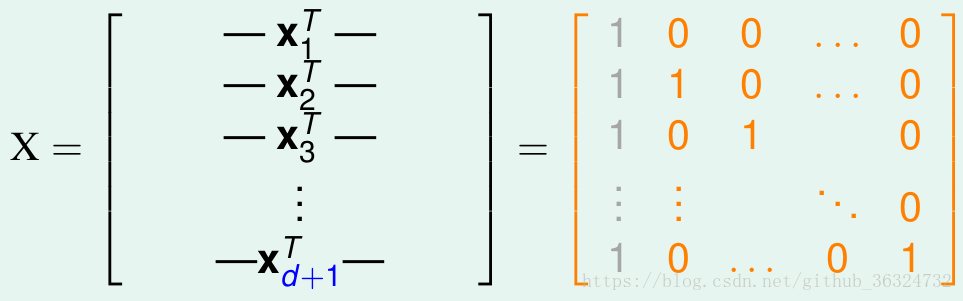
很显然,这个矩阵是可逆的。
shatter的本质是,H对中的每一行判断都是正确的,也就是对应着y。从而一定有
,由于
可逆,必有
。所以对于任意
都能找到一个
使得
。

由此证明第一个不等式正确。
,就要证明任意d + 2个输入都不能被shatter
任意d + 1维矩阵,包含d + 2个inputs,由于向量组所含向量个数多于向量的维数(d + 2 > d + 1),矩阵线性相关,某一列就可以用其他d + 1列线性表出,以
为例:
假设(蓝为+,红为-)
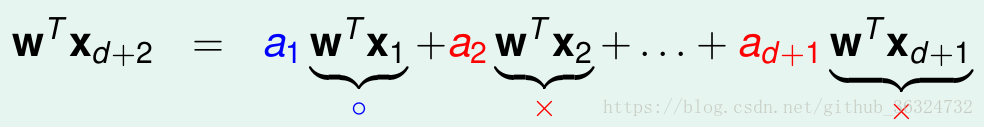 ,这个式子是 > 0的。
,这个式子是 > 0的。
在这种情况下,d + 2就被前d + 1项所限制而不能自由分类,当我们希望时,则产生矛盾。
由此证明第二个不等式正确。
- 综合以上两点,我们证明了
成立。
Physical Intuition of VC Dimension
这一节阐述VC Dimension的物理意义,它的实质是什么?

VC Dimension其实就是Hypothesis set的自由度,可以从三个方面来理解
- w中feature的个数,w是hypothesis的参数
- H中假设的个数M,这刻画了自由度的大小
- H的分类能力,就是最多能产生多少dichotomy
总之,就反映着假设集H的能力。

通常可以用自由参数的个数来看,但这不绝对,通常是个好方法。
过大或者过小的都会产生问题,选择合适的VC dimension很重要,所以选择模型是一件很重要的事。
Interpreting VC Dimension
之前的泛化不等式写到

这是在条件下,出现BAD的概率
,将其处理为表示GOOD的概率——
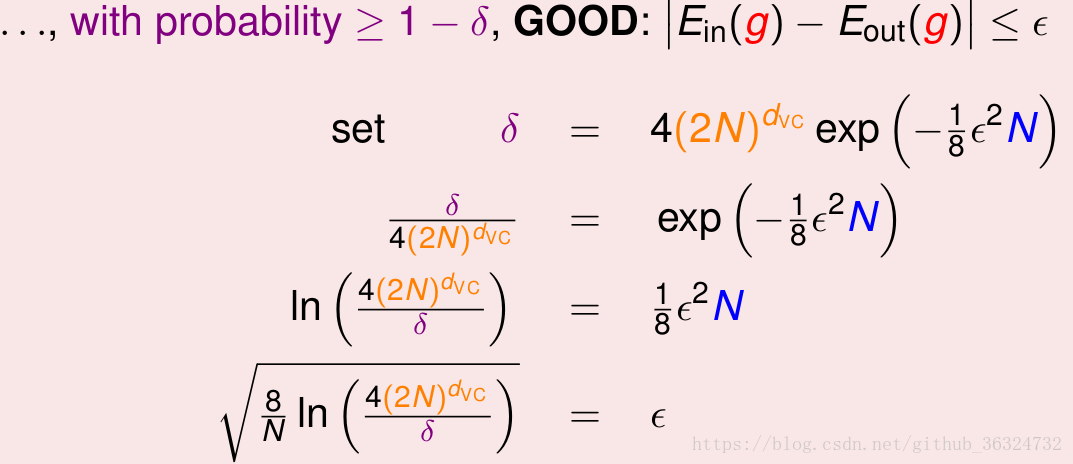
约束了假设空间H的泛化能力,
越小,泛化能力越大。

将根号用表示,不等式表示在一个很高的几率内,
的值会小于
。
至此,已经推导出泛化误差的边界,因为我们更关心其上界(可能的最大值),即:
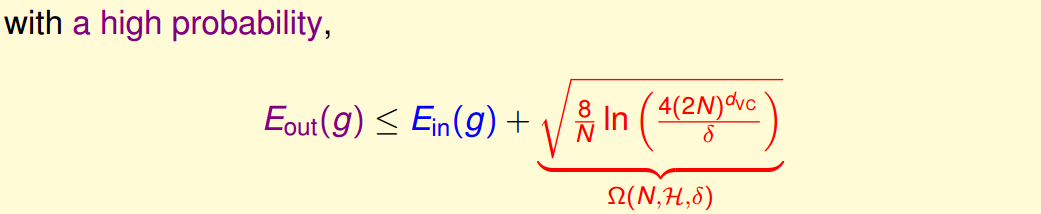
就表示了模型的复杂程度,它与数据集大小N、模型假设集
、错误容纳率
有关。下图表示了
、
、
与
的关系)——
 这说明H的选择要合适,选择出合适的
这说明H的选择要合适,选择出合适的能够得到更小的
。
下面的例子表明理论上的N大小,然而实际上就足够,这显示了VC Bound的宽松——

主要有以下四个原因——
- 使用了Hoeffding,让我们不用知道
;
- 使用成长函数
来计算任何数据的dicotomies个数上界;
- 使用
来替代
,这是上界的上界的上界;
- 在最差的情况下采用union bound,而算法并不一定会碰到极差的结果。
VC Bound对不同的model都有着差不多的宽松程度,可以利用这个横向比较来找出较好的model,宽松性对机器学习的影响就不是很大。
虽然之后大多不采用VC Bound的理论结果,但是我们还是要掌握其中的哲学信息。





 本文介绍了VC维度的概念及其在机器学习中的应用。通过定义VC维度为最大非断点数,并探讨了感知机的VC维度,解释了其物理含义。文章还讨论了如何选择合适的VC维度以确保模型具有良好的泛化能力。
本文介绍了VC维度的概念及其在机器学习中的应用。通过定义VC维度为最大非断点数,并探讨了感知机的VC维度,解释了其物理含义。文章还讨论了如何选择合适的VC维度以确保模型具有良好的泛化能力。
















 8702
8702

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








