这节课基于上节课与break point的关联,研究了
的上界
是否为多项式的问题,得到结论为多项式上界,并将其代入Hoeffding不等式,得到VC Bound,证明只要break point存在,机器学习就是可行的。

Restriction of Break Point
我们先看一下四个成长函数与break point的关系:

成长函数是一个hypothesis在N个数据点上可以产生的dichotomy数量的最大值。k为最小的break point,那么k + 1, k + 2...都是break point。
那么我们看一下当最小的break point限定为k = 2时能产生多少dichotomies?(也就是任意两个点都不能shatter,shatter的意思是对N个点,能够分解为种dichotomies)
- N = 1,从定义上显然
;
- N = 2,从定义上也有
;
- N = 3,我们可以从1开始尝试dicotomy的个数:1(ooo)、2(ooo、oox)、3(ooo、oox、oxo)、4(ooo、oox、oxo、xoo),若增加到5时必定会有两个点shatter,所以最大的
。
我们发现存在break point时会对最大值的大小产生限制,所以我们要尝试通过N与k来证明
是多项式级的,才能代入Hoeffding不等式,证明机器学习的可行性。
Bounding Function: Basic Cases
引入一个定义:上界函数(Bounding Function),表示了当break point = k时
可能的最大值。
从而我们只要对上界函数进行描述,就可以不考虑Hyphesis set的情况,不用因为问题的变化而有改变,这样就能简化我们的研究复杂程度。
我们可以通过下面这张表来尝试得到的分布情况——
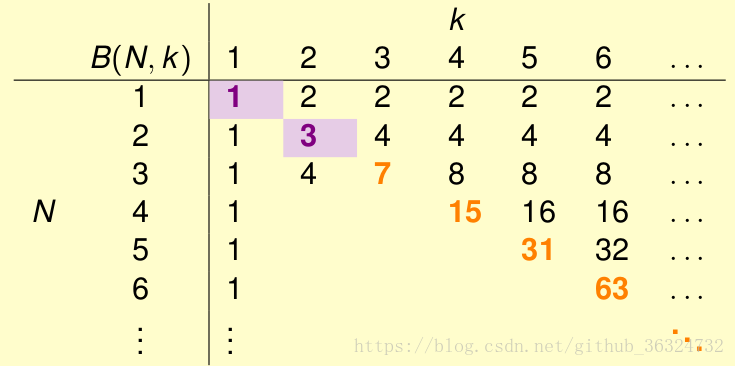
其中,根据之前的计算就能知道 和
;当k = 1时,任意的N取值都只会有一种“划线”方式,
(画画图就能看出来);
当
时,则所有的dichotomy都能满足条件,此时
;当N == k时,k = N是第一个不能shatter的值,所以去掉一个dichotomy就可以了,此时
。
其它更加常见的的求值比较复杂一些,相关的证明也留到下一小节。
Bounding Function: Inductive Cases
先以为例,寻找是否有递推关系。先把
可行的11条Dichotomies写下来并分组,如下——
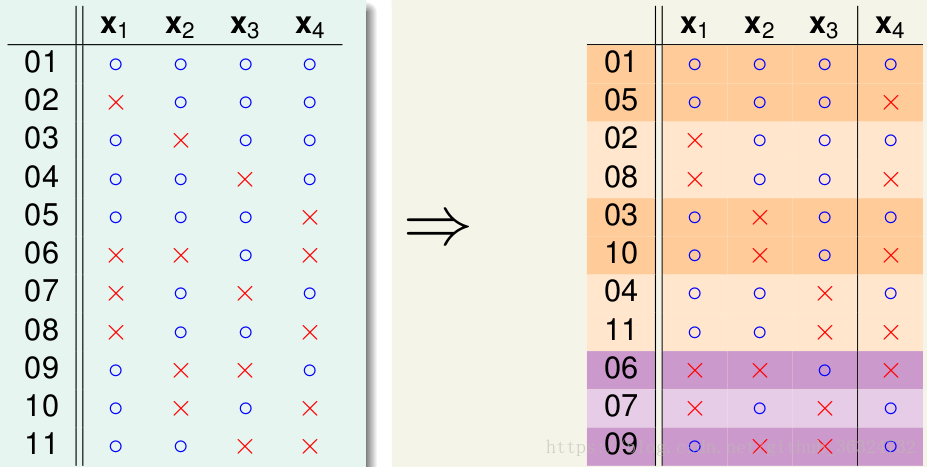
我们发现右图前8条是两两配对的,后3条是独立的,于是就有(
)。
- 根据定义,
中是不存在3个点shatter的,那么
中也是不存在3个点shatter的,于是
;
- 由于在
中是成对出现,且两两不同,于是必然有
中是
成对交错的,就可以将
划去,原先
任三个点不会shatter,在
中就有任意两个点不会shatter的结论,于是有
。
根据以上两点结论,我们可以将不等式左右相加,得到——
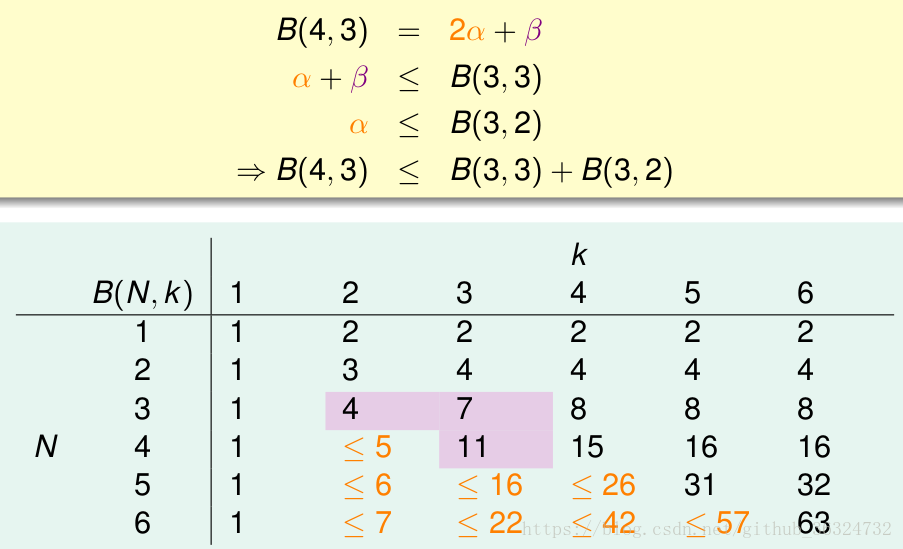
根据数学归纳法,就能够得到递推式结论:,得到通项式结论为
。
最大项也就是,证明了如果存在break point,
的上界就为多项式级的。
上式中 “” 可以通过数学严格证明为 “
” ,课程中不做要求。
A Pictorial Proof
现在我们知道了,有多项式级上界,如果能替代M代入Hoeffding不等式,就能得到
的结论。然而并不是直接代入就可以的,需要做一点变化,这样的原因是
是有限的,而
是无限的,实际的式子如下——
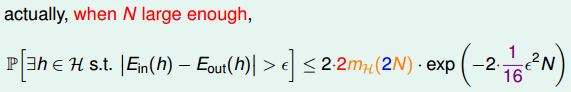
这个式子的证明比较复杂,数学推导不在课程中要求,主要分成以下三步——
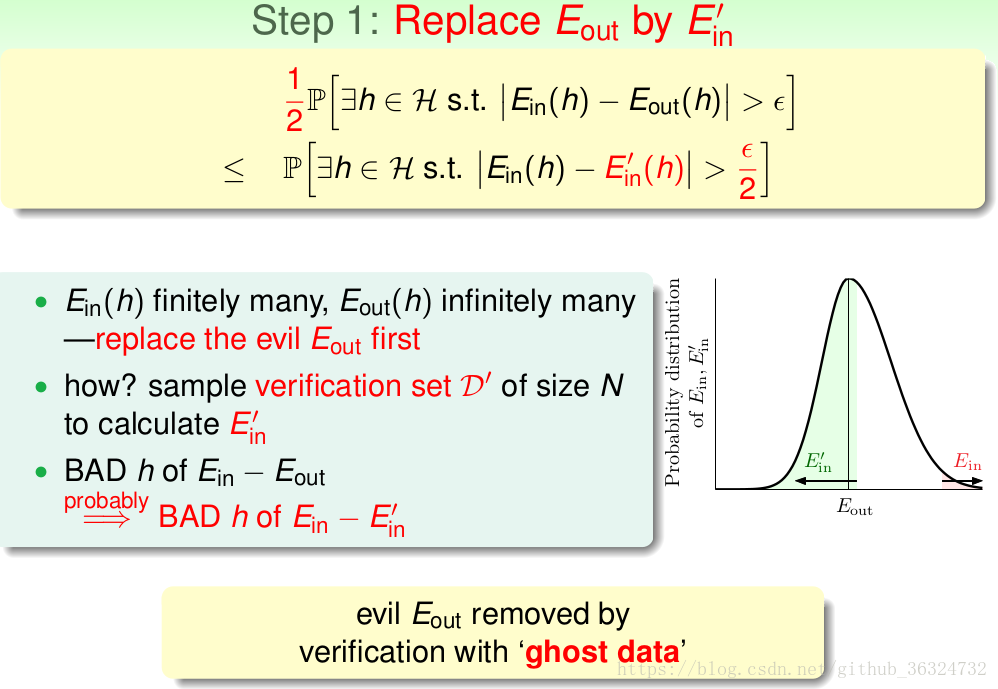
我们要将无限的用有限的
替换,也就是另外找一个大小为N的verification set来计算
。这里要将
变为
,满足数学上条件更严格的需要。
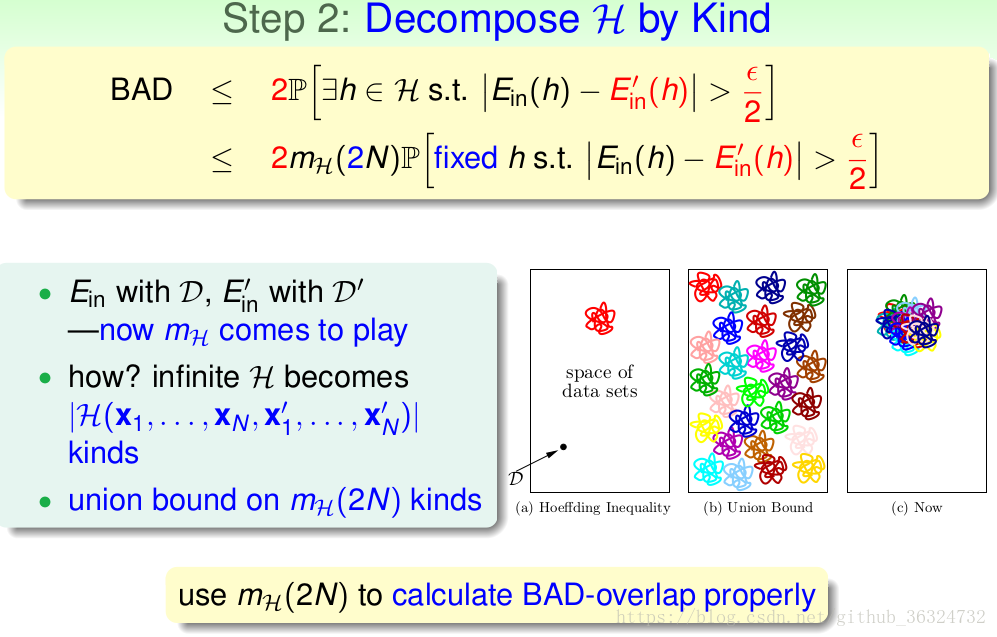
现在的Hypothesis set变为了,与之前同理,总共最多有
种hypothesis,然后再用union bound就能精确计算有多少BAD是重叠发生的。
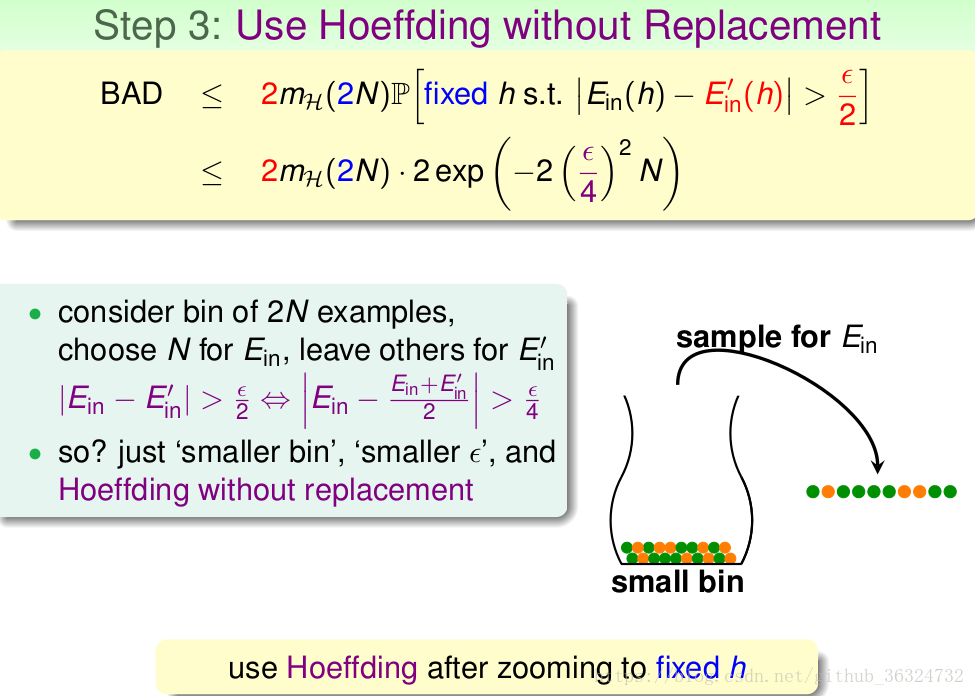
到现在我们有了一个固定的hypothesis set,可以想象有2N个点的罐子,从中抽取N个点作为,剩余N个点作为
,也就是用更小的罐子中采用更小的
做无放回抽样。这样就可以直接将式子代入Hoeffding's equality,得到结果。
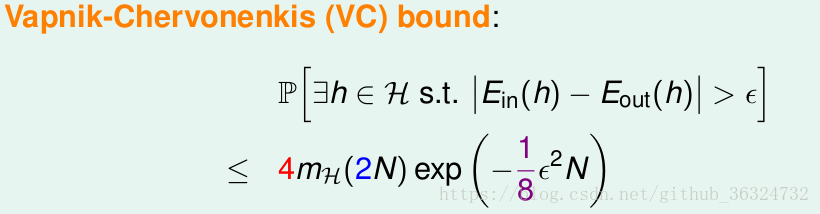
现在我们就得到了著名的VC Bound。
2D Perception的情况下,就有break point = 4,是
多项式上界的,从而证明2D Perception的学习是可行的。

这个题目说明了,VC Bound并不是一个很小的很准确的上界,那么为什么它这么有用?
下节课继续讲解。





 本文探讨了breakpoint的概念及其与成长函数的关系,通过数学归纳法证明了存在breakpoint时,成长函数的上界为多项式级别。进一步利用Hoeffding不等式推导出了VC-Bound,证实了机器学习的可行性。
本文探讨了breakpoint的概念及其与成长函数的关系,通过数学归纳法证明了存在breakpoint时,成长函数的上界为多项式级别。进一步利用Hoeffding不等式推导出了VC-Bound,证实了机器学习的可行性。
















 459
459

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








