台大机器学习基石 Lecture 5 - Training versus Testing_machine learning foundations lecture 5 training ve-优快云博客

本文回顾了机器学习的基本原理，提出了两个核心问题：如何确保经验风险逼近真实风险，以及如何减小经验风险。讨论了在无限假设集上的学习可行性，通过引入有效假设数的概念，将无限假设集转化成有限类别进行分析。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

本次Lecture先将之前一部分对“When Can Machines Learn”中的内容梳理了一下，归结为机器学习的两个核心问题： $E_{in}(g)\approx E_{out}(g)$ ？ $E_{in}(g)\approx 0$ ？然后研究在无限hyphothesis set上如何归类，成为一个在有限的M上（也就是 $m_H(N)$ ）的问题，并且试图求出 $m_H(N)$ ，并探讨其什么时候是非指数形式，这样机器学习才有效。

Recap and Preview

我们在之前的课程中得出的结论：只要数据集足够大，hyphothesis有限个，就能证明每个hyphothesis的 $E_{in}(h) \approx E_{out}(h)$ ，从中就能让机器学习算法选出一个最低的 $E_{in}(h)$ 使之成为 $g$ ，根据PAC就能知道 $E_{in}(g)\approx E_{out}(g) \approx 0$ ，从而机器学习是可行的。

$B_i$

通过上图就能把前4次Lecture的内容串起来，机器学习就分成了两个核心问题——

我们能否保证 $E_{in}(g)$ 与 $E_{out}(g)$ 是足够接近的？
我们能否让 $E_{in}(g)$ 足够小？

那么，对于有限的M来看，当M较小时，坏事情发生的几率很小，但g的选择范围又太小；当M较大时，g的选择范围够大，但坏事情发生的几率又增大了。因此，就算当M是无限大的时候，我们也要选择一个合适的（不太大又不太小）有限的 $m_H$ 来替代M，然后我们要证明在无限M的前提下学习的可行性，以及如何选择“正确的”hyphothesis set H。

Effective Number of Lines

在推导M个hypothesis的Hoeffding不等式时，我们用到了级联（union bound）：

$\mathbb{P}\left [ B_1 or B_2or...B_M \right ]\leq \mathbb{P}\left [ B_1 \right ]+\mathbb{P}\left [ B_2 \right ]+...+\mathbb{P}\left [ B_M \right ]$

这是基于 $B_i$ 互相之间是独立的，而他们实际上有交集有重叠的，这位就导致级联over-estimating了。

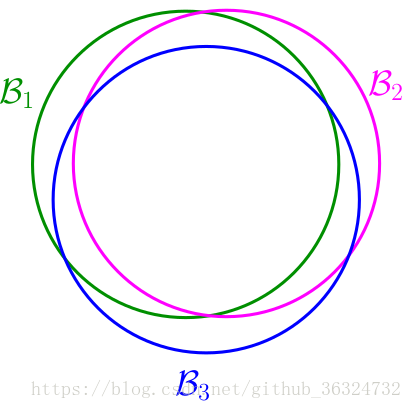
从而我们知道M没有那么大，我们能不能找出重叠部分，将无限的hypothesis set转化为有限个类？

我们看到将data分为相同的+1和-1方法的hypothesis是相似的，这些可以被归为1类。

在2D的平面上，hypothesis就是一条直线，那么点的个数和划分方法数对应如下——

点的个数N	划分方法数effective(N)	图例
1	2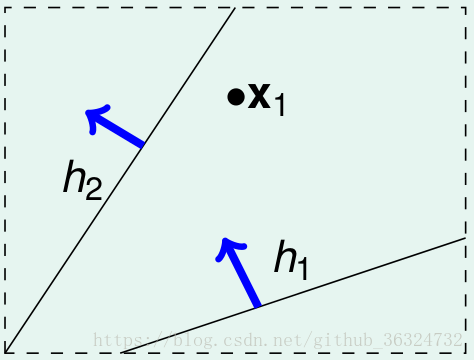
2	4
3	6或8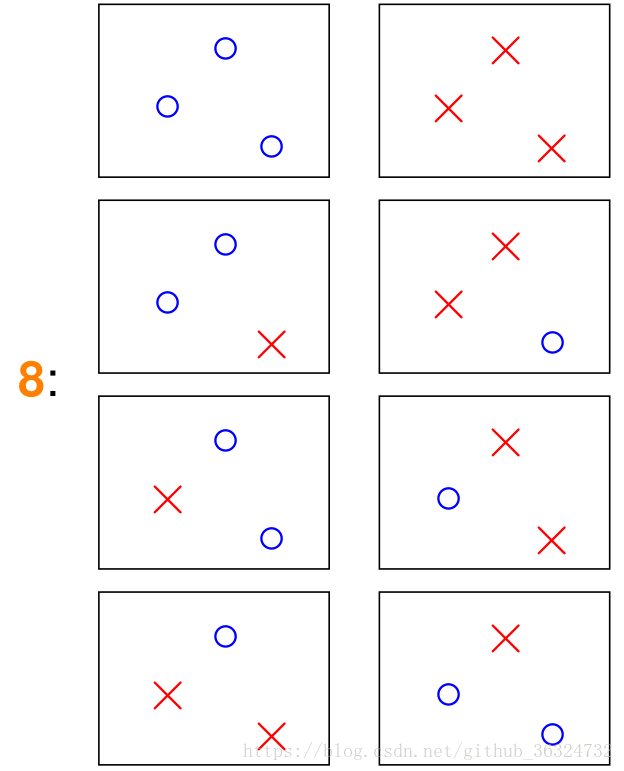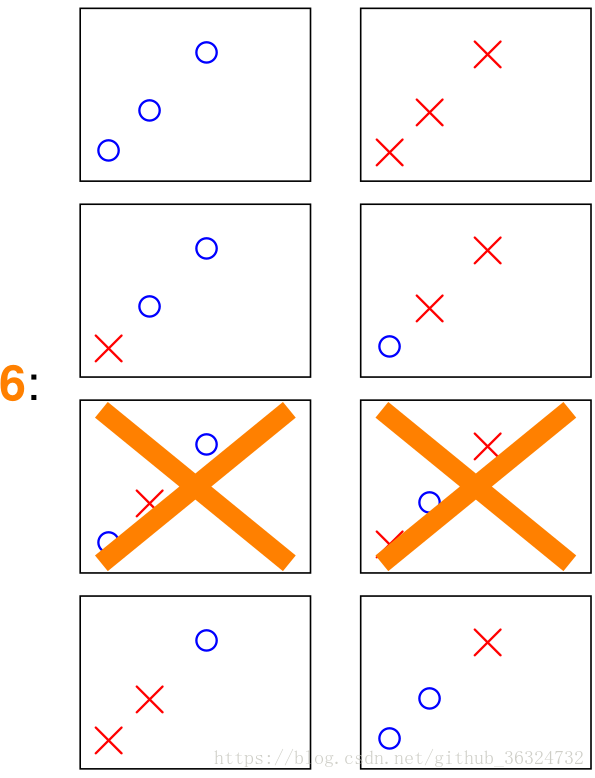
4	$\leq 14$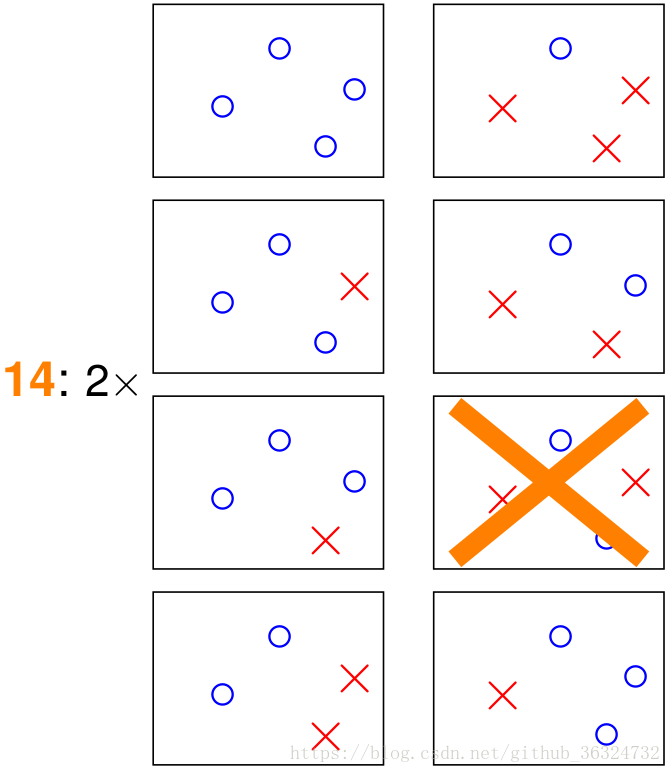

显然我们看到在N个输入点的情况下，也每一个点都有两个状态二选一，有效直线的个数 $\leq 2^N$ 。从而我们看到M显然是有上界为effective(N)，那么Hoeffding不等式就能被改写为——

$\mathbb{P}[\left | E_{in}(g)-E_{out}(g) \right | > \varepsilon ]\leq 2\cdot effective(N)\cdot exp(-2\varepsilon ^2N)$

已知 $effective(N)\leq 2^N$ ，如果有 $effective(N)\ll 2^N$ 就能保证在无限多的hypothesis上的机器学习可行。

Effective Number of Hypothesis

引入一个新的概念dichotomy，就是将空间中的点（例如二维平面）分成正类（蓝色o）和负类（红色x）。

用这种方式来表示每一种hypothesis，数学表达如： $H=\{ hypothesis\ h: \chi \rightarrow \{ \times ,\circ \} \}$

定义 $h(x_1,x_2,...,x_N) = (h(x_1),h(x_2),...,h(x_N)) \in \{\times, \circ\}^N$ 来表示一个hypothesis对数据集的分类情况，每个h都是由 $x_i$ 的情况来表达。对假设集 $H$ 和 $H(x_1, x_2, ... , x_N)$ 有如下区别——

我们定义成长函数(Growth Function)： $m_H(N) = \max \left | H(x_1,x_2,...,x_N) \right |$ ，通过所有 $(x_1,x_2,...,x_N)$ 所产生的 $\left | H \right |$ 中的最小值来消除对数据的依赖。其实这个成长函数就是之前 $effective(N)$ 的最大值。

然后的问题是怎么求成长函数 $m_H(N)$ 呢？

课程中给出了三种具体情况的求解：

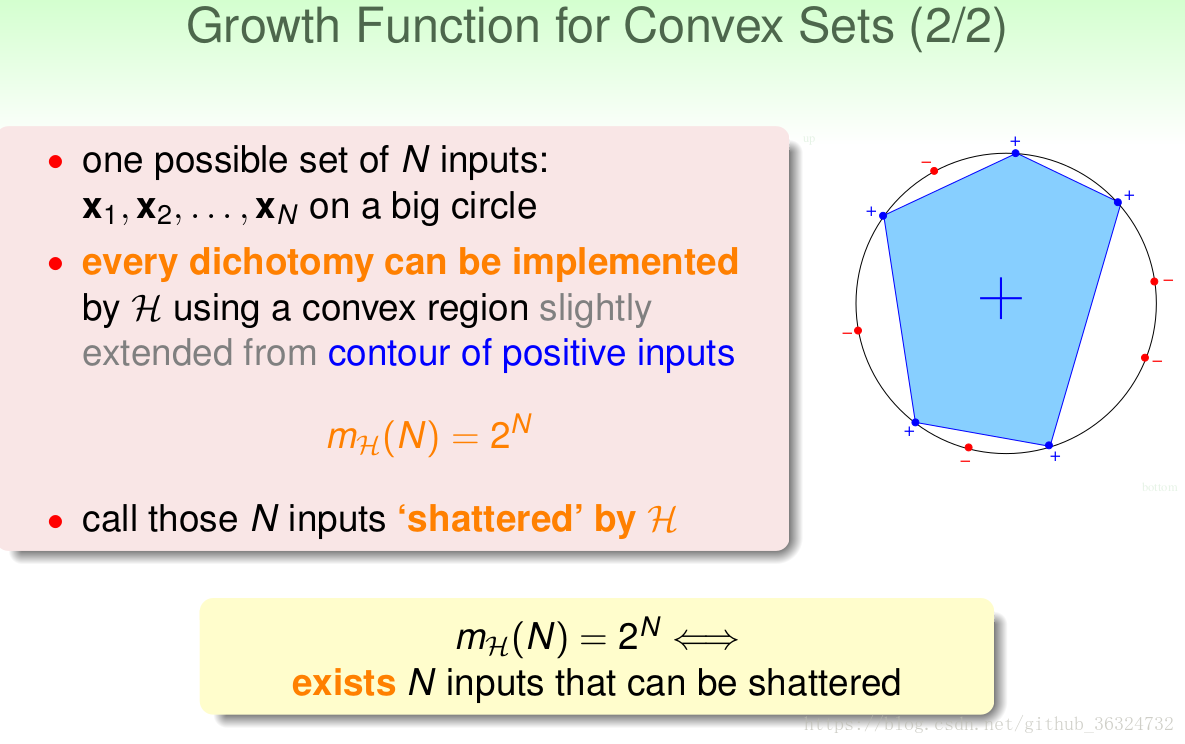
也就是在平面上任意多个点，只要能被shatter掉（这个词不知道怎么解释比较好？分散开？），就有 $m_H(N)=2^N$ 。

总结以下就是——

Type	$m_H(N)$
positive rays	$N+1$
positive intervals	$\frac{1}{2}N^2+\frac{1}{2}N+1$
convex sets	$2^N$

Break Point

从上面我们能看到前两个的 $m_H(N)$ 是多项式级的，而第三个是指数级的。而我们希望 $m_H(N)$ 是多项式级的，这样在N增长的时候 $m_H(N)$ 增长较慢， $E_{in}(g)$ 和 $E_{out}(g)$ 相差很大的几率才能越来越小，这样机器学习才是可行的。

对于2D Perception模型，我们之前证明了N = 3时能shatter，而N = 4时则完全不能，此时就成k = 4为H上的break point，那么k > 4的时候也为break point（显然可以先去掉一些点不满足，加上点后仍然不满足），因而我们只要研究最小的break point就可以了。

以上我们发现，当没有break point时（比如convex sets）， $m_H(N) = 2^N$ ；当存在break point为k时，是否有 $m_H(N) = O(2^{k - 1})$ 呢？这一点在positive rays、positive intervals、2D perception模型中都适用，我们对此猜测的证明将在下一节课完成～如果证明成功，我们就能够将 $m_H(N)$ 代替M，从而机器学习就可行了。