【手撕机器学习经典算法-01】KNN（K-邻近）算法

本文链接：https://blog.youkuaiyun.com/gitTung/article/details/146324480

前言

最近在上一门《机器学习算法实验》的课程，有一些课堂小实验，还要写实验报告，笔者已经两三年没有写过实验报告了，梦回本科了属于是。刚好借此机会，开启一个“手撕机器学习十大经典算法”的系列，通过动手实践，掌握算法的原理。今天要分享的是KNN（K-邻近）算法。

问题描述

编写实现KNN分类器，利用钞票鉴别数据集测试KNN分类器效果，并对比sklearn工具包的分类结果。

基本原理

K-近邻算法采取多数表决，无需求解计算模型参数，也无需训练过程。只需要提供一组带标签的训练数据，因此属于监督学习算法。

算法原理：给定一组训练数据（包括特征和标签）和一个参数k，计算输入特征向量到训练数据各样本的特征向量的距离，选取距离最近的k个样本，根据这k个样本中的标签数进行投票表决，票数最多的标签即为预测结果。

KNN算法三要素：

k的取值：应当适中
距离度量：欧式距离、马氏距离等
分类决策：多数表决投票决策

KNN算法描述

给定n个训练样本(x_i, y_i)，i=1,…,n，其中x_i为样本i的特征向量，y_i为标签值，设定参数k。待分类样本的特征向量为x，则KNN算法预测其标签的算法步骤如下：

迭代所有训练样本
对于每个样本i，计算特征向量x_i与x之间的距离d_i
从n个样本中选取d最小的k个样本，作为邻近样本
统计k个邻近样本中每个标签出现的次数
选择出现频率最高的标签作为待分类样本的预测结果类别

代码详解

需要提前安装的包有：

numpy
pandas
sklearn：
matplotlib：用来绘图
tqdm：可选，用来展示模型训练/预测进度

step1：引入需要使用的包

import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
import matplotlib.pyplot as plt
from tqdm import tqdm

step2：定义一个class，封装KNN模型的拟合和预测方法

class KNN(object):
    def __init__(self, k):
        self.k = k
        self.X_train = None
        self.y_train = None

    def fit(self, X_train, y_train):
        self.X_train = np.array(X_train)
        self.y_train = np.array(y_train)

    def predict(self, X_test):
        X_test = np.array(X_test)
        X_train_len = len(self.X_train)
        x_test_len = len(X_test)
        pred_label = []		# 用来存储每个待测样本的预测结果标签

        for test_len in range(x_test_len):		# 遍历所有待测样本
            dis = []							# 用来存储所有训练样本到当前待测样本的距离
            for train_len in range(X_train_len):# 遍历所有的训练样本
                dis.append(np.sqrt(np.sum((self.X_train[train_len] - X_test[test_len]) ** 2)))	# 计算欧式距离
            dis = np.array(dis)					# 转为np.array是为了使用numpy的argsort方法
            index = np.argsort(dis)				# argsort方法计算排序后的元素在原数组中的下标值
            label = []							# 用来记录k个最邻近样本的标签
            for i in range(self.k):				
                label.append(self.y_train[index[i]])
            pred_label.append(max(set(label), key=label.count))	# 将label中出现次数最多的元素作为分类结果加入到pred_label中
        return pred_label

k值作为非常重要的参数，我们在模型创建时就初始化
因为KNN算法完全不需要训练，所以实际上fit函数，只是保存下了训练样本（或者可以理解成训练样本就是模型参数）
predict函数，对一组测试样本进行分类，详细解释参考代码注释。
这里稍微解释一下pred_label.append(max(set(label), key=label.count))这行代码
max函数有两个参数：
- set(label)：将label转化为集合，以去重
- label.count：是一个函数，接受一个参数，返回label中该值出现的次数
将label.count作为max函数的key参数，则在对 set(label)求最大值的过程中，会基于该值出现的次数来排序

step3：声明一些工具方法

# 声明一个计算准确率的方法
def get_accracy(y_true, y_pred):
    accracy = 0
    for i in range(len(y_true)):
        if y_true[i] == y_pred[i]:
            accracy += 1
    return accracy / len(y_true)

# 使用指定的模型和数据，预测和计算准确率
def pred_and_accracy(model, X_train, X_test, y_train, y_test):
    model.fit(X_train, y_train)
    pred = model.predict(X_test)
    return pred, get_accracy(y_test, pred)

step4：编写主函数

本代码使用的银行钞票鉴别数据集，可点击进入网站下载
该数据集一共5列，前4列为特征，最后一列为类别（真/伪）

def main():
    # 输入数据和预处理
    filename = 'data_banknote_authentication.txt'
    col_name = ['variance', 'skewness', 'curtosis', 'entropy', 'class']
    dataset = pd.read_csv(filename, header=None, names=col_name)
    data = dataset.values
    feat = data[:,:-1]
    label = data[:,-1]
    # 划分训练集和验证集
    X_train, X_test, y_train, y_test = train_test_split(feat, label, test_size=0.2, random_state=100)
    print(X_train.shape, X_test.shape, y_train.shape, y_test.shape)
    
    my_accs = []    # 记录我的KNN模型的准确率
    sk_accs = []    # 记录sklearn库提供的KNN模型的准确率

    # 遍历不同的k，分别计算两个模型的准确率
    k_range = range(1, 50)
    for k in tqdm(k_range):		# 使用tqdm可以在控制台中展示当前的迭代进度
        # 我的KNN模型
        my_knn = KNN(k)
        pred, acc = pred_and_accracy(my_knn, X_train, X_test, y_train, y_test)
        my_accs.append(acc)
        # sklearn库提供的KNN模型
        sklearn_knn = KNeighborsClassifier(n_neighbors=k)
        pred, acc = pred_and_accracy(sklearn_knn, X_train, X_test, y_train, y_test)
        sk_accs.append(acc)
    
    # 使用折线图绘制准确率随k取值的变化曲线
    fig = plt.figure()
    ax = fig.add_subplot(121)
    ax.set_title('My KNN')
    ax.set_xlabel('k')
    ax.set_ylabel('Accuracy')
    plt.plot(k_range, my_accs)
    ax = fig.add_subplot(122)
    ax.set_title('sklearn KNN')
    ax.set_xlabel('k')
    plt.plot(k_range, sk_accs)
    plt.show()


if __name__ == '__main__':
    main()

案例测试结果

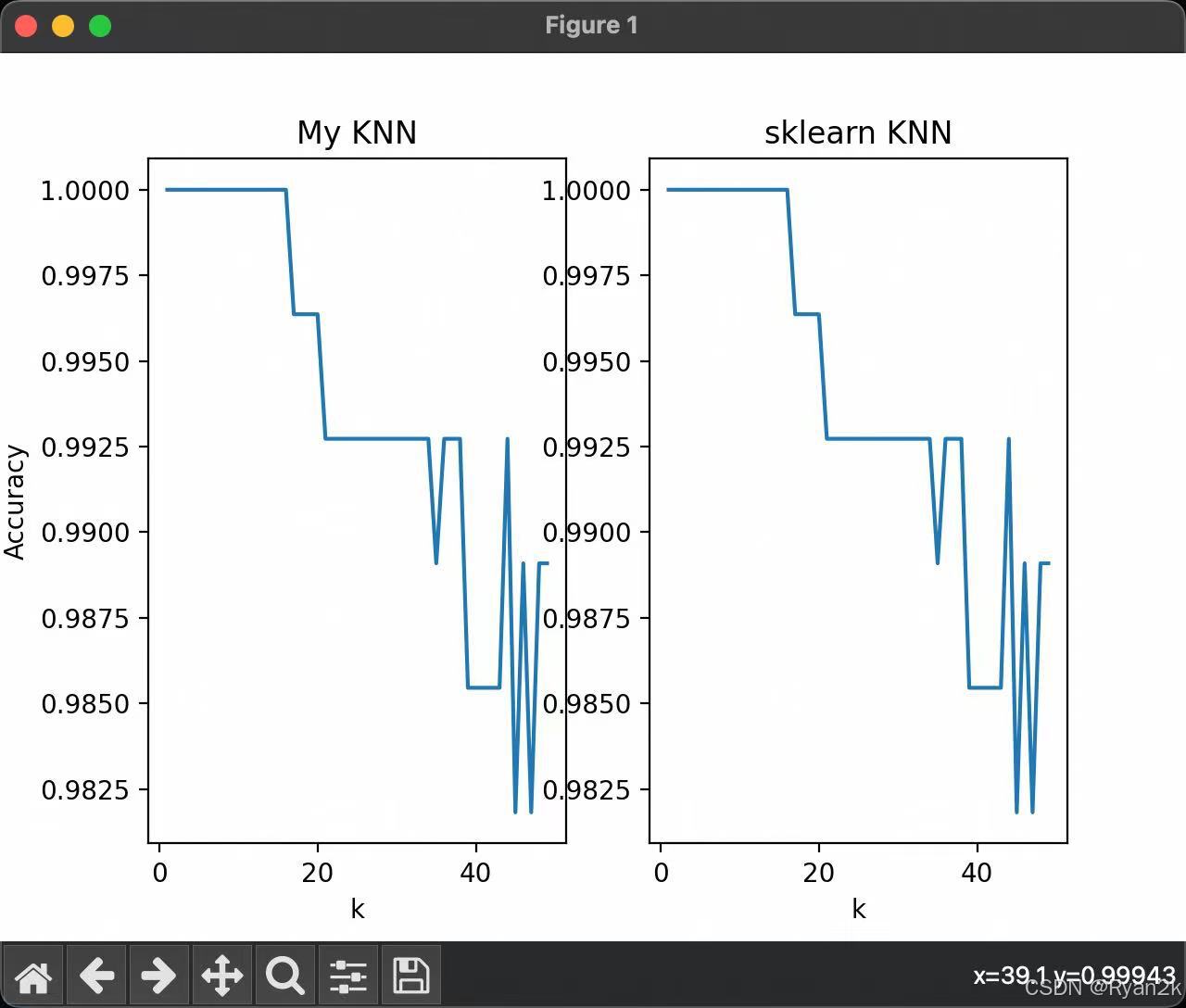
在这里插入图片描述
当k的取值大于一定值后，算法的准确率开始下降和波动。

一些思考和问题

时间复杂度优化

如果分析一下本代码中的时间复杂度，可以发现，由于进行了全排序，假设采用快速排序，时间复杂度为O(nlogn)。但实际上不需要进行全排序，只需要排出前k个样本即可。那么可以考虑插入排序或者选择排序，那么时间复杂度为O(kn)，通常k<<n。如果再极端一点，可以用堆排序，建堆的时间复杂度为O(n)，排k个最小值的时间复杂度为O(klogn)。
本代码中使用欧式距离作为距离度量，不同距离度量之间有什么区别？如何选择？
这个问题笔者懒得研究了，先贴出chatgpt的回答，后续有需要时可作为参考：