基于LSTM的钢琴MIDI双轨分离

单轨到双轨钢琴MIDI文件的LSTM模型

摘要

通过MIDI保存的钢琴乐谱便于机器演奏，但当普通人想要使用这种乐谱演奏音乐时，会发现难以区分左右手乐谱。本文提出了一种基于结合了长短时记忆（LSTM）和“Map”的神经网络的算法。通过使用该算法，可以将MIDI文件中的单轨钢琴乐谱分割为双手钢琴乐谱。

索引术语

信号处理，神经网络，长短期记忆，人工智能，钢琴谱

一、引言

乐谱通常被认为是音乐家用来象征歌曲演奏的作品。
除了人类熟悉的乐谱记号外，MIDI文件格式中还包含大量音符。MIDI是乐器数字接口（Musical Instrument Digital Interface）的缩写，通常通过音乐自动转录从传统乐谱或键盘录音转换而来。理想情况下，MIDI应包含乐谱的所有必要信息。然而，人们获得的MIDI文件由一系列音符组成。这对机器来说不是大问题，但对于人类演奏者而言，有必要将乐谱进行分轨以便于演奏。

在本文中，我们重点关注对算法至关重要的两种键盘状态。一种称为“热状态”（HOT state），即当前时间步将要按下的键。使用热状态作为算法的表示形式被称为热图（HOT‐map）。另一种定义为“开启状态”（ON state），表示在此时间步之前已经被按下的键。与热图类似，使用开启状态作为算法的表示形式被称为开启映射（ON‐map）。
弄清这两种图有助于更好地处理MIDI数据。

二、相关工作

钢琴手部分配是将合并的音乐轨道分离为双轨乐谱。
通常，声部分离的任务是将复调音乐划分为单声部，其中包含遵循传统和声进行规则的单声部音符序列。
如果我们将混合钢琴乐谱（单轨）视为一段复调音乐，那么将合并的乐谱轨道分离为双声部的任务就相当于声部分离。格雷和布内斯库 [1] 应用了一个隐层神经网络进行声部分离。但对于手部分配任务而言，和弦存在于一个轨道中，打破了传统规则。此外，该结果声部分离的结果可能包含多个声部或序列，但普通钢琴谱只有两个音轨。因此，通过声部分离提取出的单声部应被适当地合并为双声部。在[2]中，作者提出了一种允许单个声部中包含和弦的方法。这样，他们的方法也可以应用于钢琴手部分配任务。

在传统规则中，声部内不存在重叠的音符，但对于手部分配任务而言，音轨中的和弦打破了这些传统规则。在[3]中，作者提出了一种允许单一声部中存在和弦的方法。通过这种方式，他们的方法也可以应用于钢琴手部分配任务。
我们所处理的音符手部分配问题是一个典型的序列标注问题[4]。序列标注被定义为给序列中的每个位置分配一个标签的任务。在我们的案例中，需要为乐谱中的每个音符分配一个左右手标签。传统的算法如马尔可夫模型 [5]或条件随机场模型[6]被用于处理此类数据。随着深度神经网络研究的最新进展，长短期记忆网络在各种序列标注任务中越来越受欢迎。其中关键的是双向长短期记忆网络[7]，它使模型能够访问序列中的过去和未来信息。
例如，Kwon, Jeong, Nam[8]将双向长短期记忆网络应用于自动音乐记谱，解决了音频到乐谱对齐的问题，同时将一段钢琴录音转换为乐谱。

III. 实验

乐谱的划分应基于双手音符数量几乎相等的原则。在键值50到90之间，两种分布有显著重叠，这符合常识。
我们可以大致通过键值60（中央C键）将乐谱中的大部分音符分到左轨和右轨，但其准确率并不令人满意。因此，我们提出一种基于LSTM模型的音符分割算法，并尝试了若干变体，以获得最适用的算法。

A. 网络结构

在这项研究中，我们使用循环神经网络模型[9]。也就是说，我们将一系列重新打包的音符作为输入提供给模型，模型则输出每个音符的手部分配。这是一个典型的序列标注问题[4]。一个标准的循环神经网络模型可以如方程（1）所述，其中 $x_t$ 是当前时间步的序列输入向量；$h_t$ 是隐藏层向量；$f_h$、$f_y$ 是激活函数；$W$、$U$、$b$ 是参数矩阵和向量。

$$
h_t = f_h(W_h \cdot x_t + U_h \cdot h_{t-1} + b_h) \
y_t = f_y(W_y \cdot h_t + b_y)
\tag{1}
$$

在循环神经网络（RNNs）中，利用当前输入和前一隐藏状态来计算当前输出以及新隐藏状态。这种循环结构使RNN能够记忆过去状态。然而，由于梯度消失问题，RNN通常只能在短时间窗口内有效记忆信息。因此，常采用长短时记忆网络（LSTM）这一循环神经网络模型的变体来克服此类问题。
对于手部分配预测，对模型输出进行简单的四舍五入操作将得到一个由“0”和“1”组成的数组。其中，“0”表示左手分配的预测或填充元素，而“1”表示右手分配。
由此，我们得到了手部分配预测。基于这些预测，可以计算模型预测的错误率，如公式(2)所示，其中ER是错误率的缩写，$I(x)$ 是指示函数，$\lfloor x \rfloor$ 是最接近整数函数，$\sigma$ 是Sigmoid函数，$y$ 是目标标签，$\hat{y}$ 是模型预测，$M$ 是掩码‐映射，$T$ 是乐谱块的长度，$L$ 是键编码列的宽度，在本研究中该宽度为10。

$$
ER = 1 - \frac{1}{\sum_{t=1}^{T}\sum_{l=1}^{L} M_{tl}} \cdot \sum_{t=1}^{T}\sum_{l=1}^{L} I(\lfloor \sigma(\hat{y} {tl}) \rceil \neq y {tl}) \cdot M_{tl}
\tag{2}
$$

第四节 乐谱分离算法

A. 算法A：基于热图表示的手部分配

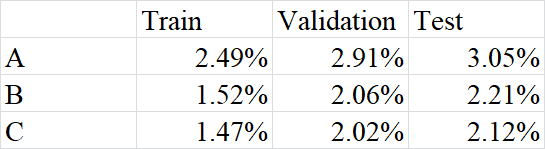
对于MIDI文件，我们从选定的MIDI文件中提取HOT图、标签图和掩码图，并通过上述方法将这些图分割成256大小的小块。模型优化过程通过标准Adam优化器[10]和默认超参数设置完成。在每一轮训练轮次中，使用验证集对训练好的模型进行评估，如果验证准确率有所提升，则保存该模型。训练完成后，选取验证准确率最高的模型，在测试数据集和独立测试集上进行评估。该实验结果如图1所示。该模型的错误率低于约15%的中央C基线。

B. 算法B：基于HOT图和时长图表示的手部分配

在算法A中，我们仅考虑音高而不考虑按键的持续时间。这种方法忽略了一个重要因素，即如果有多个手指已经按下了琴键，则后续的指法会受到影响。因此，我们需要从MIDI中提取时间信息，也就是每个HOT键的持续时间。以这些新的序列作为输入，结果如图1所示。超参数用于神经网络训练的设置与算法A实验所用的设置相同。
在测试集上评估的错误率为2.21%，低于算法A。

C. 算法C：基于热图和ON-映射表示的手部分配

可以发现，算法B只是对算法A进行了轻微修改。时间属性被直接添加到输入数据中，但这种信息可能难以让模型学习。因此，在算法C中，我们构建了另一种将时间信息注入输入数据的方法。当我们在键盘上演奏一个音符时，按下键的集合会对手的位置和移动施加约束。因此，在每一时刻，我们都希望向网络提供关于按下键集合的信息，以促进模型训练。
为此，我们在原始数据序列的基础上补充了一种新的映射，称为“开启映射”，如图2a所示。该序列的高度设置为10，因为人类只有十根手指，可在按下下一个键之前持续按住当前的键。

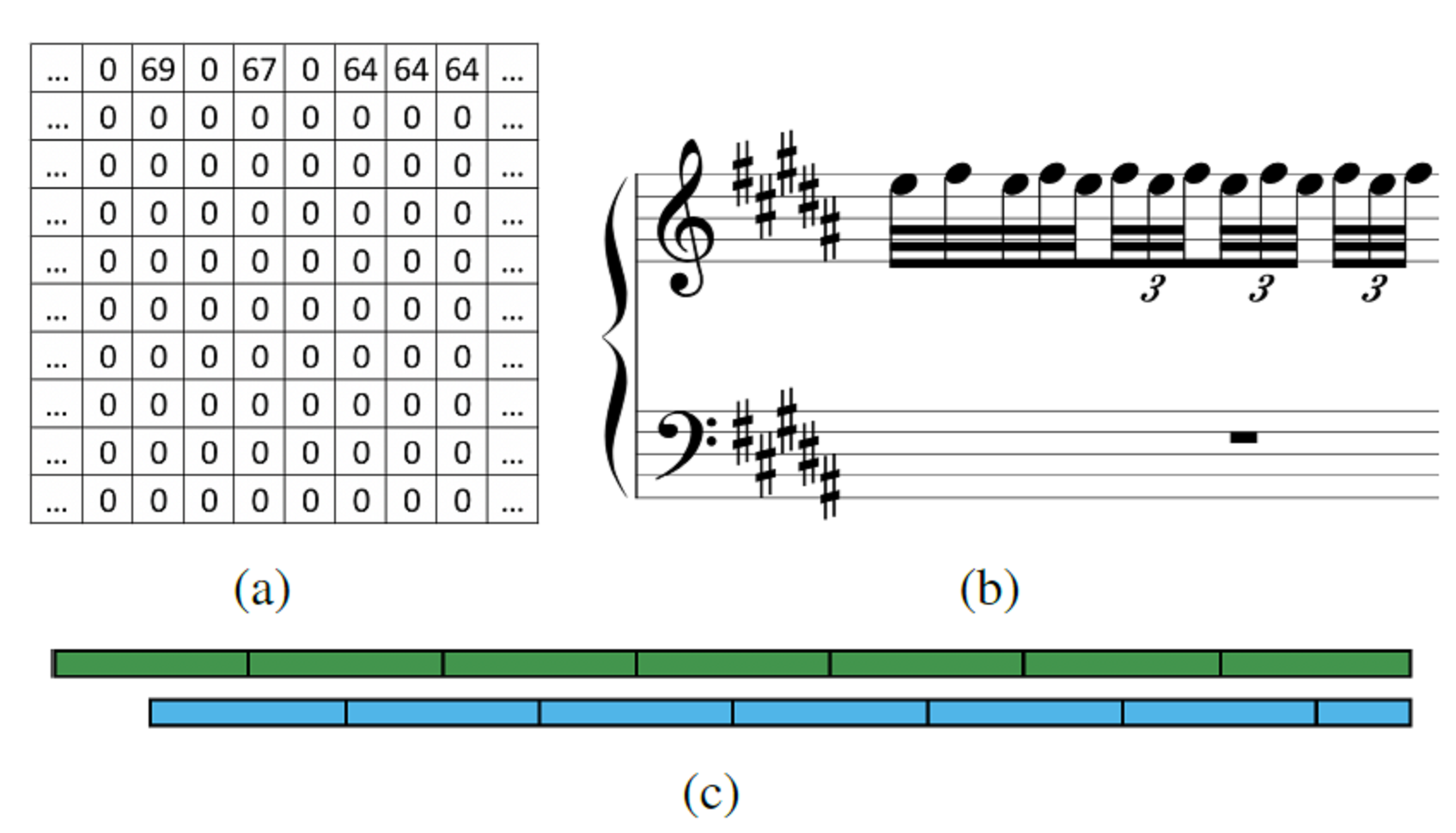
然而，如果我们直接应用此约束，将会出现一个问题。在某些MIDI文件中，踏板效果并非由控制变化消息控制，而是依赖于音符关闭消息的延迟，这通常会导致按下键超过10个。例如，如果钢琴谱中存在如图2b所示的颤音，则该颤音在MIDI文件中将表示为图2c。
同样的问题也可能出现在另外两种情况中。第一种情况是当存在带有乐谱的琶音或华彩段时
第二种情况是在短时间内连续出现多个和弦。这两种情况的原因与带有延迟音符关闭消息的颤音类似。因此，开启键的总数将超过10个。我们设计了一种策略来克服此类问题。
1) 当同一个按下键存在时，若出现热键，则用新信息替换开启映射中的旧键信息。
2) 若出现一个热键或一组热键，并且新增热键后按下键的总数超过10个，则从开启映射中丢弃最旧的键，直到按下键的数量降至10个以下。
3) 若多个按下键将在同一未来时刻被释放，则它们都将从开启映射中移除。

通过这些思路，我们可以克服颤音问题，并解决琶音和持续和弦的问题。为进一步提升性能，我们对模型超参数进行微调。在卷积神经网络模型中，使用丢弃法 [11] 是减少过拟合的有效方法，该方法同样可应用于循环神经网络模型。
应用丢弃法确实进一步降低了模型预测的错误率。通过比较这些结果，我们可以推断：
1) 基于LSTM模型的模型能够从HOT图中学习手部分配。
2) 直接添加时间属性确实有助于提高模型性能，在测试集上的错误率有所降低。
3) 将原始时间属性转换为更直观的表示形式（如算法C中所示），相较于算法B似乎进一步提升了模型性能。

这些规则使得新的开启键序列能够保持在开启映射的10个可用插槽之内。

V. 结论

本文中，我们成功设计了可将单轨MIDI转换为具有双轨的普通钢琴MIDI的算法。提出了一系列针对MIDI文件选择和处理的规则。此外，基于LSTM神经网络，提出了三种手部分配算法。通过训练好的模型实现自动音轨分离，用户可以从单轨MIDI输入直接获得双轨MIDI，且错误率非常低。
未来，我们可能会结合类似[12]中提出的技术，专门处理高复杂度的MIDI文件。我们期望该策略可应用于其他任务，如声音分离或视频恢复。