利用 Lorenz 系统生成神经元发放

在读 LVM （latent variable model）在神经科学 spike 数据上的应用的文献时，我们经常会发现作者喜欢拿 Lorenz Attractor System 来生成 synthetic spiking data，以用于对模型的基础验证。
但是怎么用 Lorenz Attractor系统生成仿真的尖峰数据这个问题一直困扰我，今天在做简单了解后决定记一下，方便后续查找。
这个过程大致可以分为几个步骤：

1. 生成 Lorenz trajectory（通常是一个 三维 的洛伦兹系统轨迹），作为 latents
2. 生成观测矩阵，用于将低维潜变量投影到高维神经元空间
3. 得到高维神经元空间中的发放率
4. 根据发放率经过泊松采样得到尖峰计数

下面对这几个步骤依次做简要解释。

生成 Lorenz trajectory，作为 latents

首先生成lorenz轨迹可以直接调用 dysts.flows.Lorenz 类来实现：

  system = Lorenz()
  system.ic = initial_condition.tolist()  # 设置初始条件
  trace = system.make_trajectory(sequence_length + burn_in)  # 生成轨迹

伪代码如上，设置好初始条件和轨迹长度即可。当然上述代码只能生成一条轨迹，若要生成多条轨迹可以外加一个函数来并行生成多条轨迹，最后返回的是形状为(num_seq, sequence_length, 3)的张量，其中3是洛伦兹系统的维度，num_seq 是轨迹数量，用于作为 latents。

生成观测矩阵

生成一个随机数构成的观测矩阵，示例代码如下所示：

C = torch.randn(n_neurons, latents.shape[-1])  # 随机生成观测矩阵
C /= torch.norm(self.C, dim=1, keepdim=True)   # 归一化

观测矩阵 C 的每一行可以理解该神经元受各 latent 的调控量有多少，或者说各 latent 参与并决定该神经活动的权值有多大。

生成发放率

根据 latents 和 观测矩阵 C 可以得到发放率，示例代码如下：

log_rates = torch.einsum("ij,klj->kli", C, latents) + b.squeeze()
rates = torch.nn.functional.softplus(log_rates, beta=softplus_beta)

首先通过 einsum函数将低维的 latents 活动投影到 C 对应的高维的神经元活动，b可以理解为是基线的发放率；接着通过 softplus 得到真实的发放率。值得说明的是，softplus 在数学上表示为：

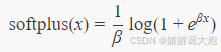
当 x 很大时，输出的结果近似于 x；当 x 很小时，输出的结果近似于 $e^{\beta x}$。这样，当输入较大时，发放率随输入呈线性增长，防止出现输出无限大的情况，当输入较小时，发放率和输入呈指数关系，也符合生物神经元的生理特性（这里的输入指的是神经元的输入突触的加权输入和）。此外，这一公式还可以防止输出的发放率为负数。

生成尖峰计数

由于神经元的发放满足泊松分布，因此由泊松采样即可得到：

  samples = torch.poisson(rates)

总结

总结下来，这个过程就是，先生成 lorenz 轨迹作为 latents，shape 是 (n_sample, seq_length, n_low_dim)；再根据 latents 和观测矩阵 C 生成从低维映射到高维的发放率矩阵（这中间要经过 softplus 变换），shape 是 (n_sample, seq_length, n_neuron)；最后根据 rate 采样得到 spike counts，shape 同样是 (n_sample, seq_length, n_neuron)，只不过每个bin里的数不再代表着该神经元在这个时间bin里的发放率，而是实际采样到的发放的 spike 数量。