代码下载链接:https://gitee.com/flying-wolf-loves-learning/data-structure.git
目录
一、查找的原理
1.1 查找概念
- 设记录表L=(R1 R2……Rn),其中Ri(l≤i≤n)为记录,对给定的某个值k,在表L中确定key=k的记录的过程,称为查找。
- 若表L中存在一个记录Ri的key=k,记为Ri.key=k,则查找成功,返回该记录在表L中的序号i(或Ri 的地址),否则(查找失败)返回0(或空地址Null)。
1.2 查找方法
查找方法有顺序查找、折半查找、分块查找、Hash表查找等等。查找算法的优劣将影响到计算机的使用效率,应根据应用场合选择相应的查找算法。
1.3平均查找长度
对查找算法,主要分析其T(n)。查找过程是key的比较过程,时间主要耗费在各记录的key与给定k值的比较上。比较次数越多,算法效率越差(即T(n)量级越高),故用“比较次数”刻画算法的T(n)。
一般以“平均查找长度”来衡量T(n)。
- 平均查找长度ASL(Average Search Length):对给定k,查找表L中记录比较次数的期望值(或平均值),即:
(1-1)
为查找
的概率。等概率情况下
;
为查找
时key的比较次数(或查找次数)。
1.4顺序表的查找
顺序表,是将表中记录
……
按其序号存储于一维数组空间
记录
的类型描述如下:
typedef struct
{ keytype key; //记录key
…… //记录其他项
} Retype;
顺序表类型描述如下:
#define maxn 1024 //表最大长度
typedef struct
{ Retype data[maxn]; //顺序表空间
int len; //当前表长,表空时len=0
} sqlist;
若说明:sqlist r,则(r.data[1],……,r.data[r.len])为记录表(R1……Rn), Ri.key为r.data[i].key, r.data[0]称为监视哨,为算法设计方便所设。
1.5 顺序表的查找算法及分析
算法思路 设给定值为k,在表(R1 R2……Rn)中,从Rn开始,查找key=k的记录。
int sqsearch(sqlist r, keytype k)
{ int i;
r.data[0].key = k; //k存入监视哨
i = r.len; //取表长
while(r.data[i].key != k) i--;
return (i);
}
设Ci(1≤i≤n)为查找第i记录的key比较次数(或查找次数):
若r.data[n].key = k, Cn=1;
若r.data[n-1].key = k, Cn-1=2;
……
若r.data[i].key = k, Ci=n-i+1;
……
若r.data[1].key = k, C1=n
- 故ASL = O(n)。而查找失败时,查找次数等于n+l,同样为O(n)。
- 对查找算法,若ASL=O(n),则效率是很低的,意味着查找某记录几乎要扫描整个表,当表长n很大时,会令人无法忍受。
1.6 折半查找算法及分析
算法思路
对给定值k,逐步确定待查记录所在区间,每次将搜索空间减少一半(折半),直到查找成功或失败为止。
设两个游标low、high,分别指向当前待查找表的上界(表头)和下界(表尾)。mid指向中间元素。

图片来源于makeru.com 
图片来源于makeru.com
具体代码如下:
int Binsearch(sqlist r, keytype k) //对有序表r折半查找的算法 { int low, high, mid; low = 1;high = r.len; while (low <= high) { mid = (low+high) / 2; if (k == r.data[mid].key) return (mid); if (k < r.data[mid].key) high = mid-1; else low = mid+1; } return(0); }
不失一般性,设表长n=2h-l,h=log2(n+1)。记录数n恰为一棵h层的满二叉树的结点数。得出表的判定树及各记录的查找次数如图所示。

图片来源于makeru.com
1.7 分块查找算法及分析
分块
设记录表长为n,将表的n个记录分成
个块,每块s个记录(最后一块记录数可以少于s个),即:

图片来源于makeru.com 且表分块有序,即第i(1≤i≤b-1)块所有记录的key小于第i+1块中记录的key,但块内记录可以无序。
- 建立索引
- 每块对应一索引项:
- 其中kmax为该块内记录的最大key;link为该块第一记录的序号(或指针)。

图片来源于makeru.com
1.8 总结
- 顺序、折半、分块查找和树表的查找中,其ASL的量级在O(n)~O(log2n)之间。
- 不论ASL在哪个量级,都与记录长度n有关。随着n的扩大,算法的效率会越来越低。
- ASL与n有关是因为记录在存储器中的存放是随机的,或者说记录的key与记录的存放地址无关,因而查找只能建立在key的“比较”基础上。
二、Hash表原理
2.1 Hash表的查找
理想的查找方法是:对给定的k,不经任何比较便能获取所需的记录,其查找的时间复杂度为常数级O(C)。
这就要求在建立记录表的时候,确定记录的key与其存储地址之间的关系f,即使key与记录的存放地址H相对应:
当要查找key=k的记录时,通过关系f就可得到相应记录的地址而获取记录,从而免去了key的比较过程。
这个关系f就是所谓的Hash函数(或称散列函数、杂凑函数),记为H(key)。
它实际上是一个地址映象函数,其自变量为记录的key,函数值为记录的存储地址(或称Hash地址)。
- 不同的key可能得到同一个Hash地址,即当keyl≠key2时,可能有H(key1)=H(key2),此时称key1和key2为同义词。这种现象称为“冲突”或“碰撞”,因为一个数据单位只可存放一条记录。
- 一般,选取Hash函数只能做到使冲突尽可能少,却不能完全避免。这就要求在出现冲突之后,寻求适当的方法来解决冲突记录的存放问题。
根据选取的Hash函数H(key)和处理冲突的方法,将一组记录(R1 R2……Rn)映象到记录的存储空间,所得到的记录表称为Hash表,如图:

图片来源于makeru.com
选取(或构造)Hash函数的方法很多,原则是尽可能将记录均匀分布,以减少冲突现象的发生。以下介绍几种常用的构造方法。
- 直接地址法
- 平方取中法
- 叠加法
- 保留除数法
- 随机函数法
2.2 保留除数法
又称质数除余法,设Hash表空间长度为m,选取一个不大于m的最大质数p,令: H(key)=key%p。
设记录的key集合k={28,35,63,77,105……},若选取p=21=3*7(包括质数因子7),有:
key:28 35 63 77 105 ……
H(key)=key%21: 7 14 0 14 0 ……
使得包含质数因子7的key都可能被映象到相同的单元,冲突现象严重。
若取p=l9(质数),同样对上面给定的key集合k,有:
key:28 35 63 77 105
H(key)=key%19: 9 16 6 1 10
H(key)的随机度就好多了。
2.3 处理冲突的方法
选取随机度好的Hash函数可使冲突减少,一般来讲不能完全避免冲突。设Hash表地址空间为0~m-l(表长为m):

图片来源于makeru.com 冲突是指:表中某地址j∈[0,m-1]中己存放有记录,而另一个记录的H(key)值也为j。
- 处理冲突的方法一般为:在地址j的前面或后面找一个空闲单元存放冲突的记录,或将相冲突的诸记录拉成链表。
- 在处理冲突的过程中,可能发生一连串的冲突现象,即可能得到一个地址序列H1、H2……Hn,Hi∈[0,m-l]。H1是冲突时选取的下一地址,而H1中可能己有记录,又设法得到下一地址H2……直到某个Hn不发生冲突为止。这种现象称为“聚积”,它严重影响了Hash表的查找效率。
- 冲突现象的发生有时并不完全是由于Hash函数的随机性不好引起的,聚积的发生也会加重冲突。
- 还有一个因素是表的装填因子α,α=n/m,其中m为表长,n为表中记录个数。一般α在0.7~0.8之间,使表保持一定的空闲余量,以减少冲突和聚积现象。
2.3 开放地址法
当发生冲突时,在H(key)的前后找一个空闲单元来存放冲突的记录,即在H(key)的基础上获取下一地址:
Hi=(H(key)+di)%m
其中m为表长,%运算是保证Hi落在[0,m-l]区间;
di为地址增量。di的取法有多种:
(1)di=1,2,3,……(m-1)——称为线性探查法;
(2)di=12,-12,22,-22,……——称为二次探查法。
设记录的key集合k={23,34,14,38,46,16,68,15,07,31,26},记录数n=11。
令装填因子α=0.75,取表长m= én/αù =15。
用“保留余数法”选取Hash函数(p=13):
H(key)=key%13
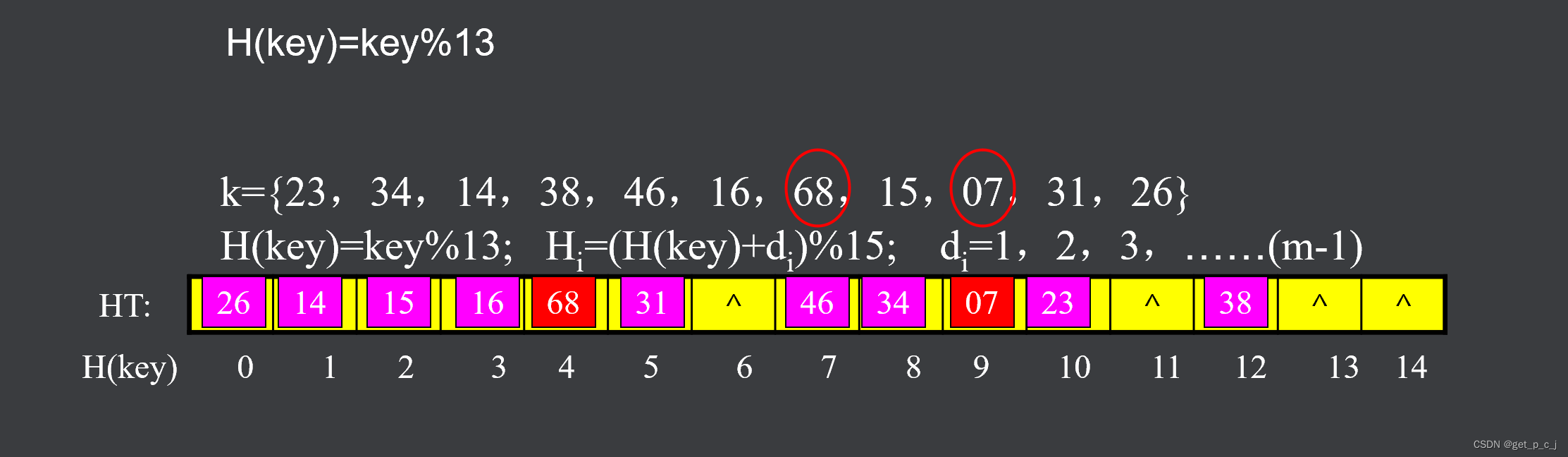
图片来源于makeru.com
2.4 链地址法
发生冲突时,将各冲突记录链在一起,即同义词的记录存于同一链表。
设H(key)取值范围(值域)为[0,m-l],
建立头指针向量HP[m],
HP[i](0≤i≤m-l)初值为空。
设H(key)=key%13
k={ 23,34,14,38,46,
16,68,15,07,31,26 }
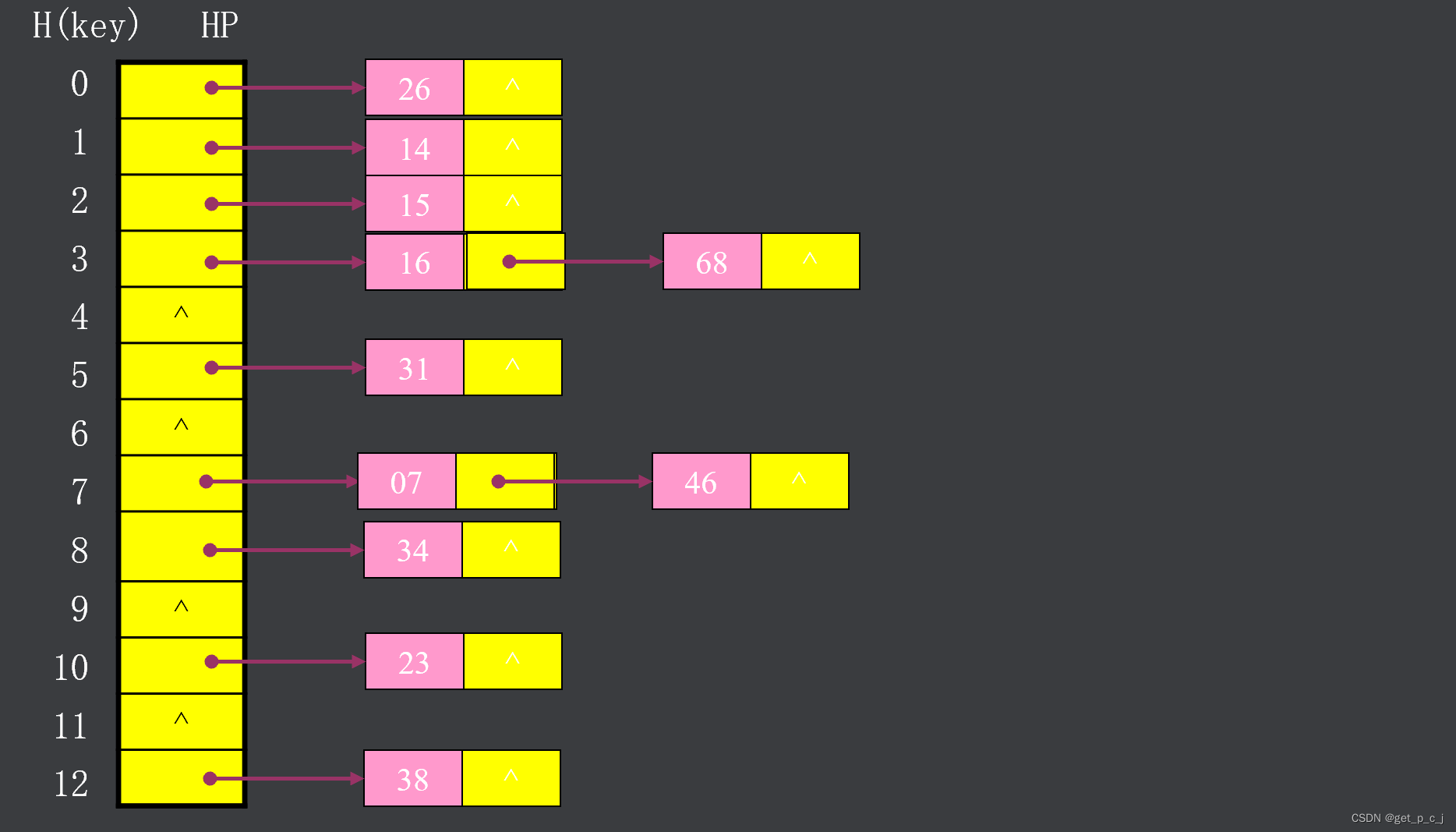
图片来源于makeru.com 链地址法解决冲突的优点:无聚积现象;删除表中记录容易实现。
三、Hash表的实现
3.1 创建
// 定义一个名为hash_create的函数,它返回一个指向hash结构体的指针
hash *hash_create(){
// 声明一个名为HT的指针,用于指向新创建的hash结构体
hash * HT;
// 使用malloc函数为hash结构体分配内存,并将返回的地址赋值给HT
// 这里的(hash *)是强制类型转换,确保malloc返回的void*被正确转换为hash*
if((HT = (hash *)malloc(sizeof(hash))) == NULL){
// 如果内存分配失败(即malloc返回NULL),则打印错误信息
printf("malloc failed!\n");
// 并返回NULL,表示创建失败
return NULL;
}
// 使用memset函数将HT指向的内存区域初始化为0
// 这通常是为了确保hash结构体中的所有成员都被正确地初始化为默认值(对于整数和指针,通常是0)
memset(HT, 0, sizeof(hash));
// 返回新创建的并已经初始化的hash结构体的地址
return HT;
}3.2 插入和查找
插入
// 假设datatype是键的数据类型,hash是哈希表结构体的指针,linklist是链表节点的指针类型
// listnode是链表节点的结构体类型,HT->data是哈希表存储的链表数组,N是哈希表的大小
int hash_insert(hash *HT, datatype key){
// 检查哈希表是否为空
if(HT == NULL){
printf("HT is NULL\n");
return -1; // 返回-1表示哈希表为空,插入失败
}
// 声明两个链表节点的指针,p用于新节点,q用于遍历链表
linklist p, q;
// 为新节点分配内存
if((p = (linklist)malloc(sizeof(listnode))) == NULL){
printf("malloc failed!\n");
return -1; // 返回-1表示内存分配失败
}
// 初始化新节点的key和value(这里value被简单设置为key对N取模的值,可能是哈希值或链表索引)
p->key = key;
p->value = key % N; // 注意:这里的value可能不是真正的值,而是用于链表排序或索引的
p->next = NULL; // 初始化新节点的next指针为NULL
// 计算哈希值,确定在哈希表的哪个位置插入新节点
// 假设HT->data是一个链表数组,其索引由key % N确定
q = &HT->data[key % N]; // q指向对应链表的头部
// 遍历链表,找到新节点应该插入的位置(保持链表有序或按某种规则插入)
// 这里假设链表是按键值key升序排列的
while(q->next && q->next->key < p->key){
q = q->next; // q向后移动,直到找到空位置或遇到比p->key大的节点
}
// 将新节点p插入到链表中的正确位置
p->next = q->next; // 新节点的next指向q原本指向的下一个节点
q->next = p; // q的next指向新节点p
// 插入成功,返回0
return 0;
}
查找
linklist hash_search(hash *HT, datatype key){
// 检查哈希表是否为空
if(HT == NULL){
printf("HT is NULL\n");
return NULL; // 如果哈希表为空,则返回NULL
}
// 声明链表节点的指针p,用于遍历链表
linklist p;
// 计算哈希值,确定在哈希表的哪个位置查找
p = &HT->data[key % N]; // p指向对应链表的头部
// 遍历链表,查找具有给定key的节点
while(p->next && p->next->key != key){
p = p->next; // 如果当前节点的下一个节点存在且key不匹配,则移动到下一个节点
}
// 检查是否找到了匹配的节点
if(p->next == NULL){
// 如果没有找到(即p->next为NULL),则返回NULL
return NULL;
}
else{
// 如果找到了,打印一条消息
printf("found!\n");
}
// 返回找到的节点的指针(注意:是p->next,因为p指向的是链表头部的指针)
return p->next;
}






















 4847
4847

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








