NNDL 作业8 卷积 导数 反向传播

习题5-2 证明宽卷积具有交换性， 即公式(5.13)．

证明rot180(W) ⊗ ~X = rot180(X) ⊗ ~W。

假设输入矩阵X的大小为N×M，滤波器矩阵W的大小为K×L。

1. 定义rot180操作：对于一个矩阵A，rot180(A)的定义是将矩阵A进行180度旋转。其实际操作是将矩阵A沿着水平和垂直中心分别进行翻转得到rotated A。

2. 展开rot180(W) ⊗ ~X，以及rot180(X) ⊗ ~W的计算步骤。

   • 对于rot180(W) ⊗ ~X： 我们首先计算rot180(W)，得到一个大小为K×L的矩阵，记为rotated_W。 然后进行矩阵~X和rotated_W的宽卷积计算，得到结果矩阵C。

   • 对于rot180(X) ⊗ ~W： 我们首先计算rot180(X)，得到一个大小为N×M的矩阵，记为rotated_X。 然后进行矩阵~W和rotated_X的宽卷积计算，得到结果矩阵D。

3. 证明C=D。

   • 对于矩阵C的第i行第j列元素C(i,j)： C(i, j) = ∑(p, q) rotated_W(p, q) * ~X(i-p+1, j-q+1)

   • 对于矩阵D的第i行第j列元素D(i,j)： D(i, j) = ∑(p, q) ~W(p, q) * rotated_X(i-p+1, j-q+1)

4. 证明C和D的每个元素是相等的。

   对C(i,j)和D(i,j)，我们可以发现它们的计算公式非常相似，只是对rotated_W和~X的索引顺序进行了调整。

   结合宽卷积的定义和rot180操作的性质，易得rotated_W和~X的对应关系，使得C(i,j)和D(i,j)中的每一项对应相等。

   所以C=D，即rot180(W) ⊗ ~X = rot180(X) ⊗ ~W。

习题5-4 对于一个输入为100 × 100 × 256的特征映射组， 使用3 × 3的卷积核， 输出为100 × 100 × 256的特征映射组的卷积层， 求其时间和空间复杂度． 如果引入一个1 × 1卷积核， 先得到100 × 100 × 64的特征映射， 再进行3 × 3的卷积， 得到100 × 100 × 256的特征映射组， 求其时间和空间复杂度．

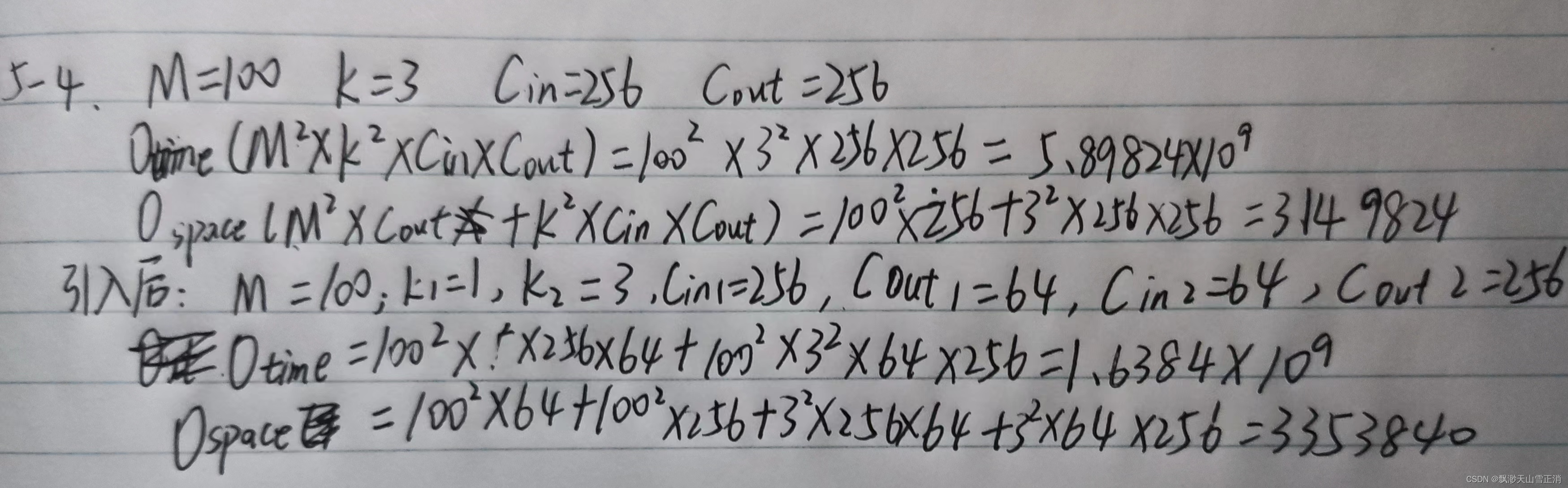
习题5-5 对于一个二维卷积， 输入为3 × 3， 卷积核大小为2 × 2， 试将卷积操作重写为仿射变换的形式． 参见公式(5.45) .

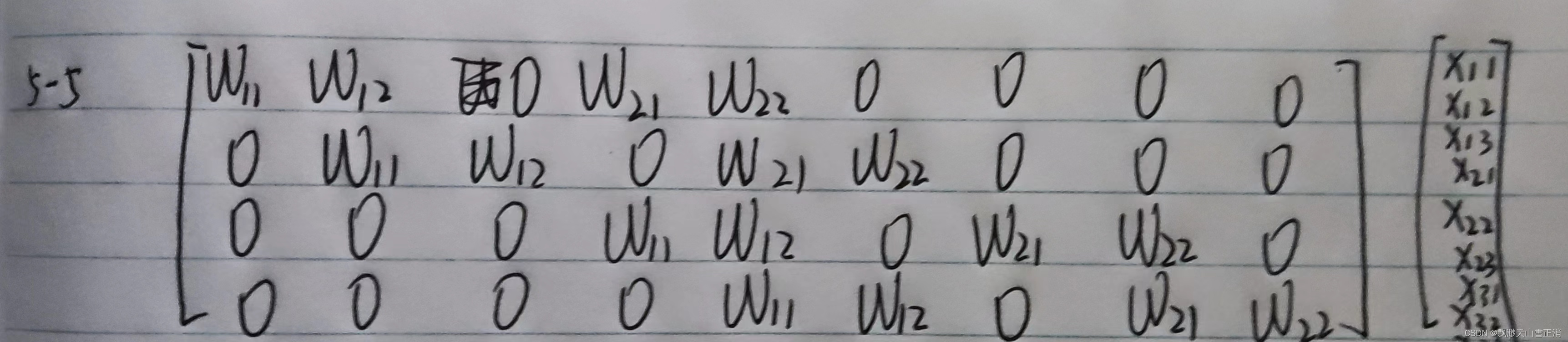
附加题 阅读 “5.3.1 卷积神经网络的反向传播算法”，举例说明推导过程.

卷积神经网络(CNN)反向传播算法推导 - 知乎

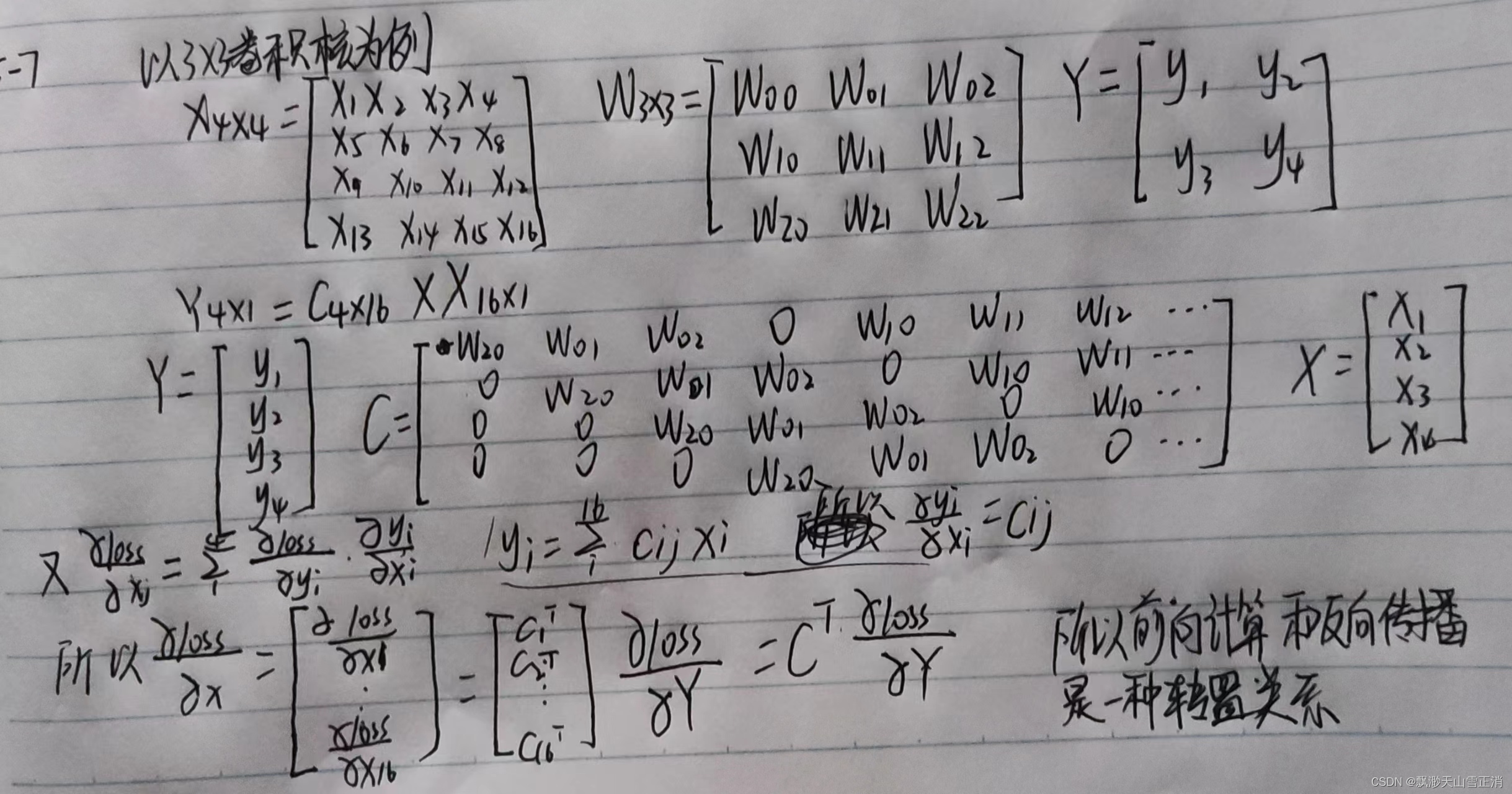
习题 5-7 忽略激活函数， 分析卷积网络中卷积层的前向计算和反向传播（公式(5.39)） 是一种转置关系．

习题5-8 在空洞卷积中， 当卷积核大小为𝐾， 膨胀率为𝐷时， 如何设置零填充𝑃的值以使得卷积为等宽卷积 .

假设卷积层的输入神经元个数为 𝑀 ，卷积大小为 𝐾 ，步长为 𝑆 ，在输入两端各填补 𝑃 个 0 ，那么该卷积层的神输出经元数量为 ：(𝑀 − 𝐾 + 2𝑃)/𝑆 + 1

P=[K+(K-1)*(D-1)-1]/2

化简：P=D*(K-1)/2