＜Uniswap v3 数学洞察＞笔记（part 1）

整理运行后的代码和相关文件，见github：https://github.com/Gogogoforit/Uniswap_V3_Math_Insights_Notes/tree/main/Part%201

1. 重点概要

• 类似Uniswap Analytics[2]和Yewbow[3]这样的工具可以帮助发现产生 LP 费用的交易量。

• 使用循环图这一统计工具（附录中提供的代码），可以识别价格范围的模式，从而帮助找到最小化发散损失（无偿损失）的交易点。

• +/- 84% 的价格边界范围优化了对称的最大范围，来减少在 LP 头寸中使用的资本（提高资本效率）的同时，避免市场价格走出可接受的范围。

2. 这使得如果在随机的时间点退出，而此时 X/ETH 的比率与您最初进入时的比率不匹配，您更有可能发生发散损失（发散损失简单推理见附录）。然而，与此同时，作为 LP，您会从这个发散的山丘中获得费用收益。这是 LP 所面临的主要权衡。

发散损失的简单推导：

以进入时价格为 X:Y=100:1，退出时为 X:Y=120:0.833 为例，起初 20X 能兑换 0.2Y，由于发散损失，在退出时，资产价格损失使得 20X 只能兑换 0.1658Y

3.如何保持在山丘上以避免发散损失？从数学的角度来看，人们的目标是选择一个 X/Y 池，该池具有较高的费用、高交易活动以及重新回到原始价格的高可能性，以便能够平仓 LP 头寸。

4. 在 Uniswap 上进行流动性提供（LPing）的核心要点如下：

1). 确定交易量发生的地点。

2). 找出价格回归到原始比率的地点，以最小化发散损失。我将这个比率称为循环点。

3). 选择一个最佳范围，以最小化资本使用并最大化范围。作为基本策略，我们将通过一些微积分找到，不论随机过程的性质如何，当我们对价格走势不确定时，**+/- 84%** 是我们的上下界限的限制。

5.作为 LP，人们希望最大程度地增加回归/价格回归的机会，以最小化发散损失。这意味着人们从 X/ETH 的某个比率开始，比如 2/1，并希望在未来的某个时间重新回到 2/1。在统计学中，用于发现回归的一个有用工具是查看循环图[5]。这些图允许我们看到系统何时再次回到特定点，比如比率

右侧的循环图捕捉到了这一模式，颜色越黄，点在时间中重新访问的可能性越大。

6. 

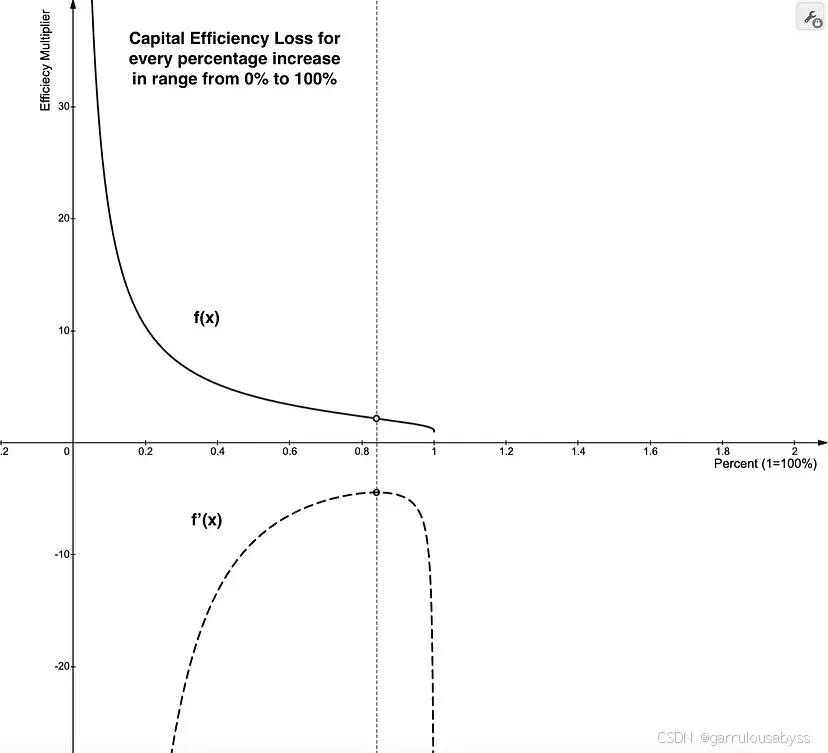
这也意味着，当我们开始增加上下边界以尽可能多地捕获范围时，我们会发现如果我们不确定价格走势，超过 84％ 变得微不足道。对于每超过 1％ 的增加，我们获得的回报越来越少，相反，84％ 成为平衡价格逃离边界和资本效率的 LP 策略的极限。